Оценивание параметров линейной модели множественной регрессии
Модель 1: МНК, использованы наблюдения 1-24
Зависимая переменная: Y
|
|
Коэффициент |
Ст. ошибка |
t-статистика |
P-значение |
|
|
const |
60,4442 |
7,15865 |
8,4435 |
<0,00001 |
*** |
|
X1 |
0,193684 |
0,398708 |
0,4858 |
0,63268 |
|
|
X2 |
-0,0798086 |
0,0720325 |
-1,1080 |
0,28171 |
|
|
X3 |
0,053812 |
0,208385 |
0,2582 |
0,79900 |
|
|
X4 |
0,639778 |
0,170594 |
3,7503 |
0,00136 |
*** |
|
Среднее зав. перемен |
76,08333 |
|
Ст. откл. зав. перемен |
14,58980 |
|
Сумма кв. остатков |
2382,109 |
|
Ст. ошибка модели |
11,19706 |
|
R-квадрат |
0,513441 |
|
Испр. R-квадрат |
0,411008 |
|
F(4, 19) |
5,012443 |
|
Р-значение (F) |
0,006266 |
|
Лог. правдоподобие |
-89,22678 |
|
Крит. Акаике |
188,4536 |
|
Крит. Шварца |
194,3438 |
|
Крит. Хеннана-Куинна |
190,0162 |
Рисунок 1 – Окно с результатами вычислений
Проверка нормальности распределения регрессионных остатков
Для проверки значимости модели и значимости коэффициентов нужно убедиться, что остатки нормально распределены.
:
распределение регрессионных остатков
не отличается от нормального.
:
распределение регрессионных остатков
отличается от нормального.
Рисунок 2 – Гистограмма регрессионных остатков при автоматическом разбиении на интервалы
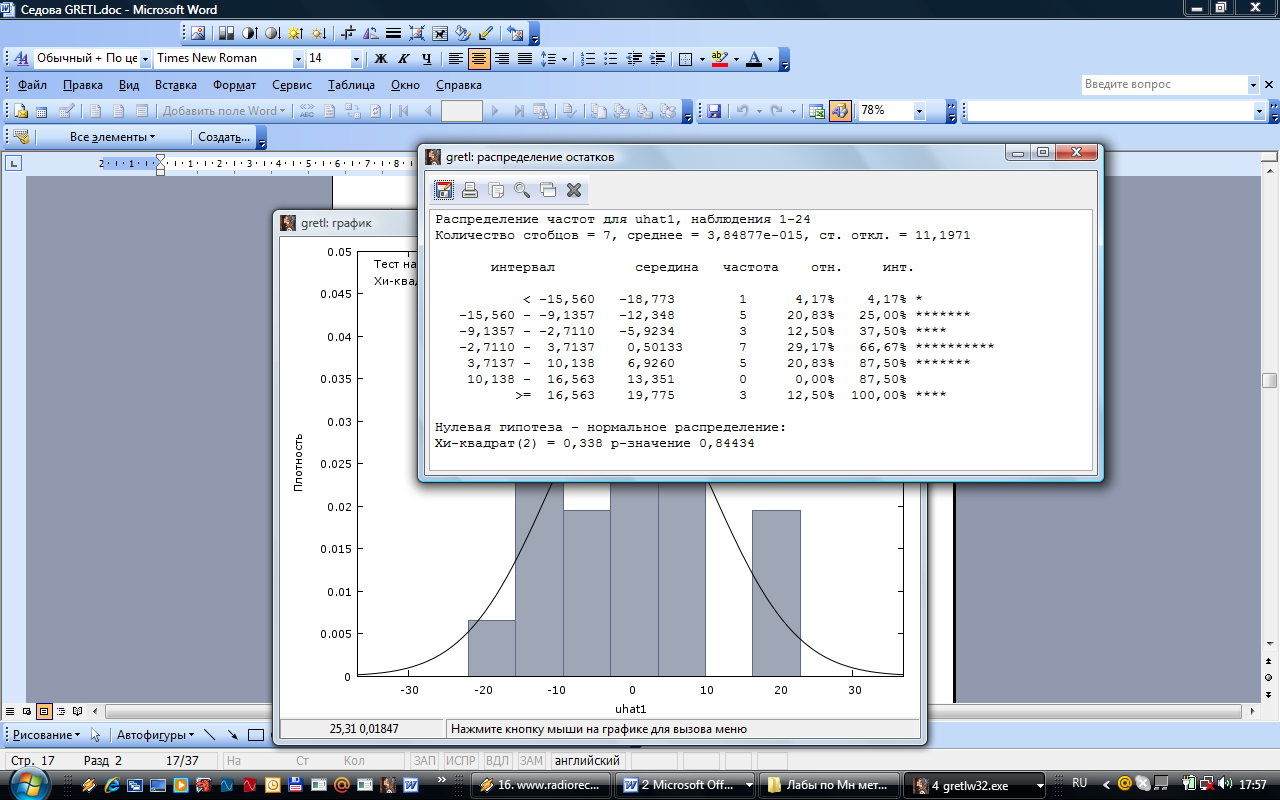
Рисунок 3 – Интервальный ряд абсолютных и относительных частот
Таким образом,
наблюдаемое значение статистики
хи-квадрат составило 0,388 и вероятность
того, что такое значение получилось
случайно, если верна гипотеза
,
составляет всего 0,84. Если принять уровень
значимости
,
то мы должны принять нулевую гипотезу
о нормальном распределении регрессионных
остатков, так как p-значение
0,84>0,05. Известно, что необходимыми
условиями применимости критерия
хи-квадрат является достаточно большой
объем выборки, а также величина абсолютной
частоты в каждом интервале не меньше
5. В нашем случае выборка (N=24)
невелика, и как видно из рисунка 2, не
наблюдается нулевая частота. Поэтому
распределение регрессионных остатков
не отличается от нормального.
Также для проверки согласия распределения с нормальным используются такие критерии, как критерий Дурника-Хансена, критерий Шапиро-Уилка, критерии Лиллифорса и Жака-Бера. Выполним проверку нормальности распределения регрессионных остатков на их основе.
В итоге получаем:
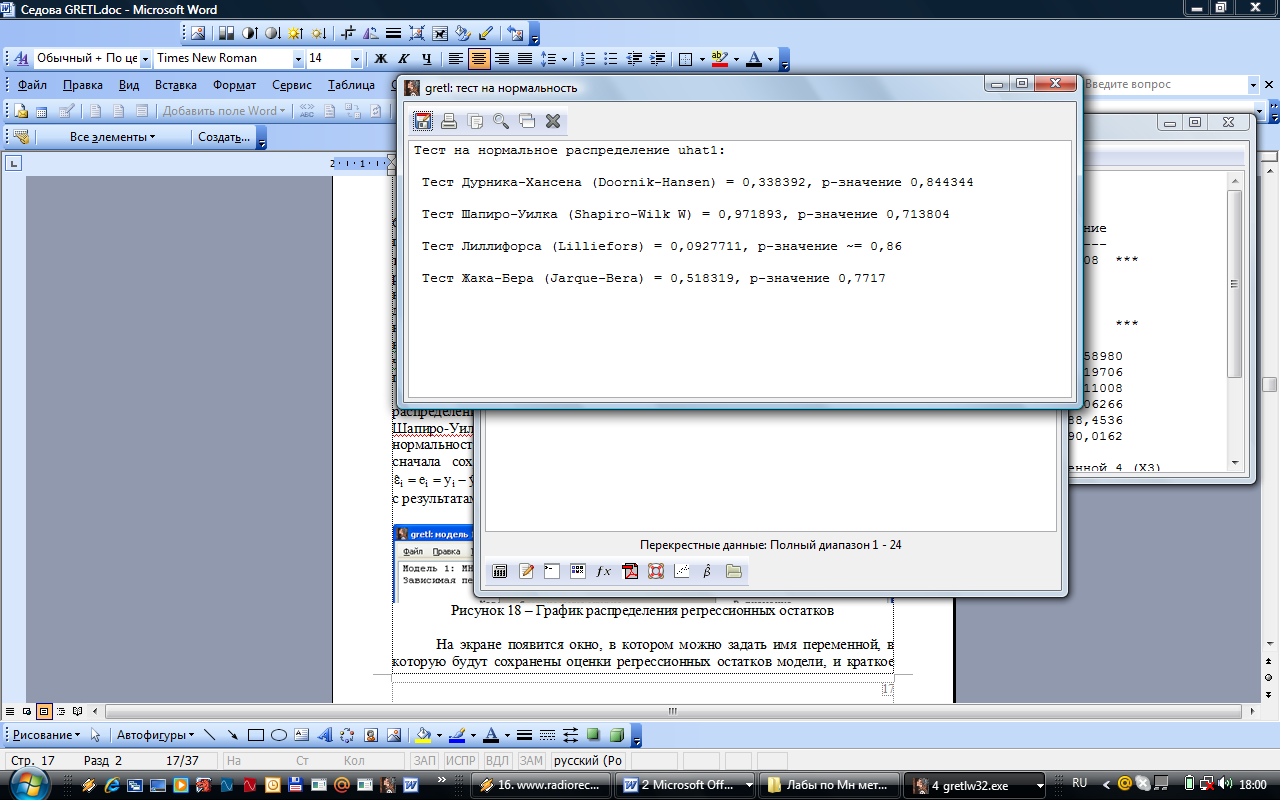
Рисунок 4 – Результаты проверки
По критериям
Шапиро-Уилка, Лиллифорса и Жака-Бера
на уровне значимости
нулевая гипотеза о нормальности
распределения регрессионных остатков
отвергается (достигаемые уровни
значимости равны 0,71,0,86 и 0,77соответственно).