1. Выбор коэффициента размытости из условия минимума оценки квадратического критерия.

Рассмотрим статистику, характеризующую меру близости между и ,

.

Чем меньше , тем точнее оценка аппроксимирует .

Проведём несложные преобразования

.

Третье слагаемое не зависит от коэффициента размытости и является константой, поэтому не влияет на положение минимума .

Тогда критерий оптимальности принимает вид

.

Заметим, что второе слагаемое представляет собой математическое ожидание функции , которое можно оценить по исходной выборке

.

В результате критерий оптимизации (оценка меры близости ) по принимает вид

. (2.6)

В одномерном случае первое слагаемое (2.6) записывается в виде

.

Его значение вычисляется в соответствии со следующими ситуациями:

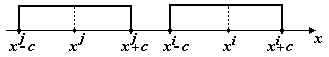
Рис. 2.8. Соотношения между ядерными функциями для варианта .

Рис. 2.9. Соотношения между ядерными функциями для варианта

Приведём правило вычисления интеграла

Второе слагаемое представляется выражением

.

Здесь для устранения смещения анализируемой статистики необходимо принять условие .

Примеры зависимости оценки (2.6) от коэффициента размытости и объёма выборки представлены на рис. 2.10-2.11.

Рис. 2.10. Зависимость критерия (2.6) от коэффициента размытости для нормального закона распределения случайной величины в интервале . Кривая 1 соответствует объёму выборки , кривая 2 – , Кривая 3 - .

Рис. 2.11. Зависимость критерия (2.6) от коэффициента размытости для равномерного закона распределения случайной величины в интервале . Кривая 1 соответствует объёму выборки , кривая 2 - , кривая 2 – , Кривая 3 - .

2. Выбор коэффициента размытости из условия максимума функции правдоподобия

Рассмотрим статистический критерий оптимизации коэффициента размытости вида

, (2.7)

где

.

В предыдущем критерии (2.6) минимальное значение соответствует оптимальному коэффициенту размытости. Для функции (2.7) наоборот, максимальному значению соответствует оптимальной коэффициент размытости.

а б

в г

Рис. 2.12. Зависимость критерия (2.7) от коэффициента размытости для нормального закона распределения случайной величины в интервале . График а соответствует объёму выборки , б - , в – , г - .

а б

в г

Рис. 2.13. Зависимость критерия (2.7) от коэффициента размытости для равномерного закона распределения случайной величины в интервале . График а соответствует объёму выборки , б - , в – , г - .

3. Выбор коэффициентов размытости с помощью метода ближайших соседей

Пусть имеется выборка наблюдений непрерывной случайной величины распределённой с неизвестной плотностью .

Сопоставим каждому элементу обучающей выборки коэффициент размытости . Для этого зафиксируем целую положительную величину , . Определим для каждого наблюдения интервал , таким образом, чтобы в него попало соседних наблюдений. В результате для обучающей выборки получим выборку коэффициентов размытости .

Тогда непараметрическая оценка плотности типа Розенблатта-Парзена (2.2) принимает вид (2.8)

. (2.8)

Рис. 2.14. Непараметрическая оценка плотности вероятности типа (2.8) для равномерного закона распределения случайной величины объёмом в интервале при критерии оптимизации коэффициента размытости . Кривая 1 соответствует оценке плотности вероятности для ступенчатой ядерной функции, кривая 2 - параболической.

Рис. 2.15. Непараметрическая оценка плотности вероятности типа (2.8) для нормального закона распределения случайной величины объёмом в интервале при критерии оптимизации коэффициента размытости . Кривая 1 соответствует оценке плотности вероятности для ступенчатой ядерной функции, кривая 2 - параболической.

Оптимальное количество ближайших соседей можно определить из максимума функции правдоподобия (2.7)

.

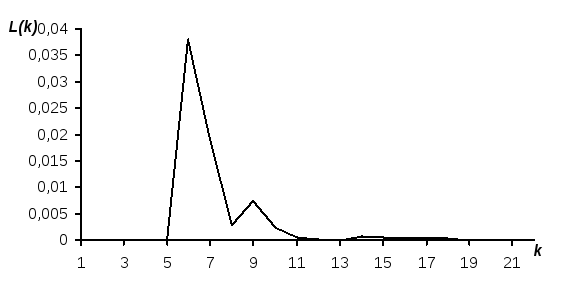
Рис. 2.16. Зависимость критерия от количества ближайших соседей для равномерного закона распределения случайной величины в интервале и объёма выборки .