
- •Модуль 1
- •Преобразуем выражение
- •1. Выбор коэффициента размытости из условия минимума оценки квадратического критерия.
- •2. Выбор коэффициента размытости из условия максимума функции правдоподобия
- •3. Выбор коэффициентов размытости с помощью метода ближайших соседей
- •4. Выбор коэффициента размытости из условия максимума функции правдоподобия для псевдодискретной случайной величины
Преобразуем выражение
![]()
![]()
Рассмотрим отдельно каждое слагаемое:
 ;
;
![]() ;
;
 .
.
Двойную сумму в последнем выражении можно представить в виде
![]()

Рассмотрим последовательно второе и первое их слагаемые



Так как
![]() - статистически независимые наблюдения,
то
- статистически независимые наблюдения,
то
![]() .
Тогда последнее выражение представляется
в виде
.
Тогда последнее выражение представляется
в виде
 .
.
Так как
![]() наблюдения одной и той же случайной
величины, то
наблюдения одной и той же случайной
величины, то
![]() .
Поэтому
.
Поэтому
 .
.
Вынесем выражение
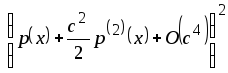
за
знак суммы, как не зависящее от
![]() ,
получим
,
получим
 .
.
При
![]() выражение
выражение
 .
Тогда второе слагаемое окончательно
примет вид
.
Тогда второе слагаемое окончательно
примет вид
 .
.
По аналогии
преобразуем первое слагаемое
![]()

 .
.
Так как
![]() ,
то проводя замену переменных
,
то проводя замену переменных
![]() ,
получим
,
получим

 .
.
Разложим
![]() в ряд Тейлора в точке
в ряд Тейлора в точке
![]()


 .
.
Последнее выражение
при
![]() и
и
![]() принимает вид
принимает вид
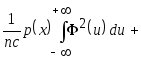

 .
.
В итоге условия сходимости в среднеквадратическом следуют из анализа выражения
![]()

 .
.
Для определения
условий сходимости на всей области
изменения
![]() проинтегрируем полученное асимптотическое
выражение
проинтегрируем полученное асимптотическое
выражение
![]()
 ,
(2.4)
,
(2.4)
где

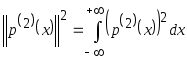 .
.
Заметим,
что величина критерия (2.4) представляет
собой меру близости между искомой
плотностью вероятностей
![]() и её оценкой
и её оценкой
![]() и при конечном объёме выборки в основном
зависит от коэффициента размытости
и при конечном объёме выборки в основном
зависит от коэффициента размытости
![]() и ядерной функции
и ядерной функции
![]() .
Причём зависимость величины критерия
(2.4) от коэффициента размытости имеет
экстремум.
.
Причём зависимость величины критерия
(2.4) от коэффициента размытости имеет
экстремум.
Для
определения минимума критерия (2.4) по
коэффициенту размытости найдём его
производную по
![]() и приравниваем её к нулю
и приравниваем её к нулю

 .
.
Отсюда
 ,
,
 .
.
Тогда оптимальный коэффициент размытости принимает вид
 .
(2.5)
.
(2.5)
При
решении прикладных задач полученным
аналитическим выражением (2.5) для
определения
![]() воспользоваться нельзя, т.к. информация
об второй производной искомой плотности
вероятности неизвестна.
воспользоваться нельзя, т.к. информация
об второй производной искомой плотности
вероятности неизвестна.
Теоретическая значимость полученного результата (2.5) состоит в том, что подтверждается предположение пункта 3 теоремы 2.1
![]() .
.
-
Состоятельность оценки плотности
 следует из
условия равенства её дисперсии нулю,
т.е.
следует из
условия равенства её дисперсии нулю,
т.е.
![]() .
.
Если
![]() является асимптотически несмещённой
оценкой
является асимптотически несмещённой
оценкой
![]() и сходится в среднеквадратическом, то
она обладает свойством состоятельности.
Для доказательства запишем выражение
дисперсии
и сходится в среднеквадратическом, то
она обладает свойством состоятельности.
Для доказательства запишем выражение
дисперсии
![]()
Введём критерий
![]()
![]()
![]()
![]() .
.
Рассмотрим второе слагаемое полученного выражения
![]()
![]() .
.
Далее, с учётом свойства математического ожидания, имеем
![]() .
.
Тогда
дисперсия
![]() представляется в виде
представляется в виде
![]()
![]()
![]() ,
,
где первый член разности определяет сходимость в среднеквадратическом
![]() ,
,
а второй - асимптотическую несмещённость
![]() .
.
Из
результатов теоремы 2.1. сформируем
ограничения, налагаемые на ядерную
функцию и будем называть их в дальнейшем
условиями регулярности
![]() :
:
![]() ,
,
![]() ,
,
 ,
,
 ,
,
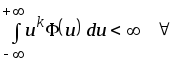
![]() .
.
№16
Пусть дана выборка
![]() статистически независимых наблюдений
случайной величины
статистически независимых наблюдений
случайной величины
![]() ,
распределённой с неизвестным
законом.Методика формирования
регрессионной оценки плотности
вероятности: 1. Разобьём область
определения
,
распределённой с неизвестным
законом.Методика формирования
регрессионной оценки плотности
вероятности: 1. Разобьём область
определения
![]() на
на
![]() непересекающихся интервалов длинной
непересекающихся интервалов длинной
![]() таким образом, чтобы в каждый интервал
попало минимум 2-3 наблюдения. Пусть
таким образом, чтобы в каждый интервал
попало минимум 2-3 наблюдения. Пусть
![]() количество наблюдений в каждом
количество наблюдений в каждом
![]() -м
интервале. 2. Находим оценки вероятностей
попадания наблюдений в каждый
-м
интервале. 2. Находим оценки вероятностей
попадания наблюдений в каждый
![]() -й
интервал по формуле:
-й
интервал по формуле: . 3.
Предполагаем, что в каждом интервале
имеет место равномерный закон распределения
наблюдений. Исходя из этого, находим
высоты полученных прямоугольников.
Площади прямоугольников соответствуют
оценкам вероятности попадания случайной
величины
. 3.
Предполагаем, что в каждом интервале
имеет место равномерный закон распределения
наблюдений. Исходя из этого, находим
высоты полученных прямоугольников.
Площади прямоугольников соответствуют
оценкам вероятности попадания случайной
величины
![]() в j-й интервал. Так как
площадь
в j-й интервал. Так как
площадь
![]() ,
то высота прямоугольников (оценка
плотности вероятности для
,
то высота прямоугольников (оценка
плотности вероятности для
![]() -го
интервала)
-го
интервала)
 . 4.
На основе полученной информации
сформируем статистическую выборку
. 4.
На основе полученной информации
сформируем статистическую выборку
![]() (см. рис. 2.27), где
(см. рис. 2.27), где
![]() - центры введённых интервалов. Из исходной
информации видно, что задача оценивания
плотности вероятности переходит в
проблему восстановления стохастических
зависимостей (рис. 2.28).
- центры введённых интервалов. Из исходной
информации видно, что задача оценивания
плотности вероятности переходит в
проблему восстановления стохастических
зависимостей (рис. 2.28). Рис.
2.27. Графическая интерпретация выборки
для построения регрессионной оценки
плотности вероятностиДля восстановления
зависимости
Рис.
2.27. Графическая интерпретация выборки
для построения регрессионной оценки
плотности вероятностиДля восстановления
зависимости
![]() воспользуемся схемой
воспользуемся схемой Рис.
2.28. Объект исследования При этом
оптимальное решающее правило
Рис.
2.28. Объект исследования При этом
оптимальное решающее правило
![]() в смысле минимума среднеквадратического
критерия является условным математическим
ожиданием
в смысле минимума среднеквадратического
критерия является условным математическим
ожиданием . Плотность
вероятности
. Плотность
вероятности
![]() имеет равномерный закон распределения,
т.к.
имеет равномерный закон распределения,
т.к.
![]() являются центрами равных непересекающихся
интервалов. Исходя из свойства плотности
вероятности
являются центрами равных непересекающихся
интервалов. Исходя из свойства плотности
вероятности
 ,
функция
,
функция
![]() (рис. 2.29).
(рис. 2.29). Рис.
2.29. Вид плотности распределения
вероятностей для величины
Рис.
2.29. Вид плотности распределения
вероятностей для величины
![]() .Подставим
в
.Подставим
в
![]() оценку типа Розенблата-Парзена,
получим:
оценку типа Розенблата-Парзена,
получим:

 ,где
,где
 - выражение математического ожидания
- выражение математического ожидания
![]() с ядерной плотностью, т.к.
с ядерной плотностью, т.к.
![]() обладает всеми свойствами плотности
вероятности (положительная функция и
площадь равна единице). Так как ядерная
функция является симметричной и строится
с центром в ситуации
обладает всеми свойствами плотности
вероятности (положительная функция и
площадь равна единице). Так как ядерная
функция является симметричной и строится
с центром в ситуации
![]() ,
то
,
то .Тогда
.Тогда .В
итоге после сокращений получаем формулу
регрессионной оценки плотности
вероятности
.В
итоге после сокращений получаем формулу
регрессионной оценки плотности
вероятности (2.12) Проверим, обладает оценка (2.12)
основным свойством плотности
вероятности,
(2.12) Проверим, обладает оценка (2.12)
основным свойством плотности
вероятности, . Учитывая,
что площадь ядерной функции равна 1,
имеем
. Учитывая,
что площадь ядерной функции равна 1,
имеем . Если
. Если
![]() - многомерная случайная величина, то
регрессионная оценка плотности
вероятности имеет вид:
- многомерная случайная величина, то
регрессионная оценка плотности
вероятности имеет вид: .
.
№17
Оптимизация регрессионной оценки плотности вероятности по коэффициенту размытости
Преимущество предлагаемых оценок плотности вероятности (2.12), (2.13) заключается:
-
в повышении вычислительной эффективности непараметрических алгоритмов за счёт сжатия исходной обучающей выборки;
-
в упрощении задачи оптимизации коэффициента размытости, например, с помощью метода «скользящего экзамена» по выборке
 при конкретном значении
при конкретном значении
 .
.
Оптимизация многомерной регрессионной оценки плотности вероятности по коэффициенту размытости
В том случае, когда
![]() - многомерная случайная величина
(вектор), то его каждому признаку
соответствует свой коэффициент
размытости. Причем чем больше область
изменения признака, тем больше значения
принимает параметр размытости. Поэтому
для упрощения задачи оптимизации
многомерной оценки плотности вероятности
используют оценки среднеквадратического
отклонения
- многомерная случайная величина
(вектор), то его каждому признаку
соответствует свой коэффициент
размытости. Причем чем больше область
изменения признака, тем больше значения
принимает параметр размытости. Поэтому
для упрощения задачи оптимизации
многомерной оценки плотности вероятности
используют оценки среднеквадратического
отклонения
![]() признаков. В этом случае, коэффициенты
размытости будут иметь вид
признаков. В этом случае, коэффициенты
размытости будут иметь вид
![]() ,
где параметр
,
где параметр
![]() будет общим (см. 2.2.2.2.).
будет общим (см. 2.2.2.2.).
В этом случае многомерная регрессионная оценка плотности вероятности (2.13) принимает вид
 ,
(2.15)
,
(2.15)
Для многомерного случая выражение критерия (2.14) будет иметь вид
 ,
(2.16)
,
(2.16)
из условия минимума которого в режиме
«скользящего экзамена» определяется
оптимальный коэффициент размытости
![]() .
.
№19Методика
проверки гипотезы:Построить эмпирические
функции распределения
![]() и
и
![]() по исходным выборкам
по исходным выборкам
![]() и
и
![]() .
.
 ,
где
,
где

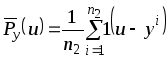 ,
где
,
где

-
Найти максимальное расхождение между эмпирическими функциями распределения
![]() .
.

Рис. 1.9. Иллюстрация к методике проверки
гипотезы
![]()
-
Сравнить полученное максимальное расхождение
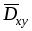 с пороговым
с пороговым
 в соответствии с критерием Смирнова
в соответствии с критерием Смирнова
 ,
(1.15)
,
(1.15)
где
![]() – принятый уровень доверия (риск
отвергнуть гипотезу
– принятый уровень доверия (риск
отвергнуть гипотезу
![]() ,
например,
,
например,
![]() ).
).
Если выполняется условие
![]() ,
тогда гипотеза
,
тогда гипотеза
![]() справедлива, иначе эмпирические законы
распределения различаются значимо.
справедлива, иначе эмпирические законы
распределения различаются значимо.
Рассмотренный критерий Смирнова
обобщает критерий Колмогорова при
проверке гипотезы
![]() о тождественности закона распределения
о тождественности закона распределения
![]() и некоторого теоретического
и некоторого теоретического
![]() (эталонное распределение)
(эталонное распределение)
![]() .
.
Пусть теоретическое распределение
![]() представлено в виде полинома
представлено в виде полинома
![]() ,
где
,
где
![]() его коэффициенты. Эмпирическая функция
распределения
его коэффициенты. Эмпирическая функция
распределения
![]() восстанавливается по выборке
восстанавливается по выборке
![]() ,
извлечённой из генеральной совокупности
,
извлечённой из генеральной совокупности
![]() .
.
Схема действий аналогична проверке
гипотезы
![]() критерием Смирнова.
критерием Смирнова.
Найти максимальное расхождение между
эмпирической функцией распределения
![]() и теоретической
и теоретической
![]()
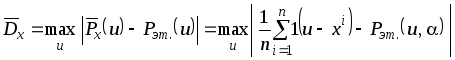 .
.
Сравнить полученный результат
![]() с пороговым значением
с пороговым значением
 ,
(1.16)
,
(1.16)
которое следует из выражения (1.15) при
![]() .
.
Если выполняется условие
![]() ,
тогда справедлива гипотеза
,
тогда справедлива гипотеза
![]() ,
иначе эмпирический закон распределения
не соответствует теоретическому.
,
иначе эмпирический закон распределения
не соответствует теоретическому.
№18
Интегральная оценка плотности вероятности
При ограниченном объёме обучающей выборки оценка плотности вероятности типа Розенблатта-Парзена может оказаться не гладкой, скачкообразной, что негативно сказывается при решении некоторых задач распознавания образов либо автоматической классификации. Возникает проблема сглаживания оценки плотности вероятности таким образом, чтобы не ухудшить (по возможности улучшить) аппрроксимационные свойства оценки. Исходя из этого, была предложена непараметрическая интегральная оценка плотности вероятности [Лапко А.В., 1982].

Рис. 2.17. Графическая интерпретация синтеза интегральной оценки плотности вероятности.
Определим оценку вероятности попадания
случайной величины в интервал
![]()
 ,
,
где
![]() - оценка типа Розенблатта-Парзена (2.2);
- оценка типа Розенблатта-Парзена (2.2);
![]() - плотность вероятности случайной
величины с равномерным законом
распределения на интервале
- плотность вероятности случайной
величины с равномерным законом
распределения на интервале
![]() .
Отсюда интегральная оценка плотности
вероятности в точке
.
Отсюда интегральная оценка плотности
вероятности в точке
![]() представляется статистикой
представляется статистикой
 .
.
№20Методика
проверки гипотезы на основе критерия
Смирнова предесматривает выполнение
след действий:Построить эмпирические
функции распределения
![]() и
и
![]() по исходным выборкам
по исходным выборкам
![]() и
и
![]() .
.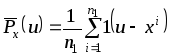 ,
где
,
где

 ,
где
,
где
 Найти
максимальное расхождение между
эмпирическими функциями распределения
Найти
максимальное расхождение между
эмпирическими функциями распределения![]() .
. Рис.
1.9. Иллюстрация к методике проверки
гипотезы
Рис.
1.9. Иллюстрация к методике проверки
гипотезы
![]() Сравнить
полученное максимальное расхождение
Сравнить
полученное максимальное расхождение
![]() с пороговым
с пороговым
![]() в соответствии с критерием Смирнова
в соответствии с критерием Смирнова ,
(1.15)где
,
(1.15)где
![]() – принятый уровень доверия (риск
отвергнуть гипотезу
– принятый уровень доверия (риск
отвергнуть гипотезу
![]() ,
например,
,
например,
![]() ).Если
выполняется условие
).Если
выполняется условие
![]() ,
тогда гипотеза
,
тогда гипотеза
![]() справедлива, иначе эмпирические законы
распределения различаются
значимо.Рассмотренный критерий Смирнова
обобщает критерий Колмогорова при
проверке гипотезы
справедлива, иначе эмпирические законы
распределения различаются
значимо.Рассмотренный критерий Смирнова
обобщает критерий Колмогорова при
проверке гипотезы
![]() о тождественности закона распределения
о тождественности закона распределения
![]() и некоторого теоретического
и некоторого теоретического
![]() (эталонное распределение)
(эталонное распределение)![]() . Пусть
теоретическое распределение
. Пусть
теоретическое распределение
![]() представлено в виде полинома
представлено в виде полинома
![]() ,
где
,
где
![]() его коэффициенты. Эмпирическая функция
распределения
его коэффициенты. Эмпирическая функция
распределения
![]() восстанавливается по выборке
восстанавливается по выборке
![]() ,
извлечённой из генеральной совокупности
,
извлечённой из генеральной совокупности
![]() . Схема
действий аналогична проверке гипотезы
. Схема
действий аналогична проверке гипотезы
![]() критерием Смирнова. Найти максимальное
расхождение между эмпирической функцией
распределения
критерием Смирнова. Найти максимальное
расхождение между эмпирической функцией
распределения
![]() и теоретической
и теоретической
![]()
 . Сравнить
полученный результат
. Сравнить
полученный результат
![]() с пороговым значением
с пороговым значением ,
(1.16)которое
следует из выражения (1.15) при
,
(1.16)которое
следует из выражения (1.15) при
![]() . Если
выполняется условие
. Если
выполняется условие
![]() ,
тогда справедлива гипотеза
,
тогда справедлива гипотеза
![]() ,
иначе эмпирический закон распределения
не соответствует теоретическому.
,
иначе эмпирический закон распределения
не соответствует теоретическому.
№12
