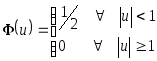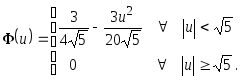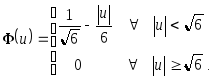Модуль 1

№1 Плотность распределения вероятностей непрерывной случайной величины

Непрерывную случайную величину можно характеризовать не только с помощью функции распределения, но и с помощью плотности распределения вероятностей, которую также называется дифференциальной функцией распределения.

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную функции распределения .

Для описания дискретной случайной величины плотность распределения неприемлема. Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина в некоторой окрестности точки при повторении опытов. После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Основные свойства плотности распределения вероятностей непрерывной случайной величины:

1. Плотность распределения вероятностей неотрицательная функция

.

2. Плотность распределения вероятностей определена на интервале 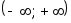, 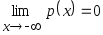и .

3. Площадь под плотностью распределения вероятностей на интервале 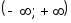равна единице, т.е.

.

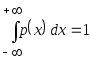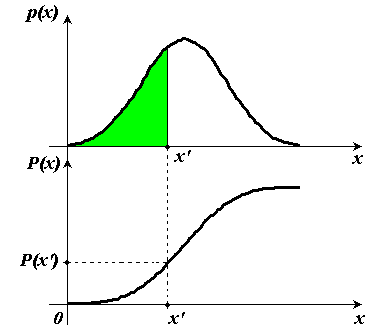
Рис. 1.4. Графическая интерпретация взаимосвязи плотности распределения вероятностей и функции распределения.

Плотность вероятности и функция распределения связаны линейными операторами дифференцирования и интегрирования (рис. 1.4):

, .

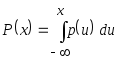Если функция распределения абсолютно непрерывна и дифференцируема при всех значениях аргумента, то её первая производная является плотностью распределения вероятностей .

№2

№3 Гистограммный метод оценивания плотности вероятности

Гистограммный метод один из самых первых и распространённых методов оценки плотности вероятности. Он наиболее удобен в одномерном случае, когда x скаляр.

Пусть дана выборка статистически независимых наблюдений случайной величины , распределённой с неизвестным законом .

Необходимо построить оценку плотности вероятности .

Методика определения оценки плотности вероятности предполагает выполнение следующих действий:

1. Разобьём область определения на равных непересекающихся интервалов длинной таким образом, чтобы в каждый интервал попало минимум 2-3 наблюдения (рис. 2.1).

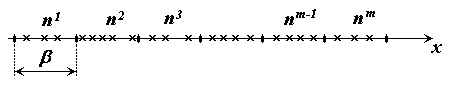
Рис. 2.1. Графическая интерпретация построения оценки плотности вероятности

2. Подсчитать количество наблюдений попавших в каждый -й интервал. Пусть количество наблюдений из исходной выборки в каждом -м интервале.

3. Найти оценки вероятностей попадания наблюдений в каждый -й интервал по формуле

.

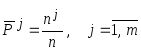4. Предложим, что в каждом интервале закон распределения - равномерный. На плоскости с координатными осями в каждом -м интервале строится прямоугольник площадью и высотой (рис. 2.2)

,

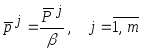являющейся оценкой плотности вероятности.

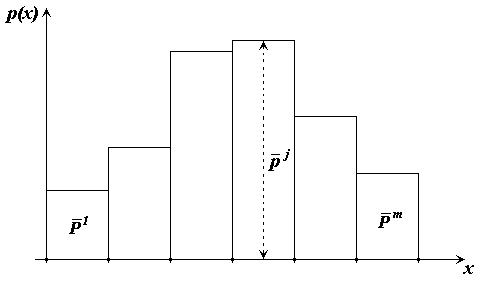
Рис. 2.2. Гистограммная оценка плотности вероятности

В итоге полученную кусочно-постоянную оценку, состоящую из примыкающих друг к другу прямоугольников, называют гистограммой.

№4

№5

№6

Оптимизация непараметрической оценки плотности вероятности типа Розенблатта-Парзена

Выбор коэффициентов размытости из условия минимума статистического критерия составляет одну из основных проблем непараметрических методов оценивания плотности вероятности. Рассмотрим асимптотическое выражение среднеквадратического критерия близости между оценкой и искомой

.

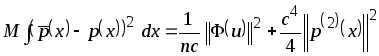Нетрудно заметить, что его значение в основном зависит от коэффициента размытости и вида ядерной функции. Поэтому задача оптимизации сводится к определению наилучшего значения коэффициента размытости и оптимального вида ядерной функции.

№7

Гистограммный метод оценивания плотности вероятности

Гистограммный метод один из самых первых и распространённых методов оценки плотности вероятности. Он наиболее удобен в одномерном случае, когда x скаляр.

Пусть дана выборка статистически независимых наблюдений случайной величины , распределённой с неизвестным законом .

Необходимо построить оценку плотности вероятности .

Методика определения оценки плотности вероятности предполагает выполнение следующих действий:

1. Разобьём область определения на равных непересекающихся интервалов длинной таким образом, чтобы в каждый интервал попало минимум 2-3 наблюдения (рис. 2.1).

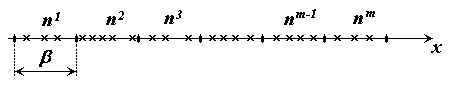
Рис. 2.1. Графическая интерпретация построения оценки плотности вероятности

2. Подсчитать количество наблюдений попавших в каждый -й интервал. Пусть количество наблюдений из исходной выборки в каждом -м интервале.

3. Найти оценки вероятностей попадания наблюдений в каждый -й интервал по формуле

.

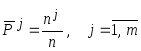4. Предложим, что в каждом интервале закон распределения - равномерный. На плоскости с координатными осями в каждом -м интервале строится прямоугольник площадью и высотой (рис. 2.2)

,

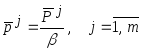являющейся оценкой плотности вероятности.

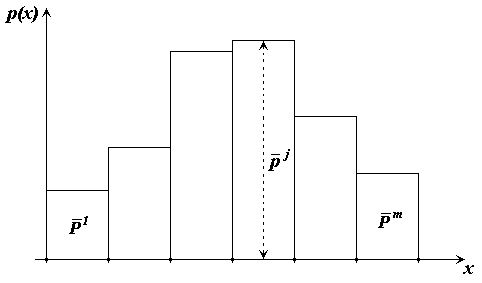
Рис. 2.2. Гистограммная оценка плотности вероятности

В итоге полученную кусочно-постоянную оценку, состоящую из примыкающих друг к другу прямоугольников, называют гистограммой.

№8,10,11,14Исходя из свойств плотности вероятности, площадь под ядерной функцией должна быть равна единицы. Поэтому будем использовать ядерные функции, для которых справедливо соотношение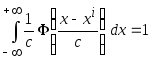 Если - многомерная случайная величина, то непараметрическая оценка плотности вероятности имеет вид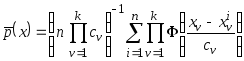. Для трёхмерной случайной величины непараметрическая оценка плотности вероятности принимает вид:

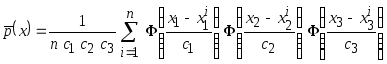. При синтезе многомерной оценки предполагается, что многомерное ядро представимо в виде произведения 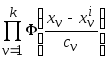. Проверим, обладает ли многомерная оценка (2.3) свойством плотности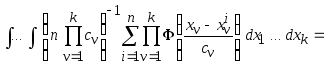

.

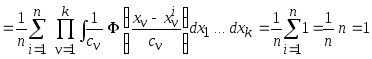Основные виды ядерных функций приведены на рис. 2.4-2.6.

Ступенчатая ядерная функция
Ядерная функция Епанечникова
Треугольная ядерная функция

Ядерная функция – это весовая функция, характеризующая вес по отношению к (аналог меры близости между и ). Коэффициент размытости ядерной функции характеризует её область определения (расплывчатость ядра). При увеличении количества наблюдений значения , т.е. .

Ядерная функция, чтобы сохранить площадь равную 1, должна стремится к дельта-функции

.

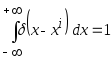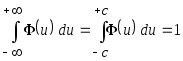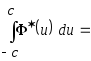
№13Оптимальная ядерная функция представляется в видегде неопределённые множители находятся из ограничений исходной задачи. Подставим в первое ограничение, получим, 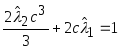. Из симметричности ядерной функции следует, . Далее, с учётом ограничения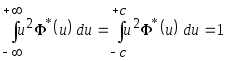, 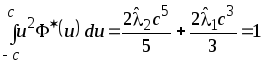. В результате получим уравнения для нахождения параметров . Решая систему уравнений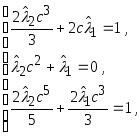получим оптимальную ядерную функцию. На этой основе составляем оптимальную (в смысле минимума среднеквадратического критерия) ядерную функцию Епанечникова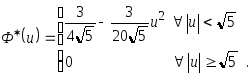 (2.10)

№15 Асимптотические свойства непараметрической оценки плотности вероятности типа Розенблатта-Парзена

Асимптотические свойства показывают поведение рассматриваемой оценки при бесконечном объёме экспериментальных данных (т.е. при ).

Целью исследования асимптотических свойств является проверка сходимости непараметрической оценки с увеличением объёма экспериментальных данных к искомой плотности вероятности

.

Асимптотической сходимостью могут обладать не все оценки плотности вероятности (например, параметрические оценки в общем случае не обладают свойством сходимости).

Теорема 2.1. Пусть: 1) ограничена и непрерывна со всеми своими производными до второго порядка включительно; 2) ядерные функции являются положительными, нормированными и симметричными, а также ; 3) последовательность при , а . Тогда непараметрическая оценка плотности вероятности типа Розенблатта-Парзена обладает свойствами асимптотической несмещённости и состоятельности.

Доказательство.

1. Асимптотическая несмещённость 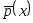, при которой

.

В соответствии со свойством математического ожидания

.

Подставим вместо оценку типа Розенблатта-Парзена

.

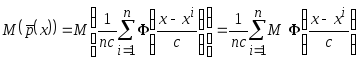Представим математическое ожидание в интегральной форме

.

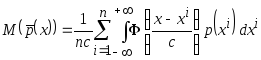Так как наблюдения одной и той же случайной величины, то .

Поэтому

.

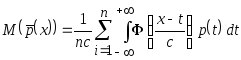Значения не зависят от индекса суммы, что позволяет вынести их за знак суммы. В результате получим

.

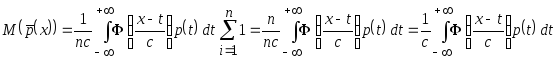Проведём замену переменных в последнем выражении

.

Изменим пределы интегрирования

.

В итоге получим

.

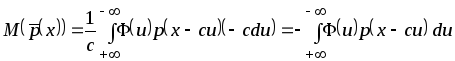Разложим в ряд Тейлора в точке . После очевидных преобразований имеем

.

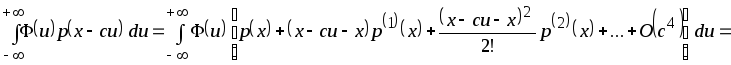
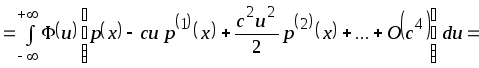
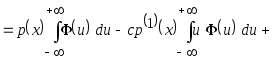
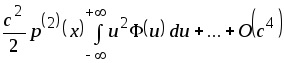Здесь , - первая и вторая производная .

Рассмотрим отдельные части последнего выражения:

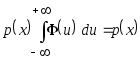, так как ;

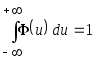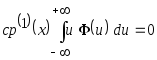, так как 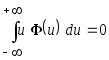. Последнее следует из свойства симметричности ядерной функции. Например, для ядерной функции типа ступеньки имеем .

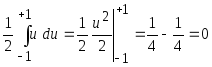Примем 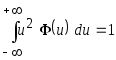, тогда

.

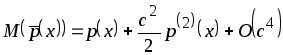Отсюда, при следует свойство асимптотической несмещённости , т.е.

.

2. Сходимость в среднеквадратическом

.