Тема 6. Общее экономическое равновесие и экономическая роль государства Типовые задачи с решениями

№ 1. Первый индивид произвел 200 ед. блага А, а второй – 240 ед. блага В. Предпочтения индивидов относительно данных благ отображаются функциями полезности:

, .

Индивиды договорились о распределении блага А: Q_A1 = 120; Q_А2 = 80.

1. Сколько блага В должен получить 1-й индивид для достижения оптимального по Парето распределения благ?

2. При какой цене блага А рынок обеспечивает оптимальное по Парето распределение, если Р_В = 1?

Решение.

1. Условие оптимального по Парето распределения

.

2. Условие равновесия потребителя

.

Бюджет 1-го индивида 0,8120 + 48 = 144; бюджет 2-го 0,880 + 192 = 256.

Рис. 18. Парето-оптимальность в обмене

№ 2. Кривая производственных возможностей описывается уравнением , а функция общественной полезности: . Определите оптимальные объемы производства каждого блага.

Решение

Производственные возможности выступают в роли бюджетного ограничения при максимизации функции полезности:

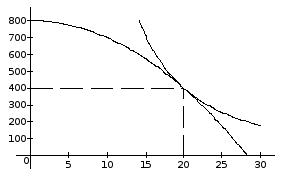
Рис. 19. Оптимум в производстве и обмене

№ 3. Опрос показал, что готовность жильцов трех домов платить за озеленение их двора выражается следующими функциями: P₁ = 80 – Q; P₂ = 60 – Q; P₃ = 40 – Q, где P_i – максимальная сумма денег, которую согласны заплатить жильцы i-го дома за очередное дерево. Общие затраты на озеленение определяются по формуле TC = 10 + 2Q + 0,5Q². Определите Парето-оптимальное число деревьев во дворе дома.

Решение

Оптимальное количество деревьев определяется точкой пересече­ния линий предельных затрат MC = 2 + Q и предельной общественной полезности. Последняя образуется в результате вертикального сложения графиков цены спроса жителей трех домов:

Координаты точки пересечения определяется из равенства: 2 + Q = 140 – 2Q  Q =46. Приравнивание к другим участкам кривой общественной полезности дает решение, не совпадающее с соответствующими интервалами выпуска: 2 + Q = 180 – 3Q  Q = 44,5; 2 + Q = 80 – Q  Q = 39.

Рис. 20. Оптимальный объем выпуска общественного блага

Задачи

№ 1. Первый индивид произвел 120 ед. блага А, а второй – 200 ед. блага В. Предпочтения индивидов относительно данных благ отображаются функциями полезности:

, .

Индивиды договорились о распределении блага А поровну.

1. Сколько блага В должен получить 1-й индивид для достижения оптимального по Парето распределения благ?

2. При какой цене блага А рынок обеспечивает оптимальное по Парето распределение, если Р_В = 1?

№ 2. Для производства двух благ А и В имеется 240 ед. труда и 160 ед. капитала. Технологии производства представлены функциями

; .

При производстве блага А используется 16 ед. капитала, а при производстве блага В – 144 ед. Сколько ед. труда должно быть в отрасли А, чтобы обеспечить эффективность по Парето в производстве?

№ 3. Предпочтения двух потребителей относительно благ А и В представлены функциями полезности: , . Первый потребитель имеет 30 ед. блага А, а второй – 120 ед. блага B. Первый потребитель хочет получить от второго 30 ед. блага B в обмен на определенное количество блага А при Р_В = 3. Какую максимальную цену он может установить на благо А?

№ 4.Предпочтения двух потребителей относительно благ А и В представлены функциями полезности: ,. Первый потребитель имеет 150 ед. блага А, а второй – 120 ед. блага B. Первый потребитель хочет получить от второго 60 ед. блага B в обмен на определенное количество блага А при Р_В = 2. Определите бюджет (ценность имеющихся благ) 1-го потребителя после обмена.

№ 5. В экономике при совершенной производятся два блага по технологиям при L_A + L_B = 500. Функция общественной полезности имеет вид . Если цену блага А принять за 1, то чему должна быть равна цена блага В, чтобы рынок поддерживал в экономике оптимальность по Парето?

№ 6. В экономике при совершенной конкуренции производятся два блага по технологиям, представленным производственными функциями короткого периода: Из общего количества трудовых ресурсов L = 100 в данный момент в производстве блага А используется 80 ед., а в производстве блага В – 20 ед. труда. Какое количество труда перейдет из одной отрасли в другую, если потребительские предпочтения отображаются функцией полезности ?

№ 7. В экономике при совершенной конкуренции производятся два блага по технологиям, представленным производственными функциями короткого периода: . Из общего количества трудовых ресурсов L = 500 в данный момент в производстве блага А используется 176 ед., а в производстве блага В – 326 ед. труда. На сколько единиц изменится объем выпуска блага В, если потребительские предпочтения отображаются функцией полезности ?

№ 8. Опрос показал, что готовность жильцов трех домов платить за озеленение их общего двора выражается следующими функциями: P₁ = 20 – Q; P₂ = 30 – Q; P₃ = 40 – Q, где P_i – максимальная сумма денег, которую согласны заплатить жильцы i-го дома за Q-е дерево; Q – количество посаженных деревьев. Общие затраты на озеленение определяются по формуле TC = 0,125Q². Определите: а) оптимальное число деревьев во дворе трех домов; б) оптимальную сумму затрат на посадку 1-го дерева.

№ 9. Спрос на напитки в жестяных банках отображается функцией Q^D = 200 – 2P. Общие затраты фирмы на выпуск напитков соответствуют функции TC_n = 2Q + 0,25Q², а зависимость затрат на уборку городского мусора от количества купленных напитков выражается функцией TC_u = 0,2Q². На сколько выпуск напитков превышает общественный оптимум, когда расходы на уборку мусора финансирует муниципалитет?

№ 10. На двух взаимосвязанных рынках спрос и предложение отображаются следующими функциями:

1. При каких ценах на обоих рынках одновременно устанавливается равновесие?

2. Является ли равновесие устойчивым?

№ 11. На двух взаимосвязанных рынках спрос и предложение отображаются следующими функциями:

1. При каких ценах на обоих рынках одновременно устанавливается равновесие?

2. Является ли равновесие устойчивым?

№ 12. Готовность абитуриентов платить за учебу в вузах выражается функцией P = 50 – 0,5N, где Р – сумма платы; N – число абитуриентов, тыс. чел. Выраженная в деньгах предельная общественная полезность высшего образования отображается функцией MU = 70 – 0,5N, где MU – предельная общественная полезность. Общие затраты вузов на подготовку специалистов заданы функцией TC = 10N + N².

Определите: а) величину внешнего эффекта подготовки одного специалиста с высшим образованием; б) число студентов, соответствующее максимуму общественной полезности.

Ответы