- •Тема 5. Потоки платежей. Финансовые ренты.
- •Тема 7. Анализ инвестиций в облигации. (конспект лекций)
- •1. Понятия потока платежей и финансовой ренты, их основные параметры
- •2. Классификация финансовых рент
- •3. Обобщающие характеристики потоков платежей, их использование при расчете текущего курса облигаций.
- •3.1. Наращенная сумма постоянных рент постнумерандо и пренумерандо
- •3.2. Современная величина постоянных рент постнумерандо и пренумерандо
- •4. Определение параметров финансовых рент
- •4.1. Определение размера постоянной ренты постнумерандо
- •Формулы для расчета размера платежа постоянных финансовых рент постнумерандо
- •4.2. Определение срока постоянной ренты постнумерандо
- •Формулы для расчета срока постоянных рент постнумерандо
- •4.3. Определение процентной ставки финансовой ренты приближенным методом
- •5. Конверсия финансовых рент
- •5.1. Простые конверсии
- •5.2. Изменение условий ренты
- •5.3. Консолидация рент
- •Ответы к задачам для самостоятельного решения
- •Тестовые задания
- •Коэффициенты наращения годовой ренты
- •Коэффициенты приведения годовой ренты
- •Литература
4.2. Определение срока постоянной ренты постнумерандо
В таблице 2 приведены формулы для расчета срока постоянных рент постнумерандо. Они выводятся из формул (3.1) – (3.21).
Пример 7. Какой необходим срок для накопления 100000 руб. при условии, что в конце каждого месяца вносится 1000 руб., а на взносы начисляются проценты по сложной ставке 25% годовых?
|
Имеем: S = 100000 руб. Rp = 1000 руб. р = 12 ic = 0,25 |
Решение: Так как рента срочная, постнумерандо, проценты начисляются один раз в год, то срок ренты находится по формуле (4.5).
|
|
n = ? |
Годовая сумма платежей: R = Rp p = 1000 12 = 12000 руб. Срок:
|
Так как взносы ежемесячные, переведем дробную часть решения в месяцы.
0,7356 года = 0,7356 12 мес. = 8,8272 мес. < 9 мес.
Полученный результат говорит о том, что после внесения очередного взноса через 4 года и 9 месяцев накопленная сумма впервые превысит нужную сумму в размере 100000 руб.
Следует отметить,
что мы неявно предполагаем, что при
закрытии счета в указанный момент банк
за каждый месяц неполного пятого года
начислит проценты по сложной ставке
![]() за
месяц.
за
месяц.
В нашем примере это составит 1,88% в месяц.
Проверим правильность решения. При ставке 1,88% в месяц за 57 месяцев (4 года 9 месяцев) и ежемесячной выплате 1000 руб. наращенная сумма составит:
![]() руб.
руб.
Задача для самостоятельного решения
7. Определите срок, за который сумма фонда составит 100 тыс. руб., если в фонд вносится по 10 тыс. руб. в конце каждого года и на них ежеквартально начисляются проценты по сложной ставке 8% годовых.
Таблица 2
Формулы для расчета срока постоянных рент постнумерандо
|
Количество платежей в году |
Количество начислений процентов в году |
Сроки платежей |
|
|
S |
A |
||
|
p = 1 |
m = 1 |
|
|
|
годовая рента |
m 1 |
|
|
|
р 1 |
m = 1 |
(4.5) |
|
|
срочная рента |
m =p |
|
|
|
|
m p |
(4.9) |
(4.10) |
4.3. Определение процентной ставки финансовой ренты приближенным методом
В отличие от размера платежа и срока ренты процентная ставка не может быть выражена в явной форме. Поэтому для ее нахождения используются приближенные методы.
Чаще всего используют метод линейной интерполяции.
Для нахождения
приближенного значения годовой сложной
ставки iс,
если известны срок ренты и коэффициент
наращения
![]() ,
применяется следующая интерполяционная
формула:
,
применяется следующая интерполяционная
формула:
![]() ,
(4.11)
,
(4.11)
где
![]() и
и
![]() — верхнее и нижнее значения процентной
ставки, между которыми находится искомое
значение ic.
— верхнее и нижнее значения процентной
ставки, между которыми находится искомое
значение ic.
Эти два значения находятся путем подбора так, чтобы было sн < s < sв.
Здесь s
— коэффициент наращения, для которого
определяется размер ставки ic;
![]() —
коэффициенты наращения для верхнего и
нижнего значений процентной ставки
—
коэффициенты наращения для верхнего и
нижнего значений процентной ставки
![]() и
и
![]() .
.
Если известен
коэффициент приведения ренты
![]() ,
то применяется формула
,
то применяется формула
![]() ,
(4.12)
,
(4.12)
где а — коэффициент приведения, для которого определяется размер ставки ic;
ан,
ав
— коэффициенты приведения для верхнего
и нижнего значений процентной ставки
![]() и
и
![]() .
.
Вычисления по формулам (4.11) и (4.12) могут быть проделаны многократно до получения требуемой точности.
Пример 8. Планируется вносить в банк в течение семи лет в конце каждого года по 10000 руб. Какова должна быть годовая ставка сложных процентов, чтобы к концу срока было накоплено 100000 руб.?
|
Имеем: S = 100000 руб. R = 10000 руб. n = 7 |
Решение:
|
|
ic - ? |
2.
Выберем значения
Для этих значений ставок находим коэффициенты наращения sн и sв. |
Так как рента годовая, постнумерандо, проценты начисляются один раз в год, то коэффициент наращения определяется по формуле:
![]() .
(4.13)
.
(4.13)
Для нижнего значения предполагаемой ставки коэффициент наращения равен по формуле (4.13):
![]() .
.
Для верхнего значения предполагаемой ставки коэффициент наращения равен по формуле (4.13):
![]() .
.
Отсюда ic определяем по формуле (4.11):
![]() или 11,709%.
или 11,709%.

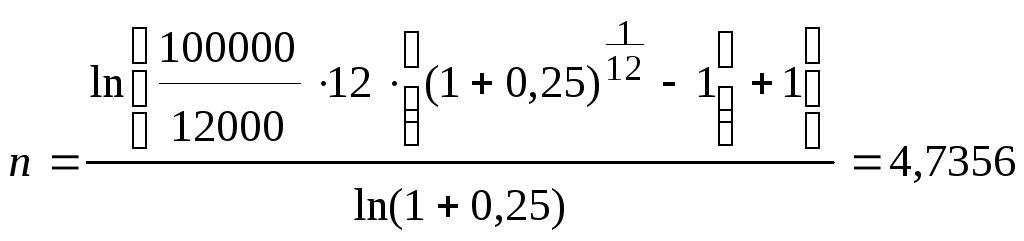 года.
года. (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4)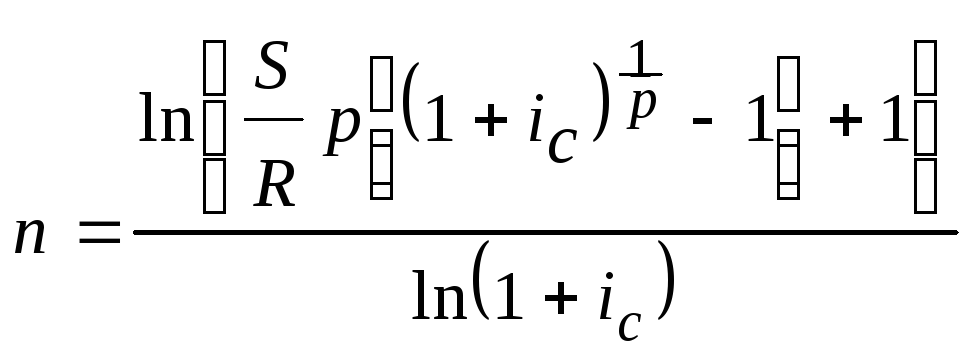
 (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8)