
- •Свойства прообразов и образов
- •Обратная функция.
- •Примеры
- •Эквивалентные определения
- •Примеры
- •Примеры
- •Суперпозиция функций (сложная функция).
- •Определение
- •Свойства композиции
- •Дополнительные свойства
- •Счетные и несчетные множества.
- •Свойства отношения равномощности.
- •Свойство полноты множества вещественных чисел.
- •Плотность множества рациональных чисел в r.
- •Свойства точных границ.
- •Последовательности.
- •Числа x1,x2,…,xn – члены последовательности.
- •Лемма о вложенных отрезках. (Принцип Коши-Кантора)
- •Предел последовательности.
- •Свойства пределов числовых последовательностей.
- •Предел и алгебраические операции.
- •Предельный переход в неравенствах.
- •Бесконечно малые последовательности (величины).
- •Основные свойства б.М. Последовательностей.
- •Бесконечно большие последовательности (величины).
- •Расширение понятие предела.
- •Основные свойства бесконечно больших последовательностей.
- •Связь между бесконечно малыми и бесконечно большими последовательностями.
- •Арифметические свойства предела. (Бесконечно большие последовательности и арифметические операции)
- •Вопросы существования пределов.
- •Свойства фундаментальной последовательности.
- •Монотонные последовательности.
- •Число е.
- •Предел подпоследовательности сходящейся последовательности.
- •Вычисление пределов некоторых последовательностей.
Предел последовательности.
Если изобразить
члены последовательности
![]() точками
на числовой оси, то можно заметить, что
с ростом n члены последовательности xn
становятся ближе к 1 и величина|xn-1|
становится все меньше.
точками
на числовой оси, то можно заметить, что
с ростом n члены последовательности xn
становятся ближе к 1 и величина|xn-1|
становится все меньше.
Определение 1
(аналитическое).
Число а
называется пределом числовой
последовательности {xn},
если для любого сколь угодно малого
положительного числа
можно указать такой номер N,
что все члены xn
последовательности, у которых номер
n>N,
удовлетворяют неравенству: ![]() (2)
(2)
![]()
![]() (отрицание)
(отрицание)
Неравенство (2) равносильно двойному неравенству:
-<xn-a< (если n>N), или а-<xn<а+ (если n>N) (3)
Определение 2 (геометрическое). Число а называется пределом числовой последовательности {xn}, если для каждой окрестности точки а найдется такой номер N, что для всех номеров n>N члены последовательности принадлежат этой окрестности.
![]() ,
,
![]()
Если последовательность имеет предел, то она называется сходящейся. В противном случае – расходящейся.
Примеры. 1)
![]()
![]()
Докажем, что
![]()
![]()
Возьмем N=![]() +1,
тогда N>
+1,
тогда N>![]() .
.
![]()
![]()
([а] - целая часть числа а – наибольшее целое число, не превосходящее а. Например:
![]() )
)
2) Покажем, что
![]() .
.
Докажем, что
![]()
![]()
![]()
![]()
Возьмем N=![]() +1,
тогда N>
+1,
тогда N>![]() .
.
![]()
![]()
3) Доказать, что число (-1) не является пределом последовательности xn=(-1)n.
Доказательство.
Отрицание:
![]()
В нашем случае
![]()
![]()
Т.о. для 0=![]()
![]()
4) Последовательность
называется постоянной,
если все ее члены одинаковы, т.е. xn=a
![]() n=1,2,3,.. Предел
постоянной последовательности
n=1,2,3,.. Предел
постоянной последовательности
![]() =a.
=a.
Свойства пределов числовых последовательностей.
Определение.
Числовая
последовательность {xn}
называется ограниченной,
если
![]() (т.е. множество значений {xn}
ограничено).
(т.е. множество значений {xn}
ограничено).
Последовательность
ограничена
сверху, если
![]()
Последовательность
ограничена
снизу, если
![]()
Теорема (об ограниченности сходящейся последовательности). Сходящаяся последовательность ограничена.
Доказательство.
Пусть xn→a.
Покажем , что
![]() .
.
![]()
![]()
Возьмем =1,
тогда
![]()
![]()
![]()
Положим
С=max{1+a,x1,…,xN}
xn<N
![]() ч.т.д.
ч.т.д.
Предел и алгебраические операции.
Пусть даны две последовательности {xn}и {уn}.
{xn+уn}: x1+y1,x2+y2,… - сумма последовательностей {xn}и {уn}.
{xnуn}: x1y1,x2y2,… - произведение последовательностей {xn}и {уn}.
![]() - отношение, {xn}-
произведение последовательности на
число.
- отношение, {xn}-
произведение последовательности на
число.
Теорема 1.
Пусть даны последовательности {xn}и
{уn}
и
![]() =а,
=а,
![]() =b,
тогда сумма {xn+уn}
также является сходящейся и
=b,
тогда сумма {xn+уn}
также является сходящейся и
![]() =a+b.
=a+b.
Доказательство.
Оценим
![]()
Т.к.
![]() =а,
то
=а,
то
![]()
![]() ,
,
Т.к.
![]() =b,
то
=b,
то
![]()
![]()
Положим
![]() N=max(N1,N2):
N=max(N1,N2):![]()
![]() и
и
![]() .
.
Следовательно,
![]()
![]() ,
т.е.
,
т.е.
![]() =a+b ч.т.д.
=a+b ч.т.д.
Теорема 2.
Пусть даны последовательности {xn}и
{уn}
и
![]() =а,
=а,
![]() =b,
тогда произведение {xnуn}
также является сходящейся и
=b,
тогда произведение {xnуn}
также является сходящейся и
![]() =ab.
=ab.
Доказательство.
![]()
Т.к. {xn} сходящаяся, то она ограничена. Следовательно,
![]()
Подберем с таким
образом, чтобы
![]()
Т.к.
![]() =а,
то
=а,
то
![]()
![]()
Т.к.
![]() =b,
то
=b,
то
![]()
![]()
Положим
![]() N=max(N1,N2):
N=max(N1,N2):![]()
![]() и
и
![]() .
.
Тогда
![]() ,
т.е.
,
т.е.
![]() =ab ч.т.д.
=ab ч.т.д.
Следствие из теоремы 2.
![]() - т.е. константу
можно выносить за знак предела.
- т.е. константу
можно выносить за знак предела.
(Доказательство. Следует из свойства 2 при {уn}=.)
Теорема 3.
Если
![]() =b≠0,
то
=b≠0,
то
![]() - оценка снизу для yn.
- оценка снизу для yn.
Более того, для
указанных n,
если b>0,
то yn>![]() ,
если же b<0,
то yn<
,
если же b<0,
то yn<![]() .
.
Таким образом, начиная с некоторого номера yn сохраняет знак b.
Доказательство.
Т.к.
![]() =b,
то для
=b,
то для
![]()
![]()
С другой стороны
![]()
Получаем
![]() ,
отсюда
,
отсюда
![]() - доказали 1-ю часть.
- доказали 1-ю часть.
С другой стороны,
неравенство
![]() эквивалентно
двум неравенствам:
эквивалентно
двум неравенствам:
b-![]() <yn<b+
<yn<b+![]() ,
n>N
,
n>N
Тогда, если b>0,
то
![]() =
b-
=
b-![]() <yn,
n>N
<yn,
n>N
Если b<0,
то yn<b+![]() =b-
=b-![]() ,
n>N
– доказано 2-е утверждение. Ч.т.д.
,
n>N
– доказано 2-е утверждение. Ч.т.д.
Теорема 4. Пусть
даны последовательности {xn}и
{уn}.
Пусть
![]() =а.
Пусть все значения переменной уn
отличны от нуля и
=а.
Пусть все значения переменной уn
отличны от нуля и
![]() =b
(b≠0),
тогда частное {
=b
(b≠0),
тогда частное {![]() }
также является сходящейся и
}
также является сходящейся и
![]() .
.
Доказательство.
![]() .
Покажем, что
.
Покажем, что
![]() .
.
![]() (1).
(1).
По предыдущему
утверждению,
![]()
![]() (2)
(2)
По (1) и (2)
![]()
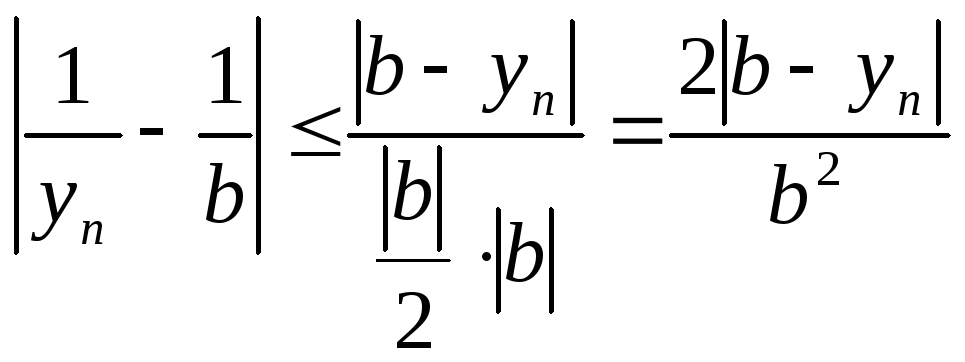
Т.к.
![]() =b,
то
=b,
то
![]()
![]()
Положим
![]() N=max(N1,N2):
N=max(N1,N2):![]()
![]() . Ч.т.д.
. Ч.т.д.
Утверждение (или
задача?). Пусть
даны последовательности {xn}и
{уn}
и
![]() =а,
=а,
![]() =b,
тогда разность {xn-уn}
также является сходящейся и
=b,
тогда разность {xn-уn}
также является сходящейся и
![]() =a-b.
=a-b.
Доказательство.
Оценим
![]() .
Далее аналогично сумме: Т.к.
.
Далее аналогично сумме: Т.к.
![]() =а,
то
=а,
то
![]()
![]()
Т.к.
![]() =b,
то
=b,
то
![]()
![]()
Положим
![]() N=max(N1,N2):
N=max(N1,N2):![]()
![]() и
и
![]() .
.
Следовательно,
![]()
![]() ч.т.д.
ч.т.д.
