13) Криптосистема Эль-Гамаля.

О чём речь:

Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом,основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи. Схема Эль-Гамаля

лежит в основе стандартов электронной цифровой подписи в США и России (ГОСТ Р 34.11-94).

Схема была предложена Тахером Эль-Гамалем в 1984 году. Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана.

Что к чему:

1. Генерируется случайное простое число  длины 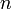 битов.

2. Выбирается произвольное целое число , являющееся первообразным корнем по модулю .

3. Выбирается случайное целое число  такое, что .

4. Вычисляется .

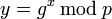5. Открытым ключом является тройка , закрытым ключом — число .

Сообщение  шифруется следующим образом:

1. Выбирается сессионный ключ — случайное целое число  такое, что 

2. Вычисляются числа  и .

3. Пара чисел  является шифротекстом.

Нетрудно видеть (хер знает, может и не трудно, но не вникать в смысл этой фразы), что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения M вдвое.

14) Криптосистема Диффи-Хелмана.

О чём речь:

Алгоритм Диффи — Хеллмана (англ. Diffie-Hellman, DH) — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания, но защищённый от подмены, канал связи. Этот ключ может быть использован для шифрования дальнейшего обмена с помощью алгоритма симметричного шифрования.

Что к чему:

Предположим, что обоим абонентам известны некоторые два числа g и p (например, они могут быть «зашиты» в программное обеспечение), которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение A = g^amod p и пересылает его второму, а второй вычисляет B = g^bmod p и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе, первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение B^amod p = g^abmod p, а второй абонент на основе имеющегося у него b и полученного по сети Aвычисляет значение A^bmod p = g^abmod p. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: K = g^abmod p. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления g^abmod p по перехваченным g^amod p и g^bmod p, если числа p,a,bвыбраны достаточно большими.