1.3.4. Канонические схемы Кауэра

1-ая схема Кауэра

Такая схема называется лестничной или цепной схемой. Сопротивление удобно записать в виде лестничной или цепной дроби:

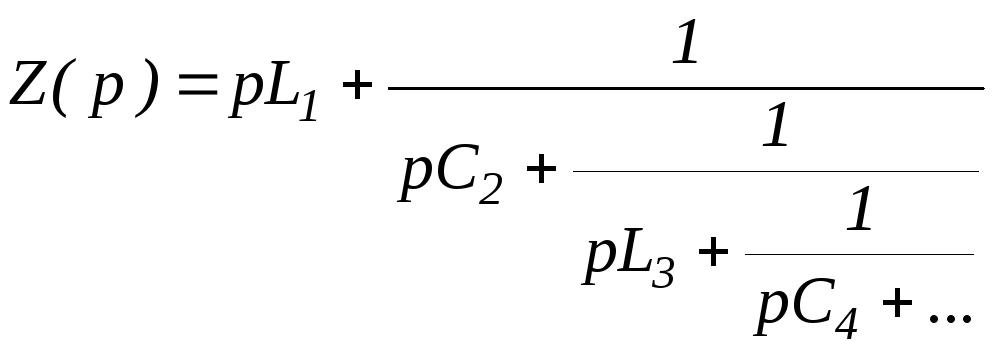
Класс ДП определяют первый и последний элемент (если есть оба элемента, то класс ДП

∞-∞; нет ни одного элемента- 0- 0).

Количество элементов соответствует старшей степени полинома (на единицу больше числа резонансных частот). В частном случае, если мало элементов, то эта схема может совпадать со схемами Фостера. Множитель также определяется при устремлении ω→∞.

Например: Класс ДП 0 – 0 и ДП имеет три резонансных частоты (4 элемента).

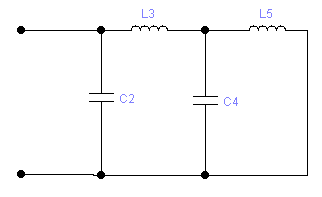
X(ω)

0 ω₂ ω₃ ω₄ ω

2- ая схема Кауэра

Первый и последний элементы определяют класс ДП.

Одну и ту же функцию сопротивления реактивного ДП можно получить различными схемами, например, одной из четырех выше описанных. Тогда эти схемы называются эквивалентными (их сопротивление одинаково при любой частоте).

1.3.5. Понятие о синтезе электрических цепей

В теории цепей синтез – процедура проектирования электрической цепи, обладающей заданными характерными свойствами (частотными, временными). Исходным материалом для синтеза является характеристика цепи. В итоге надо получить схему цепи и величины элементов. При рассмотрении характеристик следует обратить внимание на условие физической реализуемости, т.е. получения реальных элементов для цепи (чтобы не было отрицательных или мнимых величин элементов и т.д.). Эти условия сильно зависят от выбранного типа ЭЦ (пассивная цепь, активная и т.д.). Есть ограничения на характеристики (теоретические и практические ограничения).

Синтез реактивного ДП является частным случаем синтеза цепи в классе пассивных ДП с LC- элементами. В простейшем случае для синтеза реактивного ДП задаются резонансные частоты и уровень величины сопротивления на какой – то частоте. По величине сопротивления определяется множитель Н. Сам синтез ведется по каноническим схемам (стандартно по четырем), потом выбирается какая – то одна схема по дополнительным критериям. Дополнительным критерием может быть, например, меньшее количество индуктивности или меньшая величина суммарной индуктивности. Для каждой канонической схемы используется своя математическая процедура.

Синтез по первой схеме Фостера

Здесь математическая процедура основана на разложении функции сопротивления по полюсам этой функции. Полюсы в начале и конце координат дают по одному элементу, а на конкретной частоте дают сразу пару элементов или параллельный контур.

где

Для удобства вычислений, Z(p) надо представить в виде выражения из теоремы Фостера из произведения скобок в операторном виде (особенно для знаменателя).

Синтез по второй схеме Фостера

Во второй схеме Фостера синтез ведется с использованием разложения функции проводимости по ее полюсам, все остальное аналогично. В схеме будет столько последовательных контуров сколько частот резонансов напряжений (скобок знаменателя проводимости)

Синтез по первой схеме Кауэра

Функцию сопротивления записывают в виде отношения полиномов по уменьшающимся степеням (Н вносят в числитель)

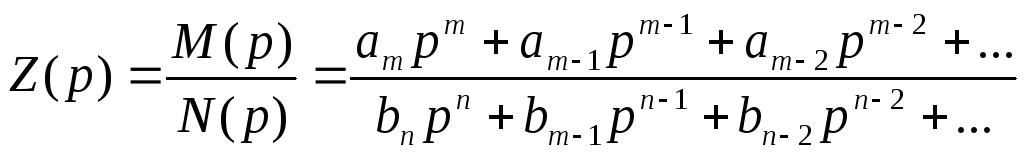
Далее делают разложение в цепную дробь путем деления числителя на знаменатель с выделением оператора и остатка :

Деление возможно произвести только когда старшая степень числителя m>n (старшая степень знаменателя). После деления в слагаемом степень числителя меньше степени знаменателя. Осуществляется ее переворот:

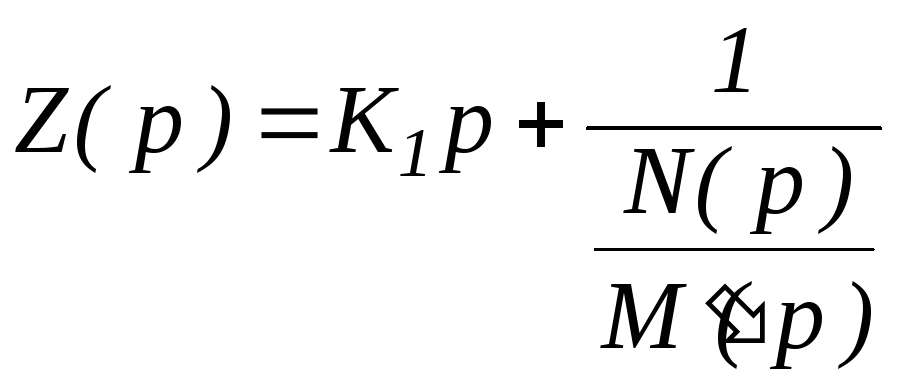Теперь раскладывается дробь :

Далее действия проводятся аналогично до полного разложения.

Коэффициенты К₁, К₂, К₃, ... ставятся в соответствии со схемой, т.е. в первой схеме Кауэра К₁= L_1. а К₂ =С₂. Если первоначально m<n, то сразу делается переворот дроби и эта первая индуктивность отсутствует (для классов 0-0 и 0-∞).

Синтез по второй схеме Кауэра

Производится аналогично разложением функции сопротивления в цепную дробь, но при выделении слагаемых с р^-1. Для такого разложения сопротивление записывают с помощью полиномов. Полиномы располагают в порядке увеличения степеней.

Далее производят деление сопротивления ДП с выделением остатка и последующим переворотом :

Такое деление возможно если числитель четный, а знаменатель нечетный. Если наоборот, то первое деление пропускают и переходят сразу к перевороту дроби и делают деление..

Количество элементов в любых канонических схемах одинаково и соответствует самой старшей степени полинома.