3.8.5. Фильтры со всплесками ослабления (на основе дробей Чебышева и Золотарева)

Частотные характеристики полиномиальных фильтров имеют монотонный характер в полосе непропускания. В частности, рабочее ослабление таких фильтров монотонно возрастает по мере удаления от полосы пропускания.

При «жестких» требованиях к частотным характеристикам (малая переходная область между полосами пропускания и непропускания и большая величина рабочего ослабления в полосе непропускания) порядок фильтра m может получиться большим даже в случае применения полинома Чебышева. Это приведет к существенному усложнению фильтра и к большому количеству элементов. В таких случаях целесообразно применять фильтры со всплесками рабочего ослабления в полосе непропускания. На частотах всплеска и т.д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области (аналогично применению звеньев m).

Среди фильтров со всплесками ослабления наиболее широкое распространение получили фильтры Чебышева и Золотарева (Кауэра). Чтобы получить частотные характеристики фильтра на основе дробей Чебышева, нужно в качестве функции фильтрации использовать дробь Чебышева. Обозначая ее , получим:

(8)

В качестве примера укажем дробь Чебышева пятого порядка, для которой и был построен предыдущий график:

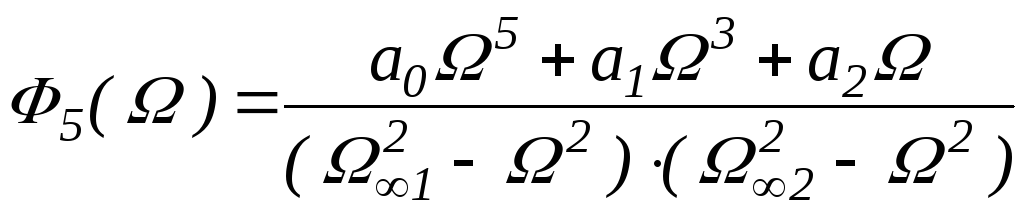
В полосе пропускания дробь Чебышева ведет себя так же, как и полином Чебышева, т.е. рабочее ослабление фильтра носит равно волновой характер. На частотах всплеска дробь Чебышева обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.

Следует отметить, что дробь Чебышева является дробью наилучшего приближения.

Частным случаем дробей Чебышева являются дроби Золотарева:

, где

, , значение S равно 0 для четных m и равно 1 для нечетных m; m – порядок дроби; - нули и полюсы дроби, связанные соотношением: .

Используя в качестве функции фильтрации дроби Золотарева, получим:

Понятно, что нули функции совпадают с нулями дроби Золотарева, а всплески функции - с полюсами той же дроби.

Дроби Золотарева так же, как и Чебышева, дают равно волновую характеристику рабочего ослабления фильтра в полосе пропускания. Однако в полосе непропускания у фильтров Золотарева значения всех минимумов рабочего ослабления оказываются одинаковыми и равными значению рабочего ослабления на частоте . Такие фильтры называются также фильтрами с изоэкстремальными характеристиками рабочего ослабления.

Фильтры с характеристиками Золотарева можно рассматривать как частный случай фильтров с характеристиками Чебышева, когда значения минимумов ослабления фильтра в полосе непропускания выровнены, а число всплесков – минимально возможное при выбранном значении m.

3.9. Методики реализации схем фильтров

3.9.1. Лестничные полиномиальные lc-фильтры

Любые рассмотренные выше фильтры могут быть реализованы в виде LC-цепей.

Пассивные LC-фильтры обычно представляют собой реактивный лестничный ЧП, включенный между генератором с активным внутренним сопротивлением R_г и нагрузкой с активным сопротивлением R_н.

2

U₁ U₂

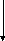
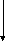
Если фильтр со стороны зажимов 1 - 1^′ рассматривать как ДП, образованный реактивным ЧП и нагрузкой R_Н, то, зная выражение Z_ВХ1(р), можно реализовать данный ДП одним из известных в теории цепей методом синтеза ДП. Таким образом, задача реализации фильтра сводится к реализации ДП по его заданному входному сопротивлению. Идея данного подхода принадлежит С. Дарлингтону и метод реализации фильтров называется методом Дарлингтона.

На входе фильтра имеет место несогласованность, которую можно оценить, введя в рассмотрение коэффициент отражения:

Используя нормирование по сопротивлению получают формулу нормированного входного сопротивления

Коэффициент отражения ρ(р) связан с передаточной функцией Н_р(р)=ω(р)/υ(р) и функцией фильтрации соотношением:

Откуда следует, что знаменатель у ρ(р) такой же, как и у Н_р(р): им является полином υ(р). Остается найти нули правой части выражения знаменателя и половину из них, которые находятся в левой полуплоскости, «приписать» полиному знаменателя v(р). Полином формируется из нулей по теореме Виета.

1+ε²В ²_n (р) =0, v(p)=(p-p₁)(p-p₂(p-p₃)….(р-р_n).

Нетрудно показать, что определяется при аппроксимации по Баттерворту

и по Чебышеву Здесь учитывается не равенство 1 коэффициента при старшей степени.

Для аппроксимации по Баттерворту: pⁿ – нормированный полином Баттерворта Затем осуществляется разложение в нормированную дробь по Кауэру, причем в конце разложения получается вещественное число, соответствующее сопротивлению нагрузки равное 1. Нормированное сопротивление источника то же равно1.

(верхние знаки) (нижние знаки)

Коэффициенты разложения дают нормированные величины элементов и получается схема разная при верхних и нижних знаках. Выбирают обычно ту, где меньше индуктивностей.

Для Чебышева:

- полином Чебышева от р. Получается заменой Ω=р и при этом все знаки коэффициентов берутся положительными.

Схемы такие же. Когда n – нечетное, . Когда n – четное, то у фильтра Чебышева .

При при n четном; при n нечетном.

Затем делается денормирование – переход к реальным величинам элементов:

R_H(2)=R_Г(1)▪r_n(H)

Первичная проверка ведется в схеме без потерь в основном, по полиномам. Затем проверка проводится по схеме, а далее с учетом и потерь элементов. Эта проверка может иметь форму расчетов или экспериментального моделирования.

Синтез электрического фильтра производится в следующем порядке:

1. Переход к ФНЧП и нормирование частот;

2. Аппроксимация рабочей передаточной функции и характеристики рабочего ослабления;

3. Реализация схемы ФНЧ (ФНЧП);

4. Переход от схемы ФНЧП к схеме заданного фильтра и денормирование ее элементов;

5. Расчет и построение денормированных частотных характеристик рабочего ослабления и фазы.