БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ИНЖЕНЕРНО – СТРОИТЕЛЬНЫЙ ФАКУЛЬТЕТ

КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ

Лабораторная работа № 3

по дисциплине

Локальные системы управления

Исследование системы прямого цифрового управления с датчиком

типа ЛИР-20

Выполнила ст. гр. УИТ – 52

Горев Р. Н.

Проверил преподаватель

Комлева О. А.

2008

Данная работа подразделяется на два этапа.

Данные для расчета:

i = 16 k= 0,03;

k= 6,28; = 16;

n = 36; = 24;

k= 0,069; g= 2;

k= 2,75; =6;

= 2,033; Т_ШИМ= 2,75;

Т= 0,75; Т= 1,33;

= 12,5; t= 12,4.

T_p= 1,88;

I ЭТАП

Целью первого этапа работы являются:

1. Изучение принципа действия и условий формирования выходных сигналов унитарно-кодового датчика ЛИР-20.

2. Знакомство с устройствами формирования ШИМ в системе прямого цифрового управления.

3. Определить характеристик исполнительного двигателя в режиме ШИМ.

Исследуемая система прямого цифрового управления включает в себя ПЭВМ со встроенной платой цифрового ввода/вывода ЛА-ТМР, усилитель-преобразователь, исполнительный двигатель, инкрементный датчик угла ЛИР-20, схему формирования сигнала направления вращения двигателя.

ПЭВМ совместима с IBM PC и содержит плату ЛА-ТМР. Плата является частью устройства связи с объектом и выполняет определенные задачи, присущие технологическим контроллерам. Через нее осуществляется обмен информации между ОУ и ЭВМ, и формирует ШИМ-сигнал. Она содержит:

– 6 шестнадцатиразрядных счетчиков-таймеров Intel P82C54;

– высокостабильный кварцевый генератор с частотой 10 МГц;

– 16 цифровых линий, организованных как 8 входов и 8 выходов;

– линии стробирования;

– 2 независимые линии запроса прерывания для IBM PC.

На счетчик-таймер могут быть поданы сигналы с частотой 10 или 1 МГц.

УП является усилителем мощности с гальванической развязкой и обеспечивает преобразованием 2 сигналов в сигнал, пропорциональный напряжению и позволяющий осуществлять измерение направления вращения двигателя.

В качестве исполнительного двигателя используется двигатель Д-25Г.

Обратная связь осуществляется с помощью инкрементного датчика угла ЛИР-20, в основе которого лежит принцип фотоэлектрического сканирования штриховых растворов. На рисунке представлены временные диаграммы выходных сигналов датчика. Этот датчик обеспечивает сдвиг фаз между выходными сигналами А и В на четверть шага.

Датчик связан с двигателем через редуктор с передаточным числом i=16.

Структурная схема разомкнутой системы.

Учитывая, что период дискретизации на несколько порядков меньше длительности переходных процессов в системе и шаг дискретизации достаточно мал (1/1000 оборота или 0,006 рад), можно рассматривать систему управления как непрерывную.

Пологая, что постоянные времени усилителя-преобразователя (Т_УП=с) и якорная постоянная двигателя Т_Яс, примем передаточные функции элементов в следующем виде: ; ; ;

.

Для измерения скорости используется схема, представленная на рисунке. Штриховой линией выделены блоки, реализованные программно.

Т. о. положение и скорость можно вычислить:

;

где = 6,

n – количество полученных от датчиков импульсов (36 импульсов).

Воздействие задается как отношение Т_Р/Т_ШИМ=1.88/2.75=0.684, где Т_Р- время, в течение которого на выходе ШИМ формирователя установлена единица (рабочий период); Т_ШИМ- период ШИМ.

Отрицательное значение обозначало бы, что вращение идет в обратную сторону.

Значение частоты ШИМ влияет на тепловые потери в якоре двигателя, которые определяются эффективным значением тока якоря. Поэтому при выборе частоты ШИМ для снижения эффективного значения тока необходимо исходить из требуемого соотношения между электрической постоянной времени двигателя и частотой ШИМ, которое должно подчиняться неравенству:

f , f, f.

С учетом приведенных ПФ элементов структурной схемы ПФ разомкнутой системы имеет вид:

,

где К= - коэффициент передачи разомкнутой системы.

По регулировочной характеристике , где g задается в условных единицах (Т/T), можно рассчитать k как отношения приращения скорости к приращению входного воздействия g:

k=k·k, k= 0,069·2,75 = 0,19.

Тогда К = k· k· k= 0,19·6,28·0,0625 = 0,0746.

Сняв разгонную характеристику двигателя , учитывая принятую модель его математического представления, можно уточнить Т_ЭМ при выбранном значение ШИМ, в соответствии с тем, что

где - начальная скорость, - изменение скорости за весь период переходного процесса. При t = T_ЭМ:

.

Переходный процесс:

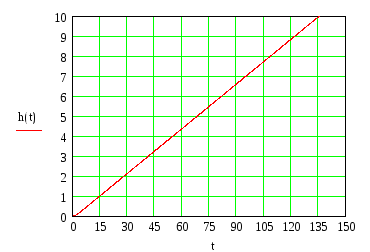
Вывод: Значение частоты ШИМ влияет на тепловые потери в якоре двигателя, которые определяются эффективным значением тока якоря. Сняв разгонную характеристику двигателя , учитывая принятую модель его математического представления, можно уточнить Т_ЭМ при выбранном значение ШИМ. Найдя на графике переходного процесса и соответствующее ему значение времени t = 132с, можно определить электрическую постоянную времени двигателя T_ЭМ.

II этап

Целью второго этапа работы является:

1. Изучение возможных вариантов построения систем прямого цифрового управления с датчиком перемещения ЛИР-20, сравнение вариантов.

2. Расчет регуляторов системы прямого цифрового управления для разных вариантов структурной организации (одно- и двухконтурной систем).

3. Исследование статических и динамических характеристик системы прямого цифрового управления как позиционной системы при отработке малых, средних и больших перемещений.

4. Исследование характеристик системы при типовых воздействиях g(t)=g₀t и g(t)=(g₀/2) t².

При решение задач синтеза и анализа системы будем рассматривать ее как линейную. Структурная схема одноконтурной системы регулирования положения:

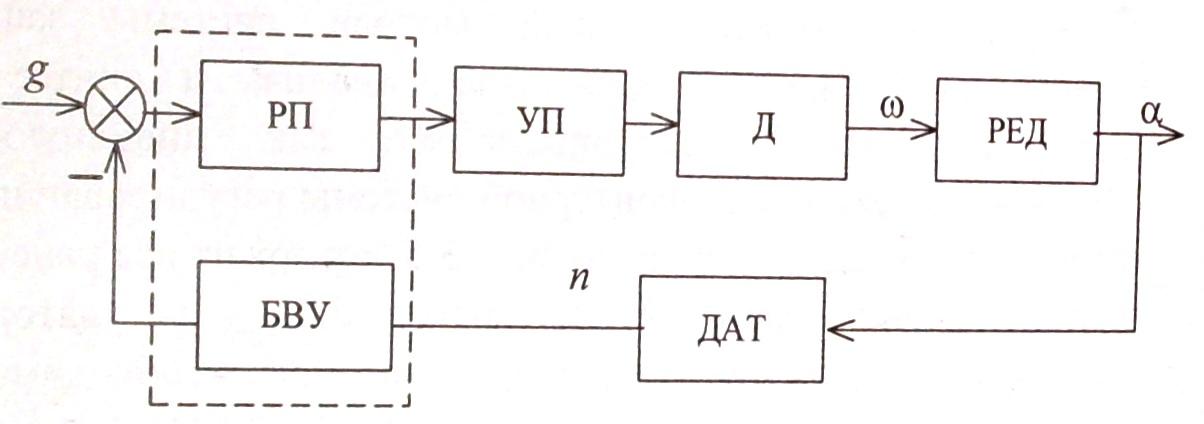
Содержит все ранее перечисленные элементы, а так же РП - регулятор положения, БВУ – блок вычисления угла W_БВУ(s)=1/k_ДАТ.

W(s) = W(s) = 0,159.

Передаточная функция двигателя имеет вид:

Существенное влияние на значение некомпенсируемой постоянной времени Т_и оказывает дискретность датчика, а также задержки в ПЭВМ. Задержки, возникающие из-за дискретности датчика, зависит от скорости вращения вала двигателя, при малых скоростях она возрастает. Учитывая это, в первом приближении можно принимать значение некомпенсируемой постоянной времени контура положения .

Синтез замкнутой системы можно провести исходя из требований минимального времени регулирования, что соответствует настройке контура на модульный оптимум. В этом случае необходимо обеспечить ПФ разомкнутой системы контура в виде:

.

ПФ разомкнутого контура в соответствии с рисунком:

,

откуда

Подставив ПФ всех звеньев, получим ПФ регулятора:

.

Получили ПД-регулятор, который физически нереализуем, так как степень полинома числителя выше степени полинома знаменателя. Проанализируем возможность замены ПД-регулятора на П-регулятор, т.е. Запишем ПФ разомкнутой системы для этого случая:

.

Для упрощения дальнейших расчетов пренебрежем членом и представим ПФ разомкнутой системы в виде:

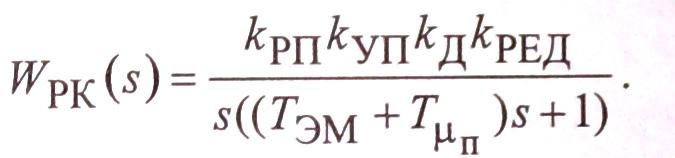
Для анализа полученного результата запишем ПФ замкнутого контура:

ПФ представляется в виде колебательного звена:

Подставим значения:

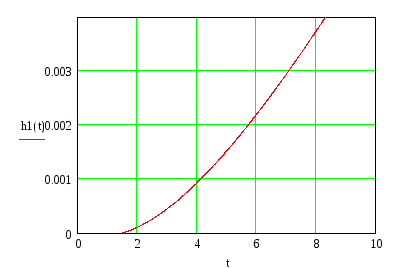
При переходный процесс в системе является апериодическим, а при перерегулирование в системе составляет 4,3%, а время переходного процесса минимально. Можно найти коэффициент регулятора положения:

.

Для системы регулирования положения в общем случае требуется построение трехконтурной системы (тока, скорости и положения). При посторенние маломощных систем можно отказаться от контура тока, перейдя к двухконтурной системе. В нее добавили БВС – блок вычисления скорости, датчик скорости, датчик положения.

Не компенсируемая постоянная времени в контуре скорости можно оценить как .

Контур скорости

ПФ разомкнутого контура скорости:

Вычисляет скорость, приведенную к валу двигателя

Исходя из оптимум, ПФ разомкнутого контура скорости должна быть:

.

Тогда получает ПФ регулятора скорости:

.

Контур положения

ПФ замкнутого контура скорости:

.

Некомпенсируемая постоянная времени контура положения равна . ПФ разомкнутого контура положения и при настройке на модульный оптимум откуда ПФ регулятора положения:

.

В результате получен П-регулятор положения с коэффициентом передач:

.

В данном случае имеем линейную зависимость входного параметра регулятора от рассогласования () на его входе. Такой регулятор обеспечивает хороший переходный процесс при отработке малых и средних перемещений, когда скорость двигателя не достигает мах значения. При отработке больших рассогласований требуется нелинейный регулятор. Необходим регулятор со статической характеристикой При этом .

Расчет нелинейного регулятора положения в общем случае для непрерывной системы регулирования приводит к следующему результату:

7.756.

= 10 – максимальная скорость двигателя.