5. Математическая статистика
● Основные характеристики выборочной и генеральной совокупностей. Точечные оценки
-
Игральную кость бросили
 раз. При этом
раз. При этом
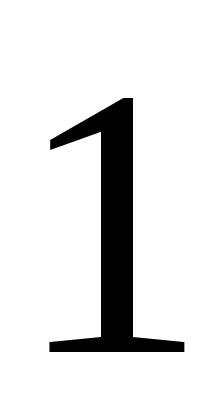 очко выпало
очко выпало
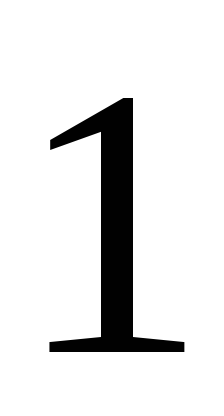 раз,
раз,
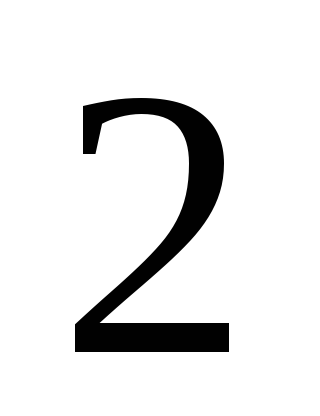 очка –
очка –
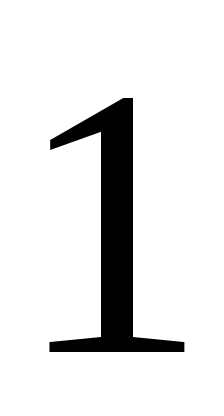 раз,
раз,
 очка –
очка –
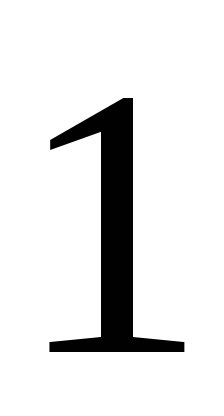 раз,
раз,
 очка –
очка –
 раза,
раза,
 очков –
очков –
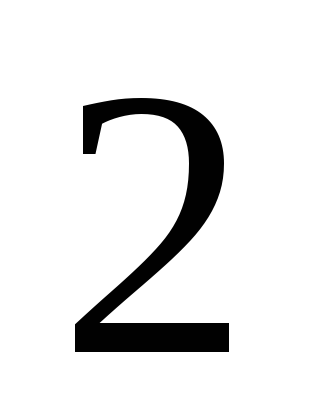 раза,
раза,
 очков –
очков –
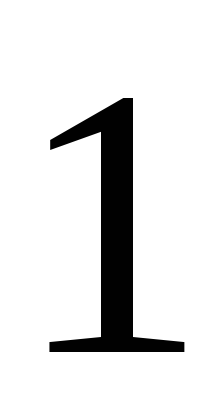 раз. Найдите эмпирическую функцию
распределения числа очков, выпавших
при бросании игральной кости.
раз. Найдите эмпирическую функцию
распределения числа очков, выпавших
при бросании игральной кости.
|
Xi |
1 |
2 |
3 |
4 |
5 |
6 |
|
Ni |
1 |
1 |
1 |
2 |
2 |
1 |
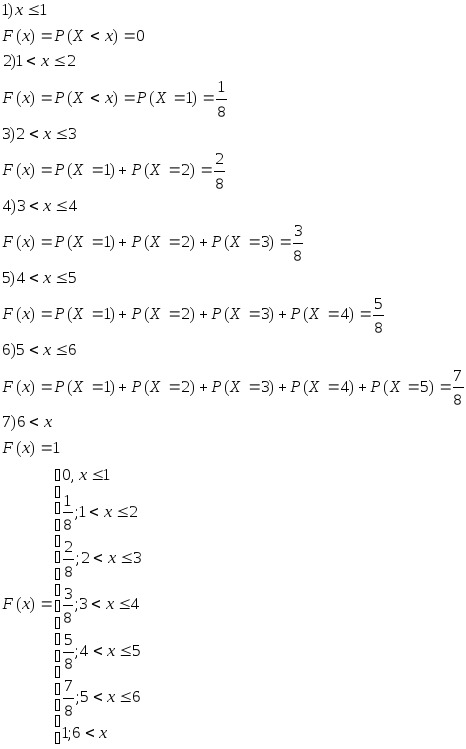
-
В четырех независимых испытаниях случайная величина
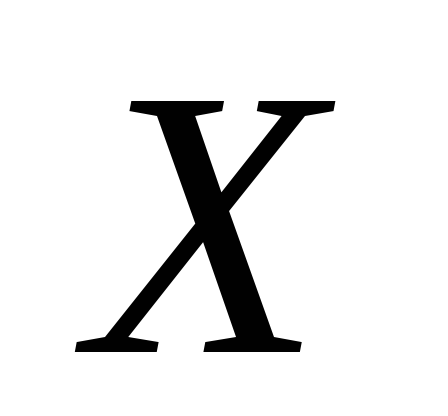 приняла следующие значения:
приняла следующие значения:



 Найдите несмещенную оценку дисперсии
Найдите несмещенную оценку дисперсии
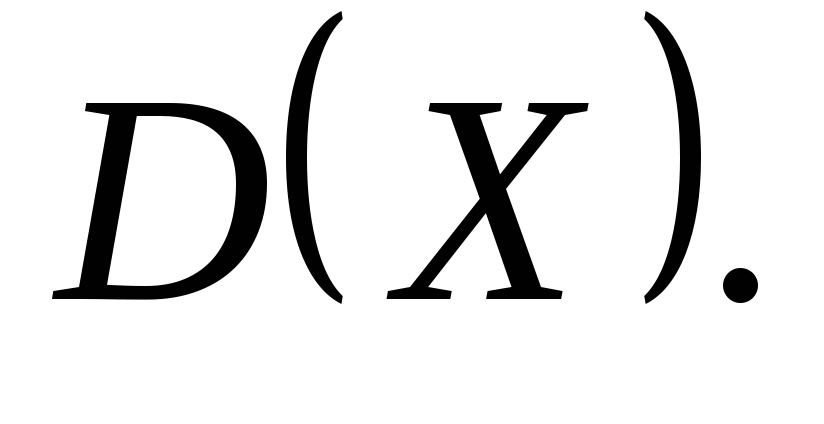
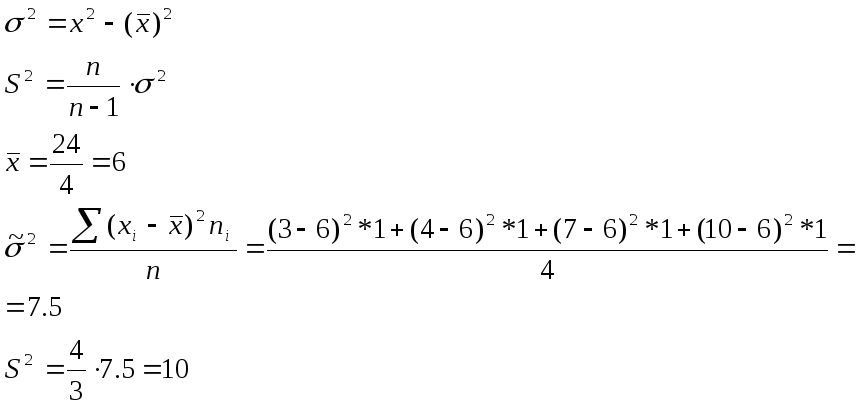
-
В
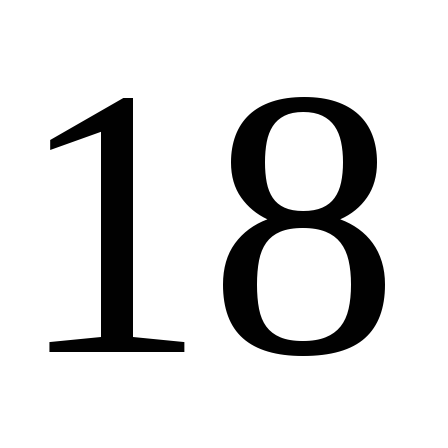 независимых испытаниях случайная
величина
независимых испытаниях случайная
величина
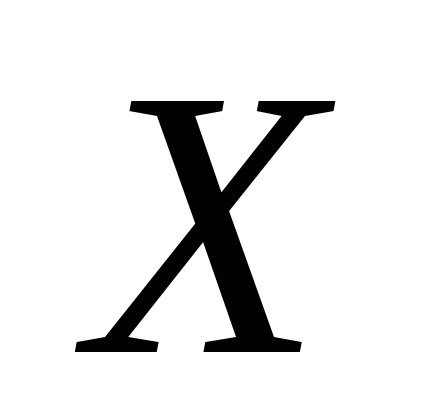 значениe
значениe
 приняла
приняла
 раз, а значение
раз, а значение
 –
–
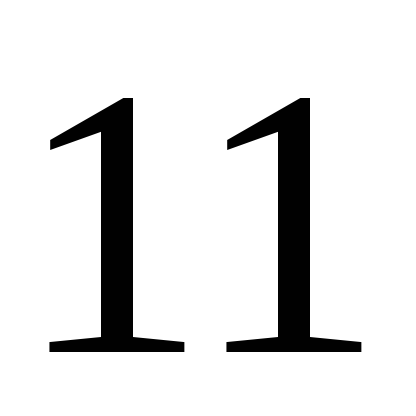 раз. Найдите несмещенную оценку дисперсии
раз. Найдите несмещенную оценку дисперсии
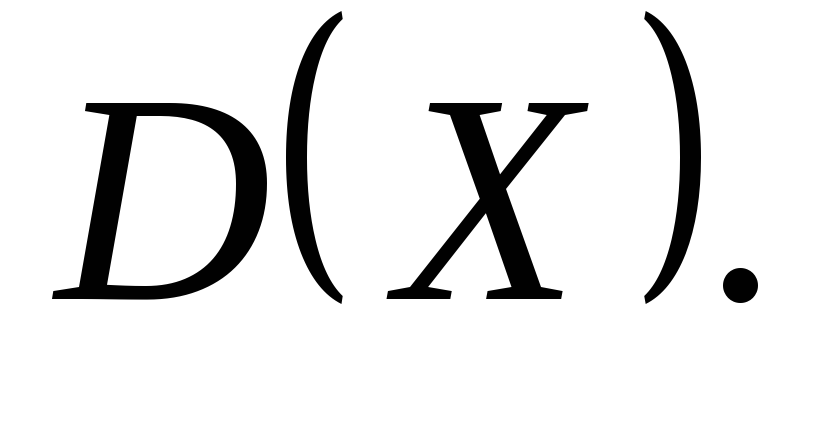
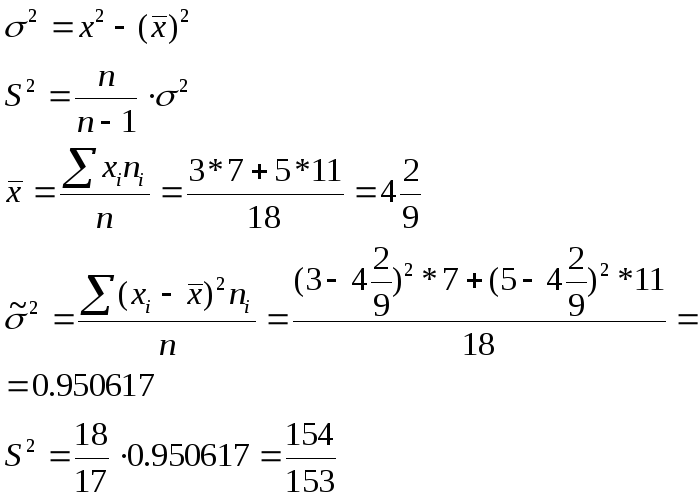
-
Даны результаты
 независимых измерений одной и той же
величины прибором, не имеющим
систематических ошибок:
независимых измерений одной и той же
величины прибором, не имеющим
систематических ошибок:
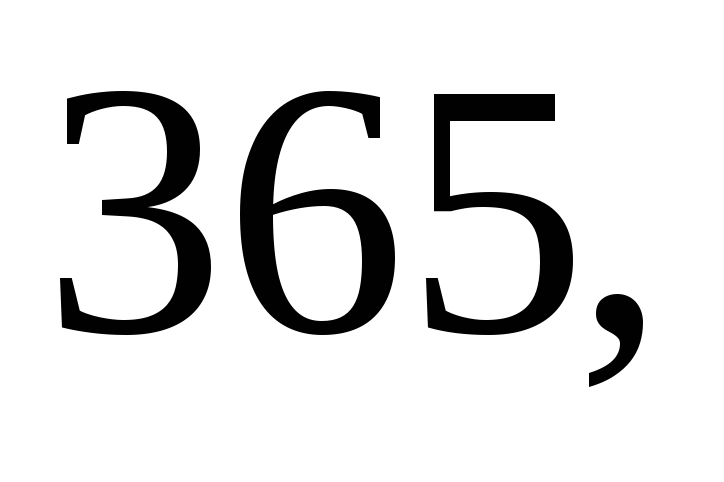

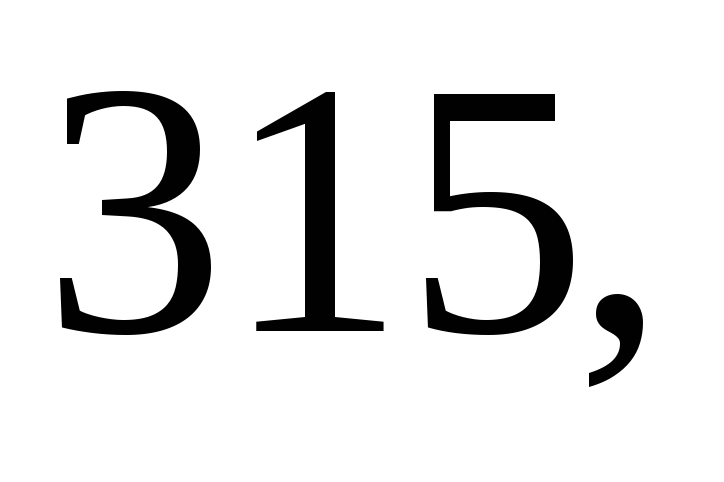
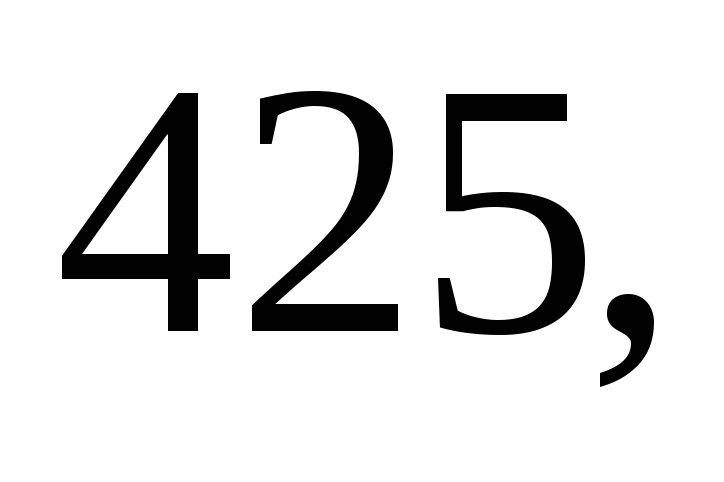
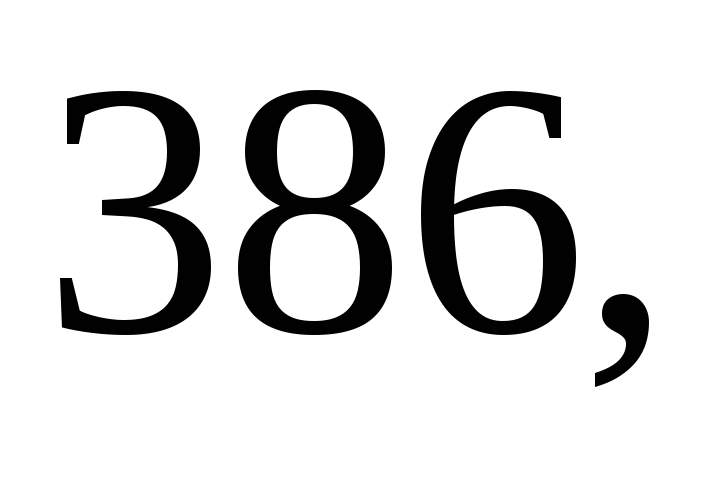
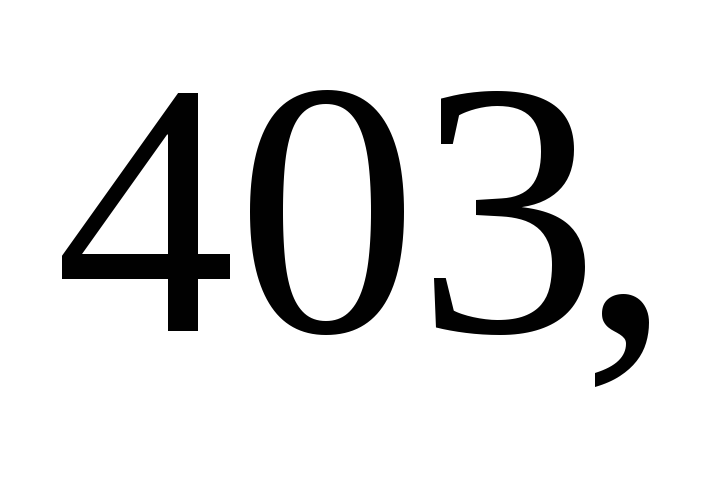

 м. Найдите несмещённую оценку дисперсии
ошибок измерений, если истинная длина
м. Найдите несмещённую оценку дисперсии
ошибок измерений, если истинная длина
 м.
м.
-
Даны результаты
 независимых измерений одной и той же
величины прибором, не имеющим
систематических ошибок:
независимых измерений одной и той же
величины прибором, не имеющим
систематических ошибок:
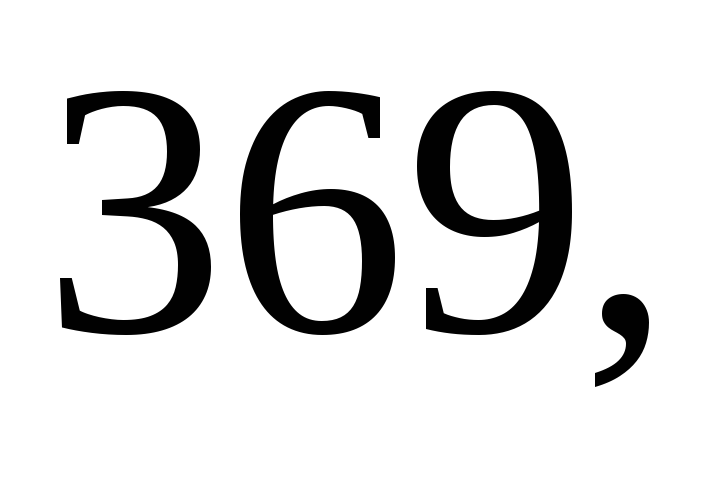
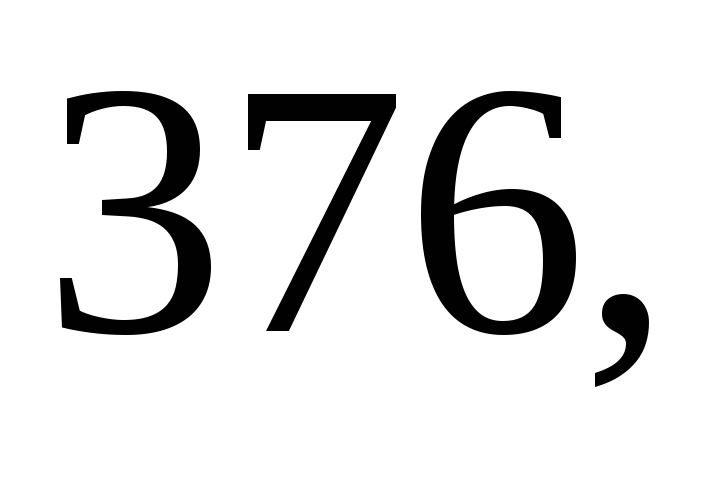
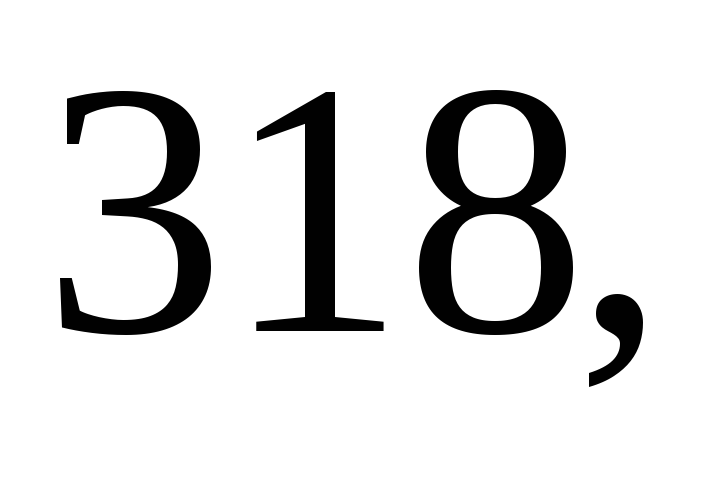
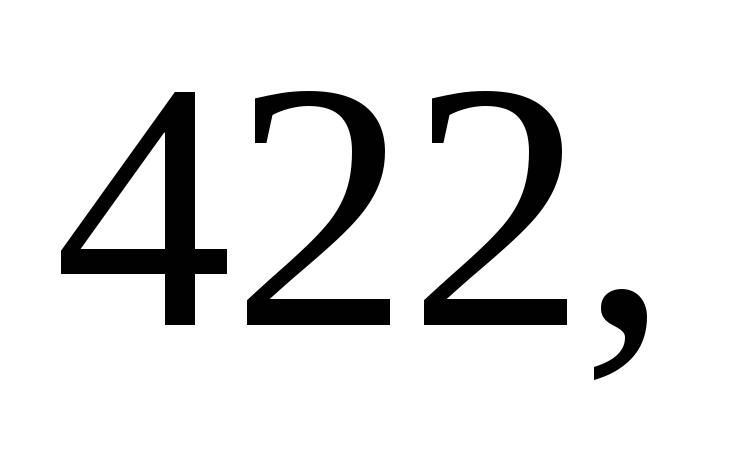
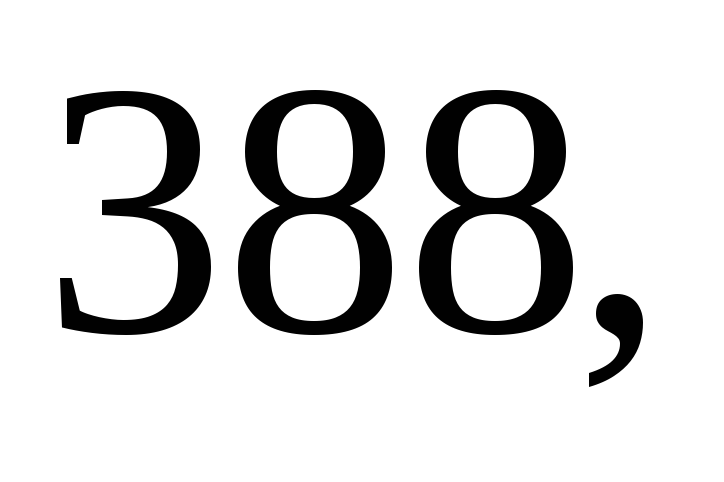
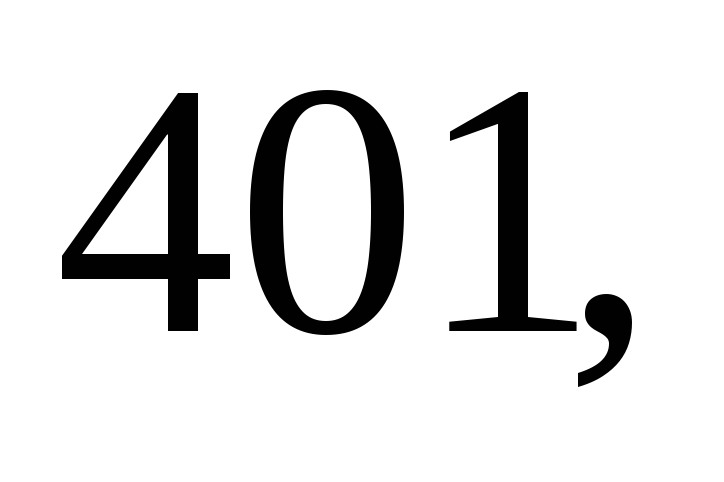
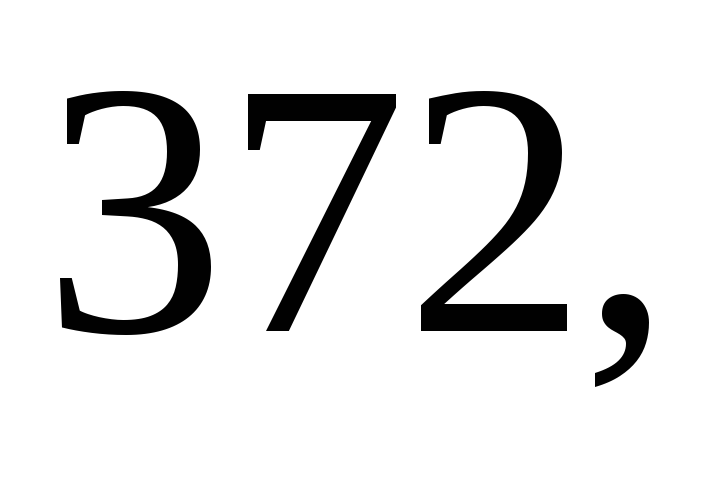
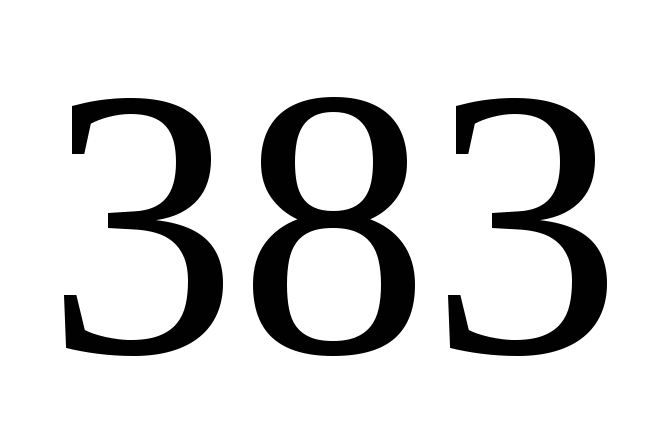 м. Найдите несмещённую оценку дисперсии
ошибок измерений, если истинная длина
неизвестна.
м. Найдите несмещённую оценку дисперсии
ошибок измерений, если истинная длина
неизвестна.
-
Используя метод моментов, оцените параметры
 и
и
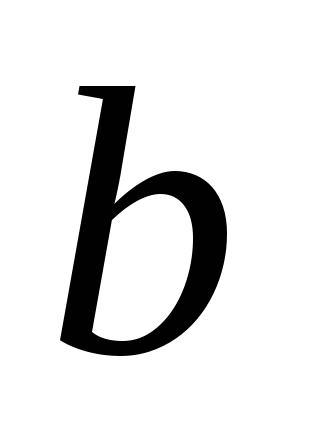 равномерного распределения на отрезке
равномерного распределения на отрезке
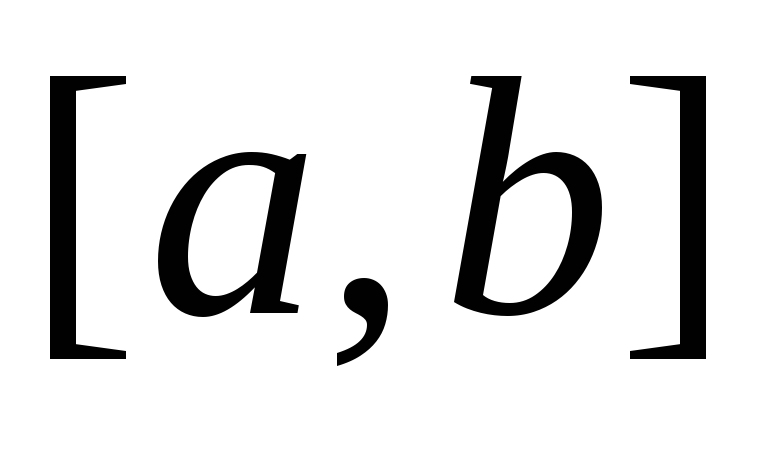 по эмпирическому распределению
по эмпирическому распределению
-
Значение

3
5
7
9
Частота
21
18
15
26
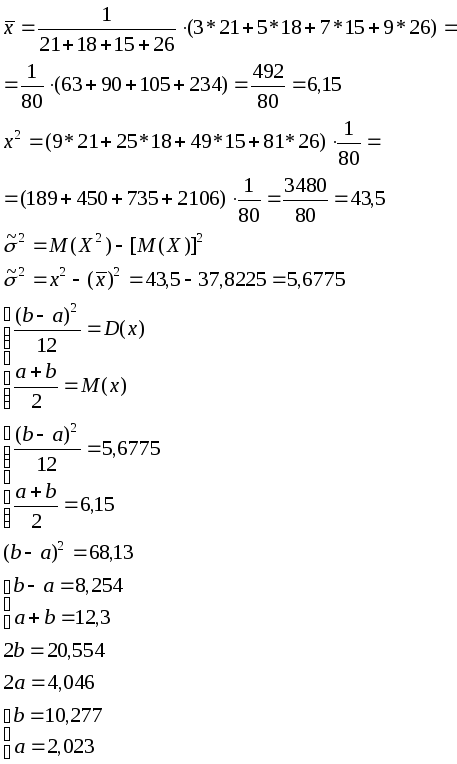
-
Случайная величина
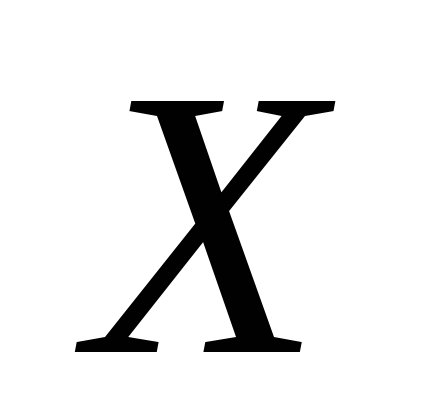 (время бесперебойной работы устройства)
имеет показательное распределение с
плотностью
(время бесперебойной работы устройства)
имеет показательное распределение с
плотностью
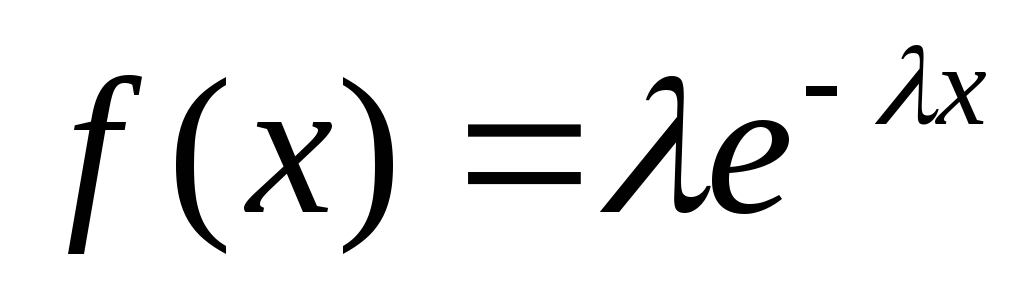 (
(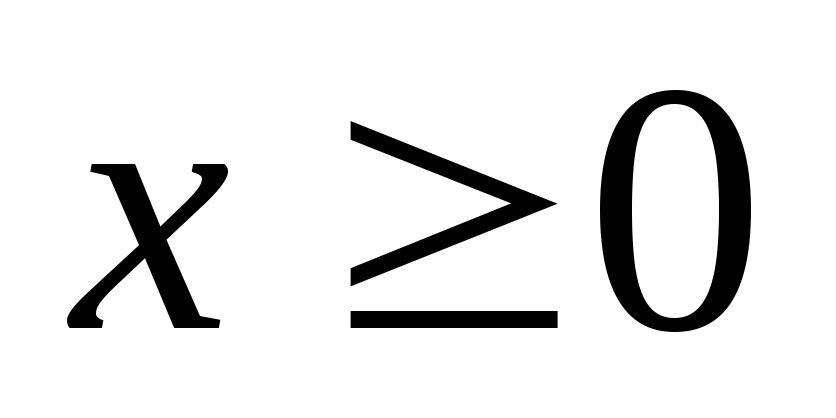 ).
По эмпирическому распределению времени
работы
).
По эмпирическому распределению времени
работы
|
Время работы |
|
|
|
|
|
Число устройств |
|
|
|
|
методом моментов
найдите точечную оценку
![]() .
.
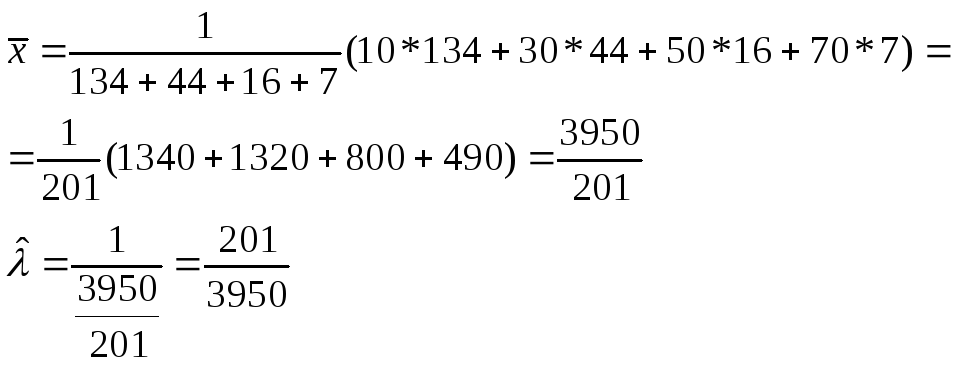
-
Случайная величина
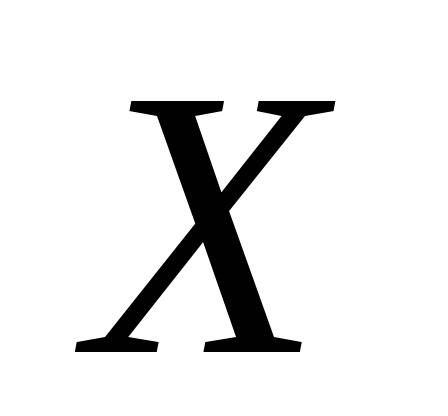 распределена по закону Пуассона
распределена по закону Пуассона
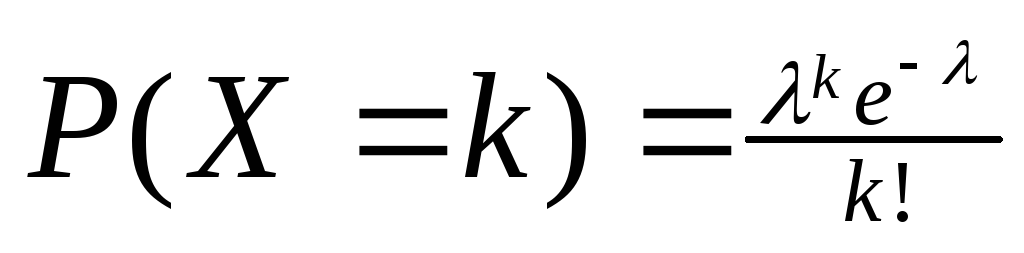 .
Результаты
.
Результаты
 независимых наблюдений
независимых наблюдений
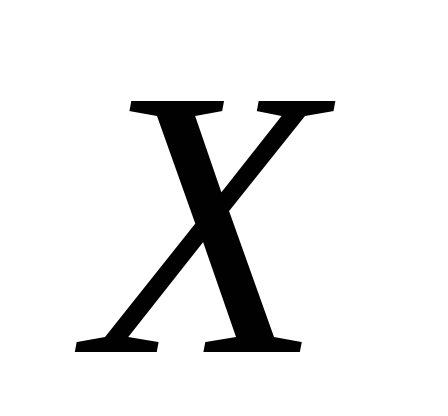 отражены в таблице
отражены в таблице
|
Значение
|
0 |
1 |
2 |
3 |
|
Частота |
|
|
|
|
Найдите методом
моментов точечную оценку
![]() .
.

● Интервальные оценки параметров распределения
-
В
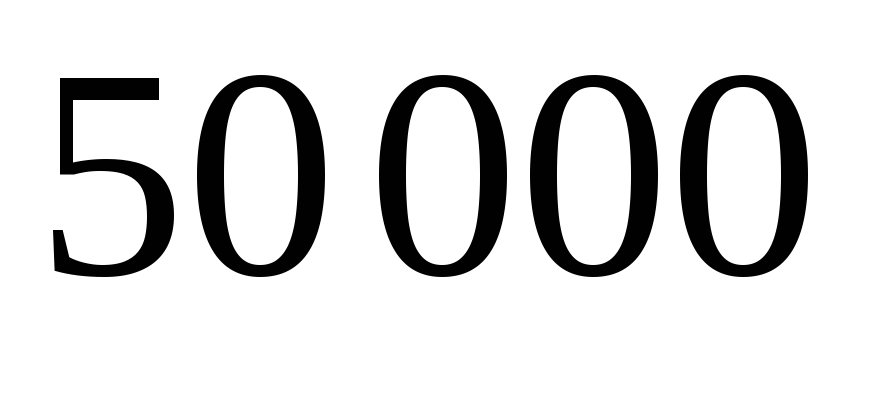 сеансах игры с автоматом выигрыш
появился
сеансах игры с автоматом выигрыш
появился
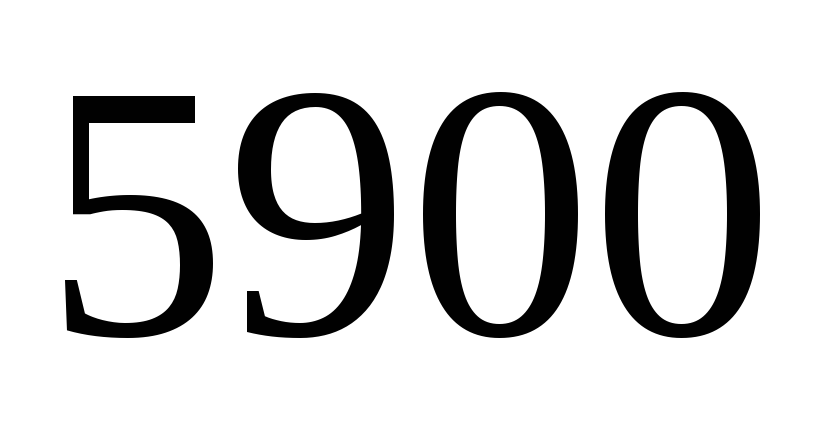 раз. Найдите для вероятности выигрыша
раз. Найдите для вероятности выигрыша
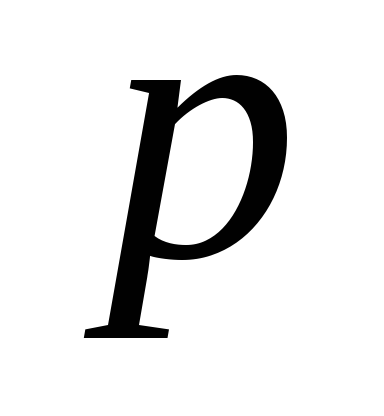 приближенный
приближенный
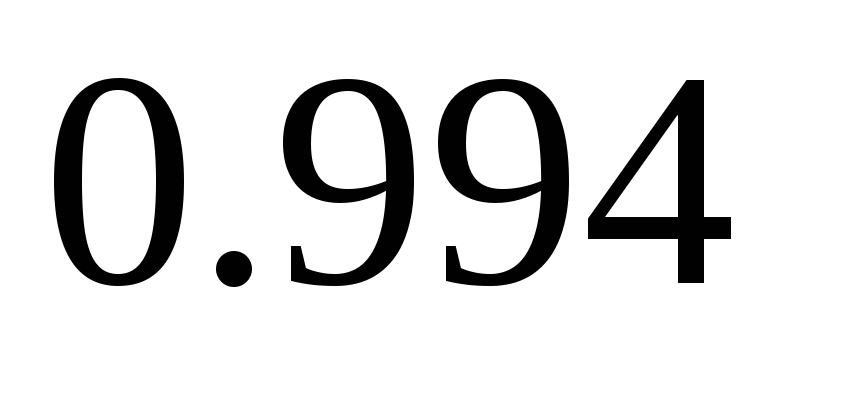 – доверительный интервал.
– доверительный интервал.

-
Глубина моря измеряется прибором, систематическая ошибка которого равна
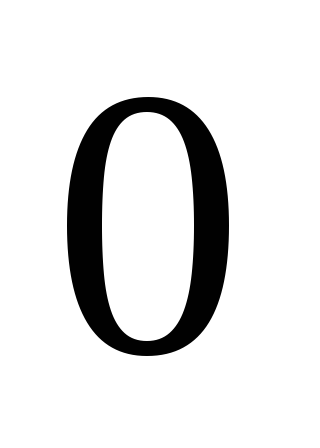 ,
а случайные ошибки распределены
нормально со среднеквадратичным
отклонением
,
а случайные ошибки распределены
нормально со среднеквадратичным
отклонением
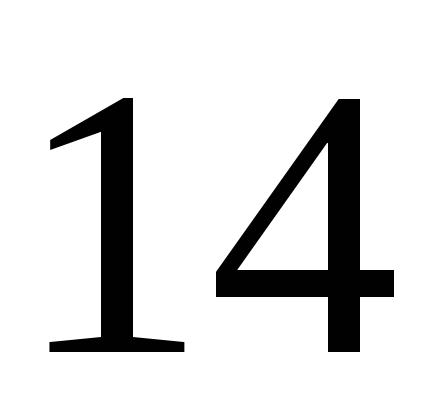 м. Каково наименьшее число независимых
измерений, при котором удается определить
глубину с ошибкой меньше
м. Каково наименьшее число независимых
измерений, при котором удается определить
глубину с ошибкой меньше
 метров с надежностью не ниже
метров с надежностью не ниже
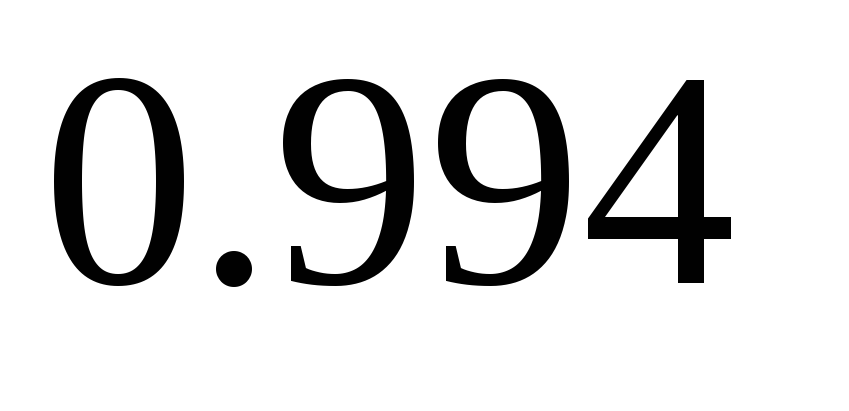 ?
?
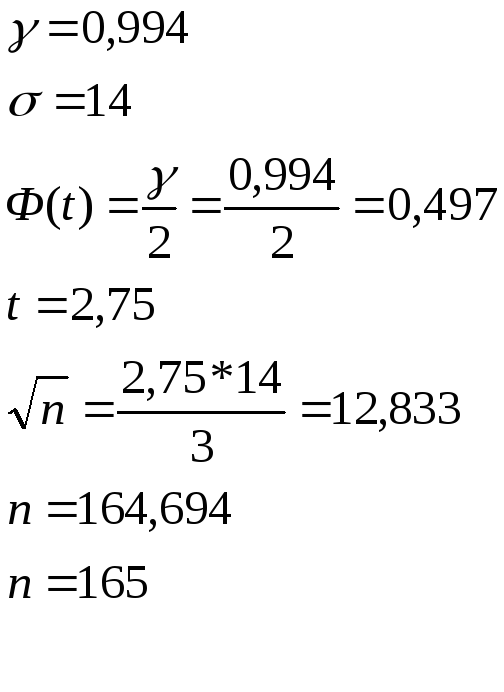
-
Брокер на бирже желает найти
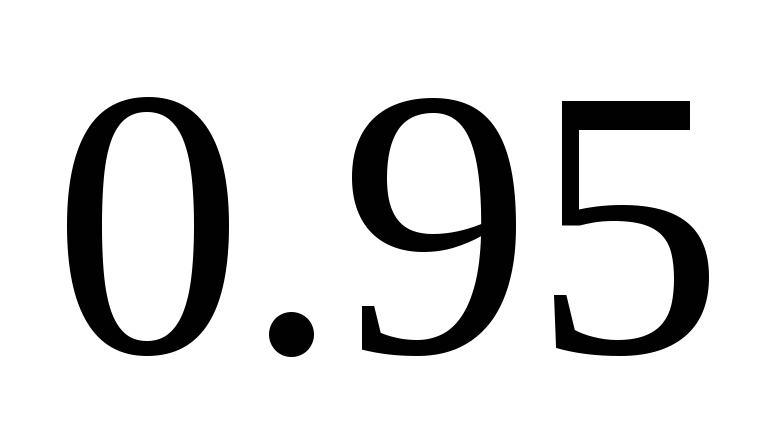 -доверительный
интервал для математического ожидания
недельной доходности выбранной акции.
Известно, что выборочная средняя
недельная доходность за последний год
(52 недели) составила
-доверительный
интервал для математического ожидания
недельной доходности выбранной акции.
Известно, что выборочная средняя
недельная доходность за последний год
(52 недели) составила
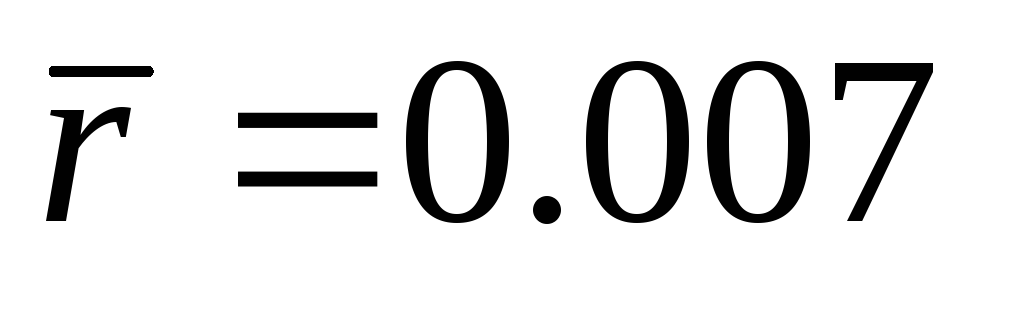 .
Найдите искомый доверительный интервал
в предположении, что недельные доходности
независимы и распределены нормально
с постоянными параметрами, причем
генеральное среднеквадратичное
отклонение недельной доходности равно
.
Найдите искомый доверительный интервал
в предположении, что недельные доходности
независимы и распределены нормально
с постоянными параметрами, причем
генеральное среднеквадратичное
отклонение недельной доходности равно
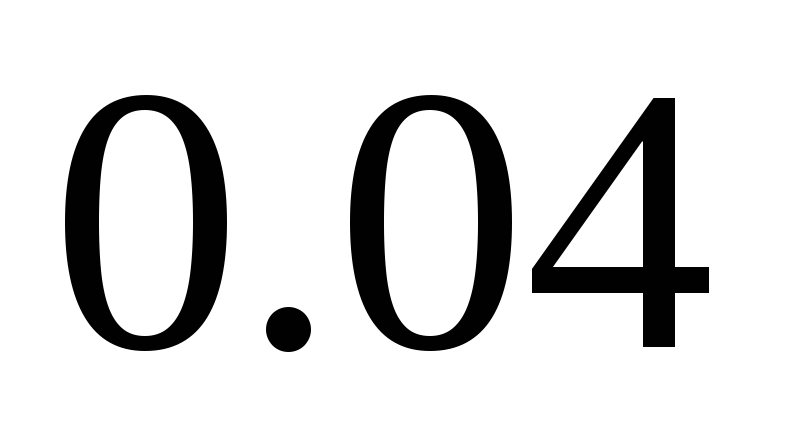 .
.
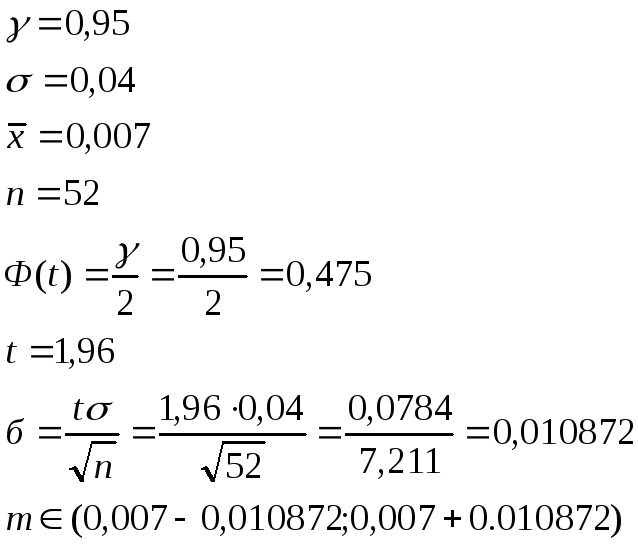
-
Найдите
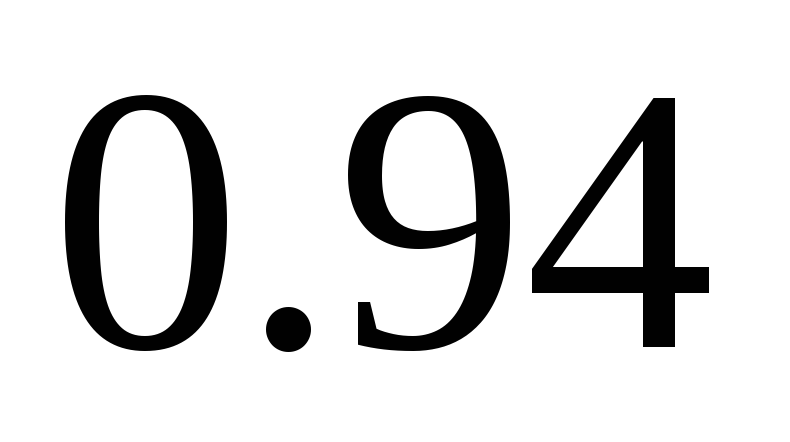 ‑доверительный
интервал для генерального среднего
нормально распределенного признака
‑доверительный
интервал для генерального среднего
нормально распределенного признака
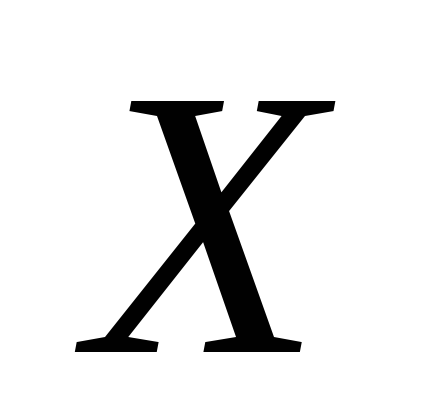 ,
если генеральное среднеквадратичное
отклонение равно
,
если генеральное среднеквадратичное
отклонение равно
 ,
а выборочное среднее при объеме выборки
,
а выборочное среднее при объеме выборки
 равно
равно
 .
.
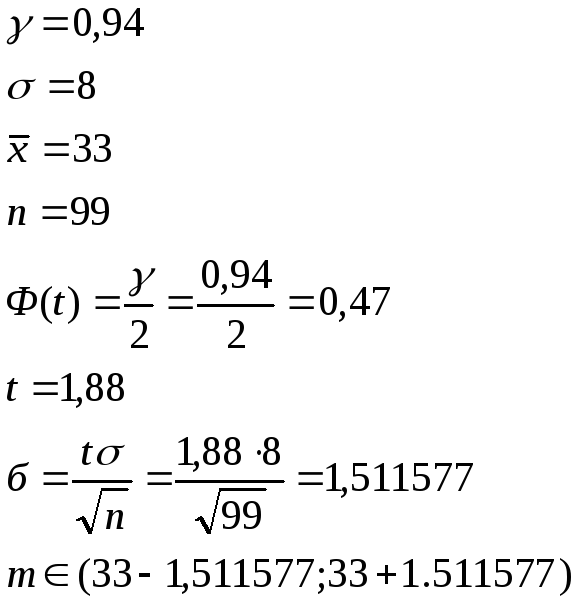
-
Выборка из большой партии электроламп содержит
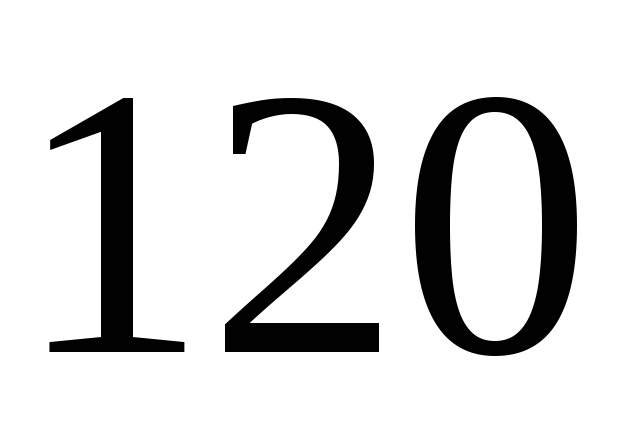 ламп. Средняя продолжительность горения
отобранных ламп оказалась равной
ламп. Средняя продолжительность горения
отобранных ламп оказалась равной
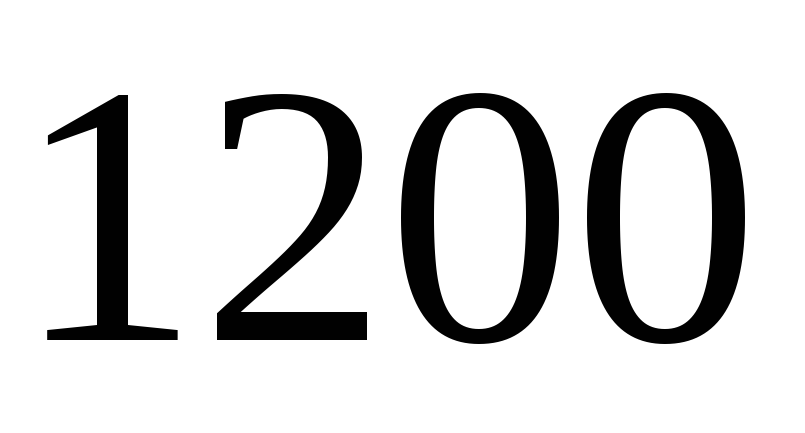 ч. Найдите приближенный
ч. Найдите приближенный
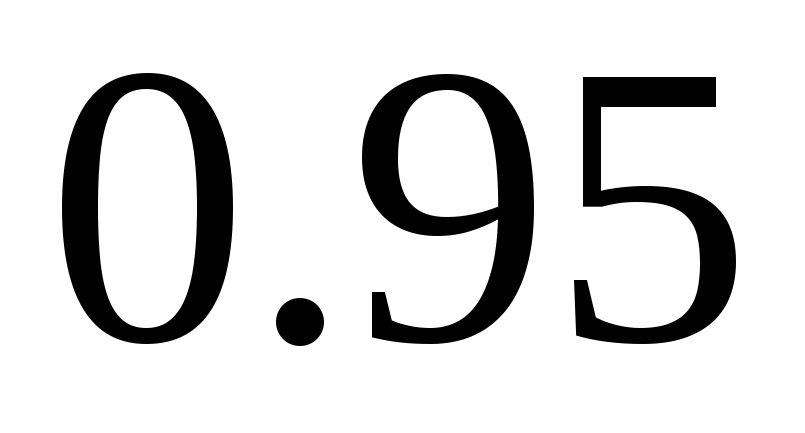 -доверительный
интервал для средней продолжительности
горения лампы во всей партии, если
известно, что среднеквадратичное
отклонение продолжительности горения
лампы в партии равно
-доверительный
интервал для средней продолжительности
горения лампы во всей партии, если
известно, что среднеквадратичное
отклонение продолжительности горения
лампы в партии равно
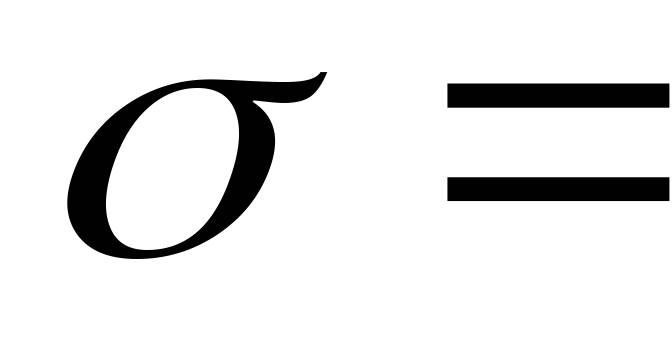
 ч.
ч.
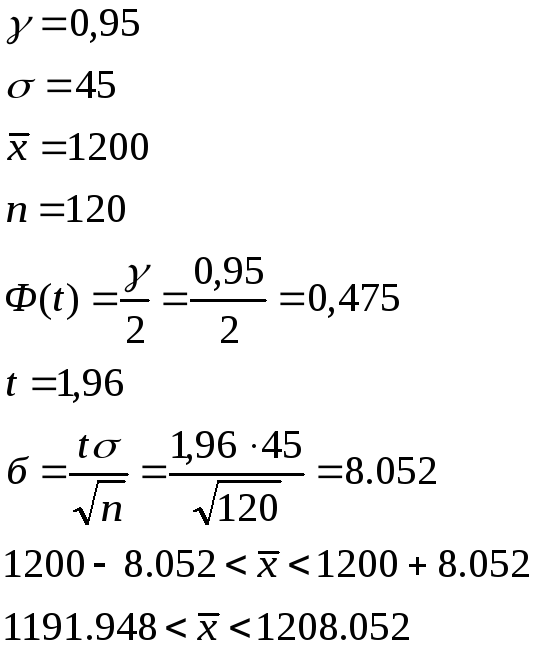
-
Произведено
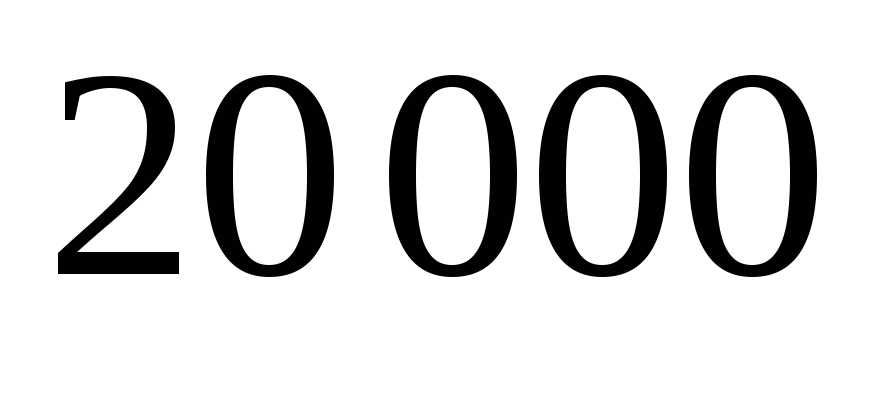 независимых испытаний, в каждом из
которых неизвестная вероятность
независимых испытаний, в каждом из
которых неизвестная вероятность
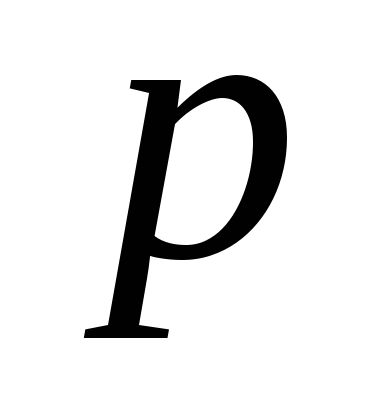 события
события
 постоянна. Событие
постоянна. Событие
 наступило в
наступило в
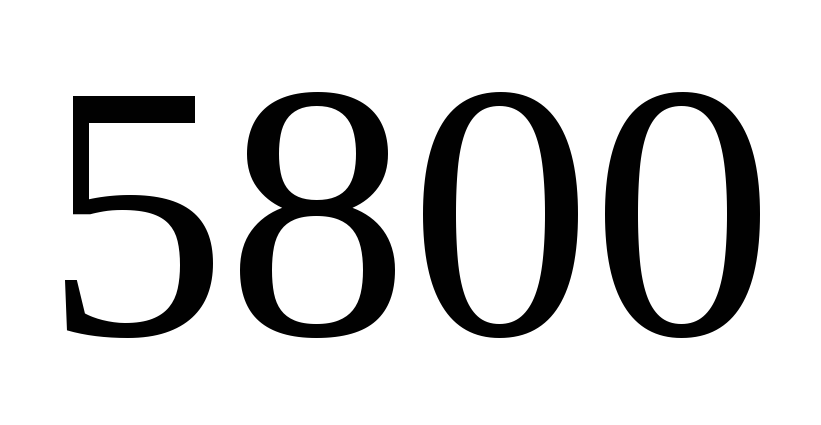 испытаниях. Найдите для вероятности
испытаниях. Найдите для вероятности
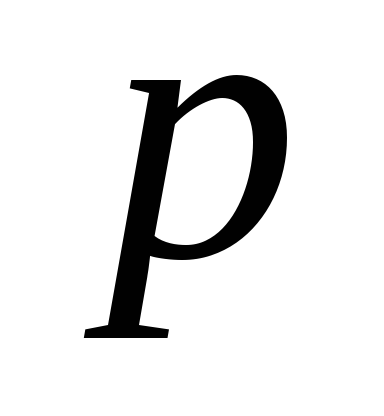 приближенный 0.994‑доверительный
интервал.
приближенный 0.994‑доверительный
интервал.
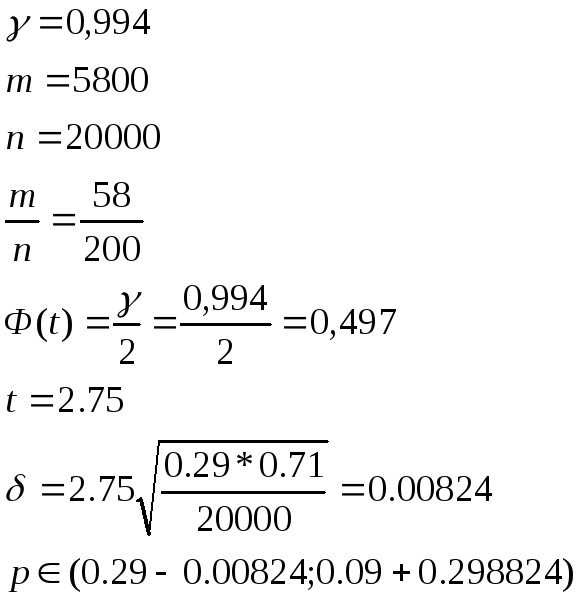
-
Выборочно обследовали качество кирпича. Из
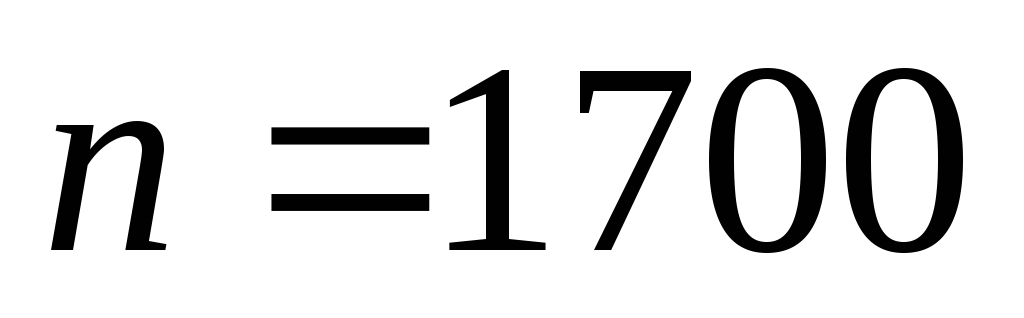 проб в
проб в
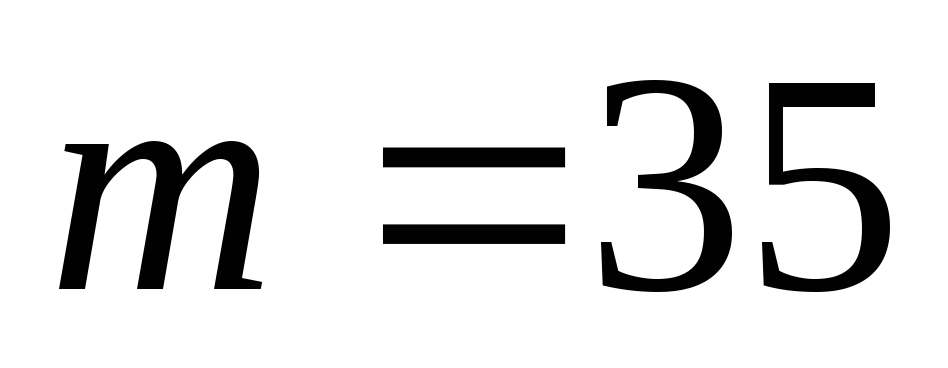 случаях кирпич оказался бракованным.
В каких пределах заключается доля брака
для всей продукции, если результат
гарантируется с надежностью
случаях кирпич оказался бракованным.
В каких пределах заключается доля брака
для всей продукции, если результат
гарантируется с надежностью
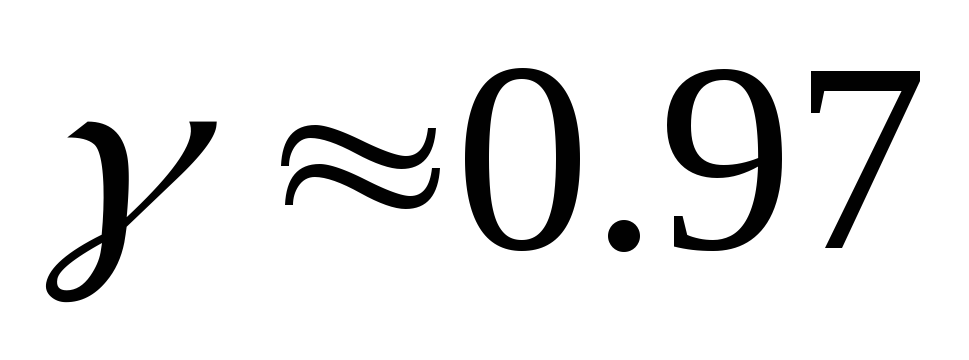 ?
?

-
При испытании
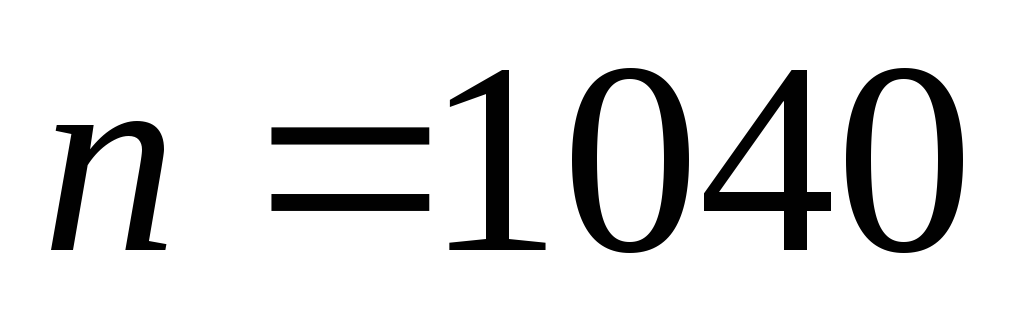 элементов зарегистрировано
элементов зарегистрировано
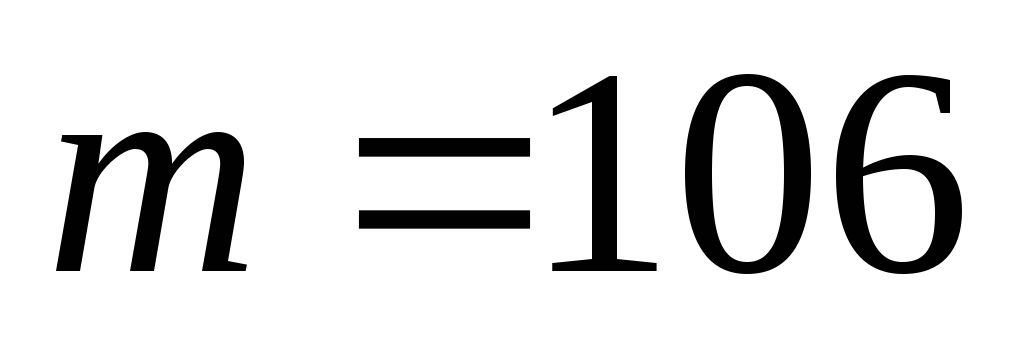 отказов. Найдите доверительный интервал,
покрывающий неизвестную вероятность
отказов. Найдите доверительный интервал,
покрывающий неизвестную вероятность
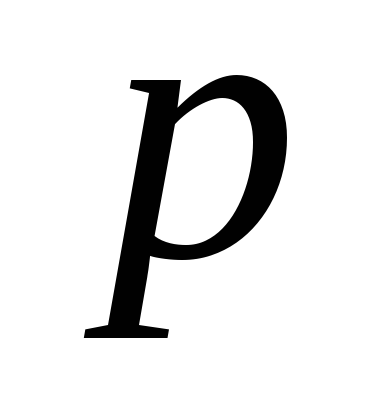 отказа элемента с надежностью
отказа элемента с надежностью
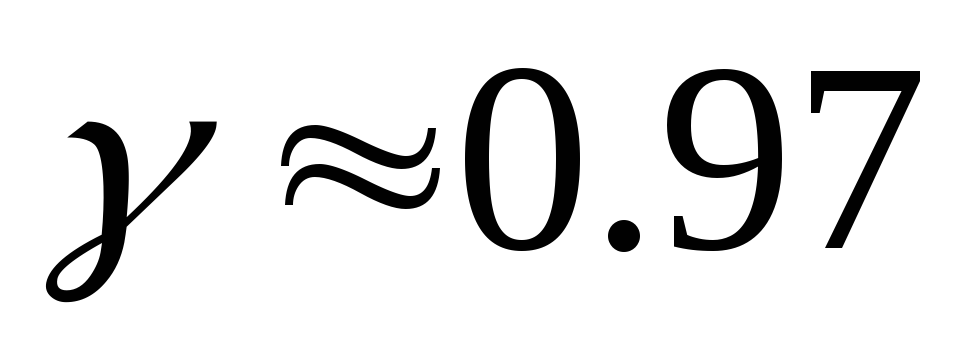 .
.
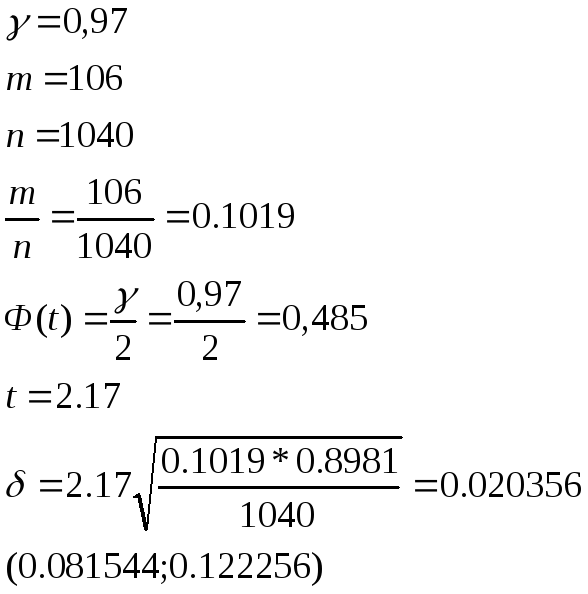
-
В результате проведенного социологического опроса
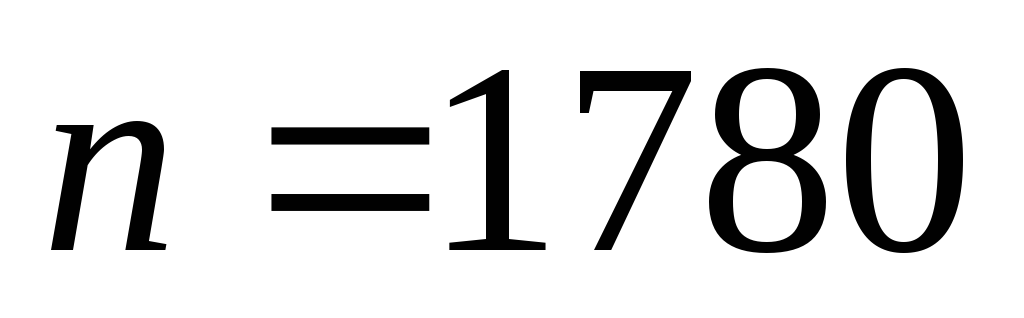 человек рейтинг кандидата в президенты
составил
человек рейтинг кандидата в президенты
составил
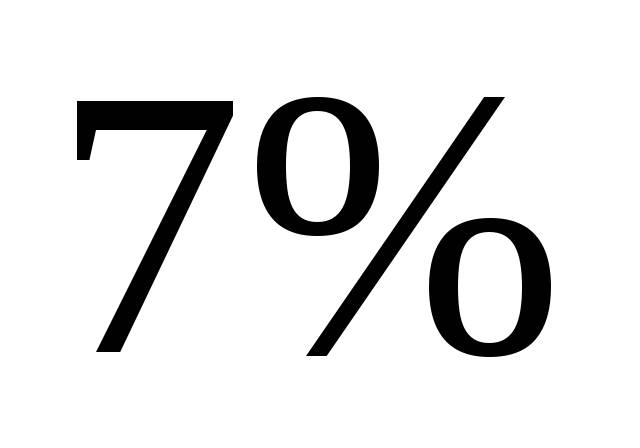 .
Найдите доверительный интервал для
рейтинга кандидата с гарантированной
надежностью
.
Найдите доверительный интервал для
рейтинга кандидата с гарантированной
надежностью
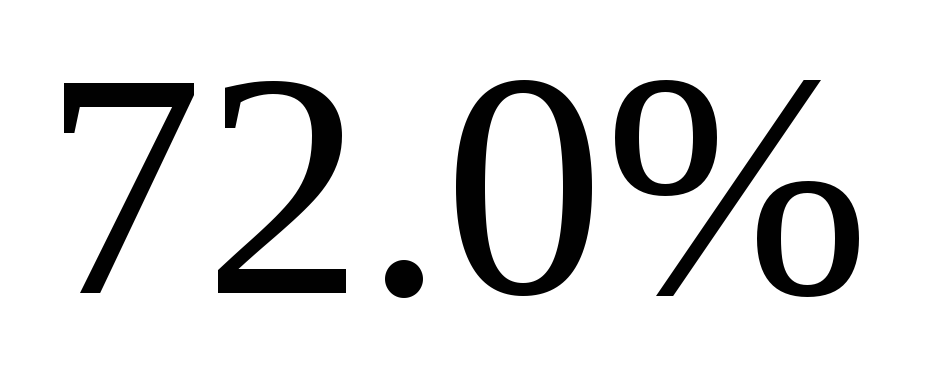 .
.

-
Численность повторной выборки составляет
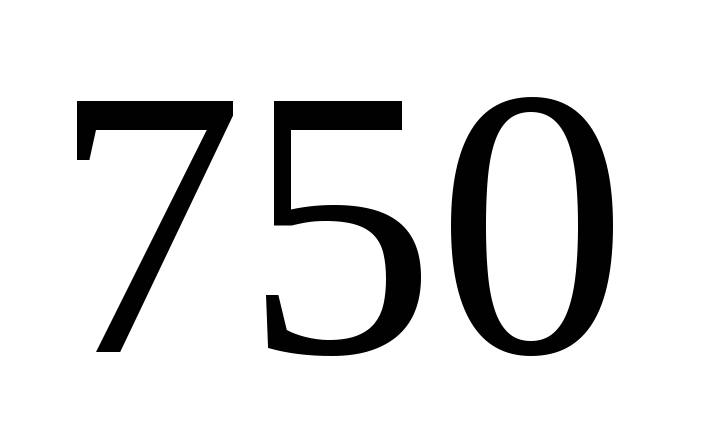 единиц. Доля признака составляет
единиц. Доля признака составляет
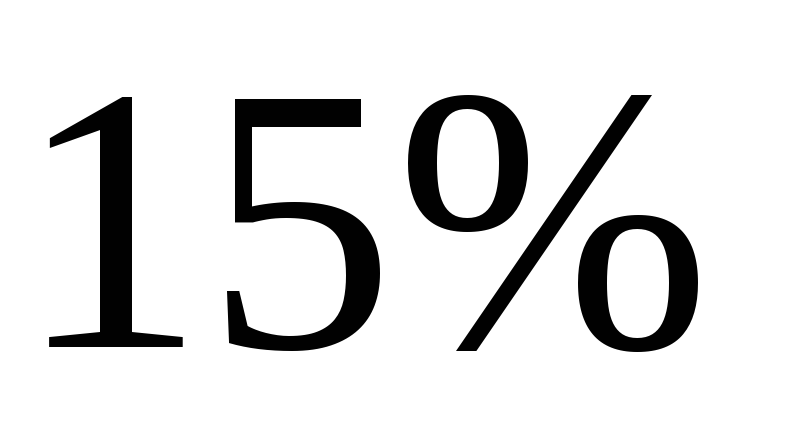 .
Найдите с доверительной вероятностью
.
Найдите с доверительной вероятностью
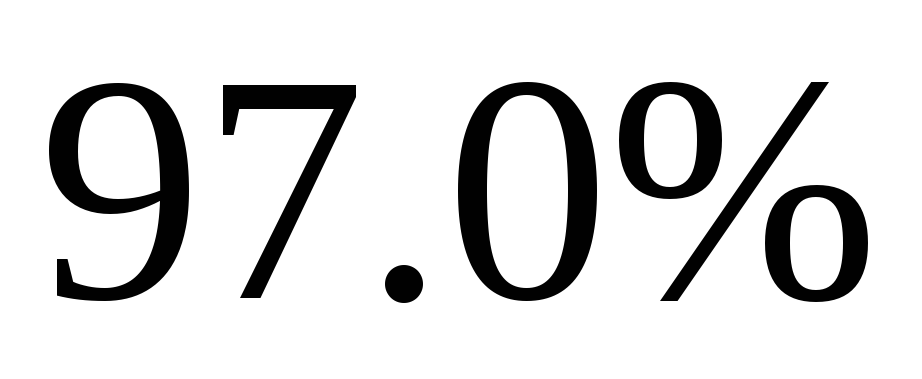 ,
в каких пределах находится отклонение
частоты от доли признака.
,
в каких пределах находится отклонение
частоты от доли признака.
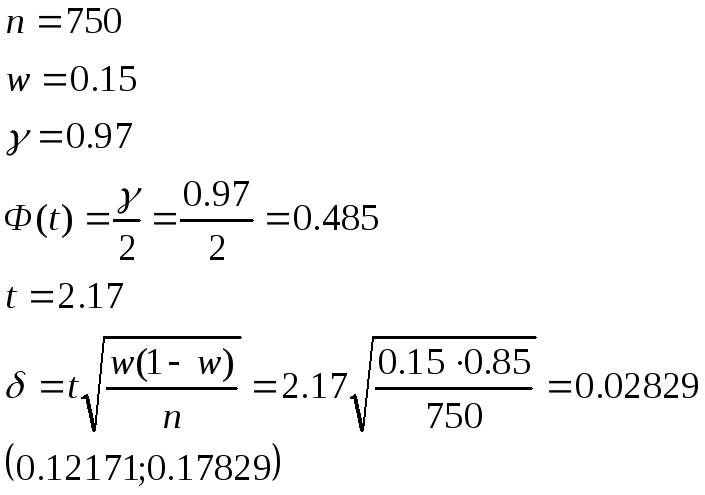
-
Обследуется средняя продолжительность телефонного разговора. Сколько телефонных разговоров должно быть зафиксировано, чтобы с вероятностью
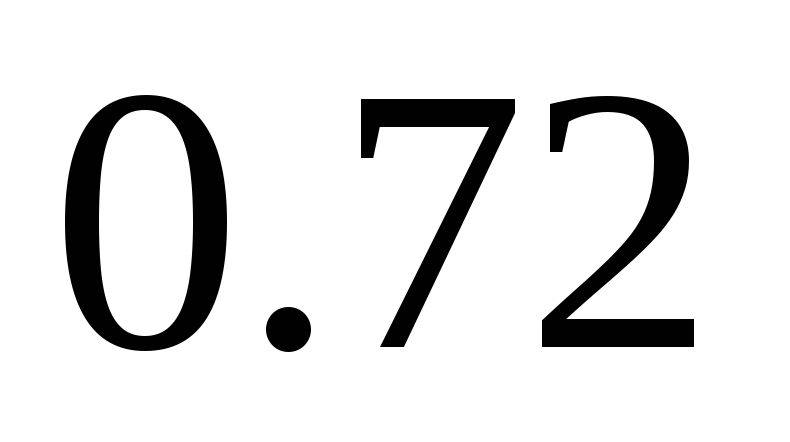 можно было бы утверждать, что отклонение
средней продолжительности зафиксированных
разговоров от генеральной средней не
превосходит
можно было бы утверждать, что отклонение
средней продолжительности зафиксированных
разговоров от генеральной средней не
превосходит
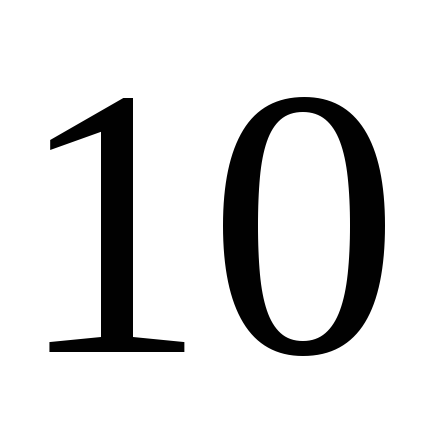 секунд, если среднее квадратичное
отклонение длительности одного разговора
равно
секунд, если среднее квадратичное
отклонение длительности одного разговора
равно
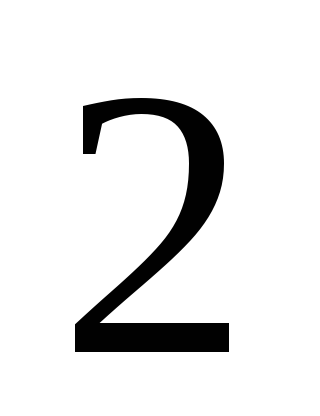 минутам?
минутам?
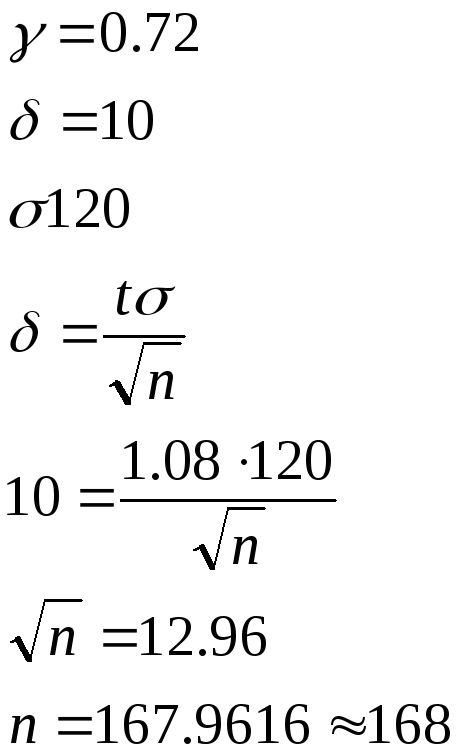
-
Производится выборочное обследование возраста читателей массовых библиотек. Сколько карточек необходимо взять для обследования, чтобы с вероятностью
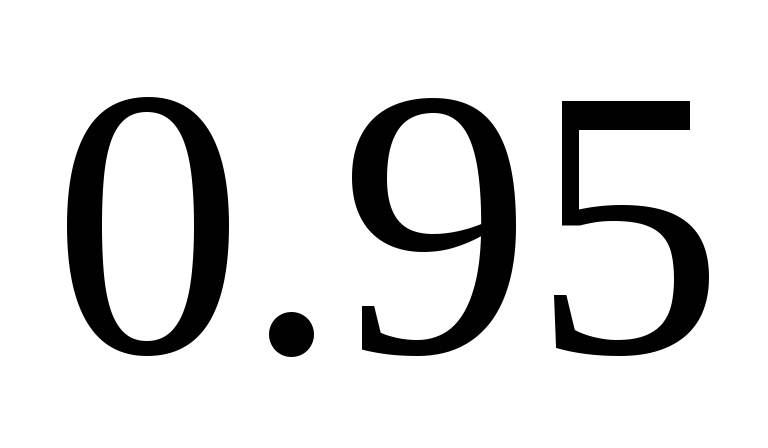 можно было бы утверждать, что средний
возраст в выборочной совокупности
отклонится от генерального среднего
не более, чем на 2 года? Генеральное
среднее квадратичное принять равным
можно было бы утверждать, что средний
возраст в выборочной совокупности
отклонится от генерального среднего
не более, чем на 2 года? Генеральное
среднее квадратичное принять равным
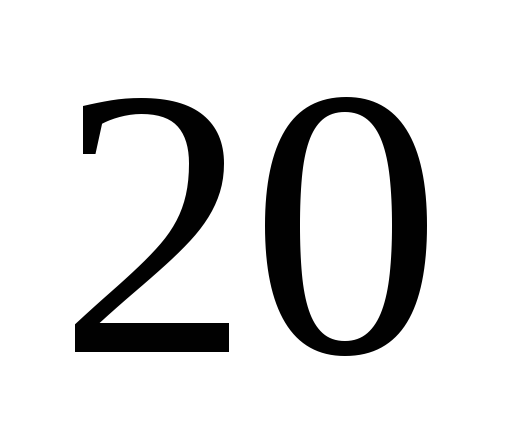 годам.
годам.