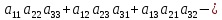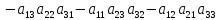- •Матрицы и действия над ними.
- •Понятие определителя и его свойства. Вычисление определителя с помощью метода Сарруса.
- •Обратная матрица. Алгоритм нахождения.
- •Применение обратной матрицы для решения систем линейных уравнений, матричные уравнения.
- •Действия над векторами в координатах.
- •Разложение вектора в базисе, скалярное произведение и его свойства.
- •Уравнения линий второго порядка.
- •Числовая функция, способы задания, свойства, графики, преобразование графиков.
- •Производная сложной и обратной функции, приложение производной к решению задач.
- •Дифференциал, его геометрический смысл, вычисление дифференциала сложной функции.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Определение и геометрический смысл определенного интеграла. Формула Ньютона – Лейбница для вычисления площади криволинейной трапеции.
- •Определение несобственного интеграла и его вычисление.
- •Дифференциальные уравнения и их решение.
- •Интегрирование по формулам прямоугольников и трапеций.
-
Матрицы и действия над ними.
Ответ:
Матрица – прямоугольная таблица чисел, расположенных в n строках и m столбцах. A = (i,j) где i – номер строки, j – номер столбца.
Размерность матрицы – число строк и число столбцов в данной матрице.
Квадратная
матрица
– матрица, когда у нее число строк и
число столбцов равны.
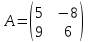
Главная диагональ – диагональ, идущая из верхнего левого до правого нижнего угла.
Побочная диагональ – диагональ, идущая из верхнего правого до нижнего левого угла.
Матрица, у которой все элементы нули называют нулевой матрицей. А = ( 0 0 )
Диагональная
матрица –
матрица, у которой элементы расположенные
вне главной диагонали нули.
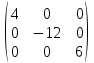
Умножение
матрицы на число подчиняется следующим
законам:
Единичная
матрица –
диагональная матрица, в которой элементы
главной диагонали равны 1.
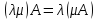 -ассоциативный
закон относительно числового
множества
-ассоциативный
закон относительно числового
множества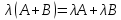 -распределительный
(дистрибутивный) закон относительного
множества
-распределительный
(дистрибутивный) закон относительного
множества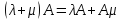 – дистрибутивный
закон относительно суммы числовых
множителей
– дистрибутивный
закон относительно суммы числовых
множителей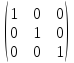
Действия над матрицами.
-
Умножение матрицы на число.
Любую матрицу можно умножить на число.
Для этого каждый элемент матрицы умножается на число.
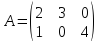
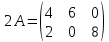
Свойства
сложения матриц:
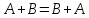 – переместительный(коммуникативный)
закон
– переместительный(коммуникативный)
закон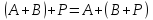 – сочетательный
(ассоциативный) закон
– сочетательный
(ассоциативный) закон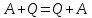 – где Q-нулевая
матрица соответствующего размера
– где Q-нулевая
матрица соответствующего размера
-
Сложение матриц.
Любые две матрицы одних и тех же размеров можно сложить. Получится матрица в точности тех же размеров.
Пусть
А =
 и
и
В =
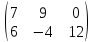 ,
то A+B=
,
то A+B=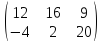
-
Свойства произведения матриц:
-
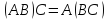 -
ассоциативность
-
ассоциативность -
 – ассоциативность
по умножению
– ассоциативность
по умножению -
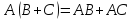
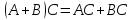
-
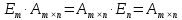 – умножение на
единичную матрицу
– умножение на
единичную матрицу
-
Матрицу А можно умножать на матрицу В, если количество столбцов А равно количеству строк В.
Пусть
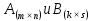 ,
то
,
то
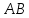 возможно только если
возможно только если
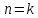 .
При этом в результате получится матрица
C
размерами
.
При этом в результате получится матрица
C
размерами
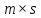 .
.
Пусть
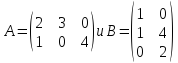 , то
, то
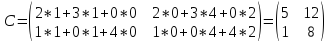
Так произведение
BA
существует и равно
 .
.
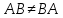 следовательно,
умножение матриц некоммутативно,
т.е. зависит от порядка сомножителя.
следовательно,
умножение матриц некоммутативно,
т.е. зависит от порядка сомножителя.
-
Свойства транспонирования:
-
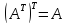 3)
3)
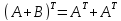
-
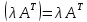 4)
4)
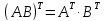
-
Транспонирование – это операция над матрицами, когда ее строки становятся столбцами с теми же номерами.
Пусть
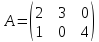 ,
то транспонированная матрица
,
то транспонированная матрица
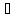
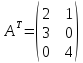 .
.
-
Понятие определителя и его свойства. Вычисление определителя с помощью метода Сарруса.
Ответ:
Квадратная матрица A n-го порядка характеризуется неким числом называемым определителем.
Обозначается: detA
Свойства определителей:
-
Определитель не изменится, если в нем строки и столбцы поменять местами.
-
Определитель изменит знак, если в нем поменять местами какие-нибудь 2 строки или 2 столбца.
-
Общий множитель элементов строки или столбца можно выносить за символ определителя.
-
Определитель равен нулю, если элементы двух строк или столбцов пропорциональны.
-
Определитель равен нулю, если он имеет 2 одинаковых строки или 2 одинаковых столбца.
-
Если все элементы некоторой строки или столбца состоят из 2 слагаемых, то определитель можно представить в виде суммы 2 определителей, в одном из которых элементами соответствующей строки являются первые слагаемые, во втором - вторые.
-
Если к элементам некоторого столбца или строки определителя прибавить соответствующие элементы другого столбца или строки, умноженные на общий множитель, то величина определителя не изменится.
Правило Сарруса:
 =
=