1.2. Скорость фильтрации. Истинная или действительная средняя скорость движения частицы

Рассмотрим модель пористой среды пласта или так называемую трубку тока (рис. 1.3), площадь поперечного сечения которой f, давления на концах модели Р₁ и Р₂. Пусть Р₁>Р₂ . Под действием разности давлений Р=Р₁–Р₂ жидкость начинает двигаться. Однако жидкость будет двигаться не через всю площадь сечения f, а только через площадь просветов f_пр, которую называют живым сечением потока. Исходя из теории статистики, можно считать, что в любом сечении трубки f_пр будет иметь одинаковое значение.

Рис. 1.3. Модель пористой среды пласта

(трубка тока постоянного сечения)

Если Q – объемный расход жидкости через модель с перепадом давления Р, тогда скорость фильтрации  определяется из соотношения

(1.11)

Очевидно, скорость фильтрации не является действительной средней скоростью движения в живом сечении. Последняя будет больше скорости фильтрации и и определится из соотношения

(1.12)

Установим связь между  и u . Пусть dx – расстояние между двумя сечениями, dt – время, за которое жидкость из одного сечения переместилась в другое. Объем жидкости, вытесненной из области dx, можно определить из соотношения

dV=Qdt=mfdx.

Отсюда следует:

или  =mu. (1.13)

Подставляя (1.11), (1.12) в (1.13), получим

или (1.14)

1.3. Линейный закон фильтрации Дарси. Коэффициенты фильтрации и проницаемости

Одним из основных законов теории фильтрации является линейный закон Дарси (1856), объясняющий связь между потерей напора (Н₁–Н₂) и объемным расходом Q жидкости, текущей в трубке тока постоянного сечения f (рис. 1.4.).

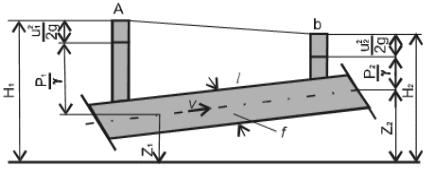
Рис. 1.4. Схема опыта Дарси

Дарси установил, что расход жидкости через трубку с пористой средой прямо пропорционален потере напора и площади фильтрации f и обратно пропорционален длине трубки l, т. е.

(1.15)

где

(1.16)

Н – напор в любом сечении;

Z – высота положения;

 – пьезотермическая высота;

 – скоростной напор (высота);

С – коэффициент фильтрации;

 – объемный вес жидкости.

Скоростным напором обычно пренебрегают.

Потеря напора на единицу длины называется гидравлическим уклоном, т. е.

(1.17)

Таким образом,

или (1.18)

Так как i – безразмерная величина, коэффициент фильтрации имеет размерность скорости [C]=см/с.

Коэффициент С характеризует как пористую среду, так и жидкость, а формулы (1.18) и (1.15) хорошо удовлетворяют теории фильтрации воды. В теории фильтрации нефти и газа закон Дарси записывается по иному:

(1.19)

или

(1.20)

Здесь

K – коэффициент проницаемости;

 – коэффициент абсолютной вязкости;

Р=Н – приведенное давление.

Сравнивая (1.19) и (1.20), находим связь

(1.21)

Закон Дарси может быть записан и в дифференциальной форме. Возьмем трубку тока переменного сечения (рис. 1.5). Отсчет будем вести от точки О. Проведем два сечения на расстоянии S и dS от начала отсчета. В общем случае имеем Н=Н(S, t), для установившегося движения Н=Н(S).

Рис. 1.5. Схема фильтрационного потока в трубке