6.3. Второй закон Кеплера
Радиус-вектор планеты в равные промежутки времени описывает равновеликие площади.
Этот закон указывает на неравномерность движения КА по эллиптической орбите. Схема, иллюстрирующая второй закона Кеплера, приведена на рис. 4.6.2.
Рис. 6.2. Схема для иллюстрации второго закона Кеплера
На этом рисунке
площади
,
и
,
описываемые радиусом-вектором за равные
промежутки времени
,
равны. Следовательно, неравны длины
путей на этих участках:
.
В последующие годы второй закон Кеплера был получен из так называемого интеграла площадей или закона сохранения момента импульса:
,
или
в скалярной форме (для постоянной массы):
.
Рассмотрим частный случай
В точках апогея и
перигея углы
равны нулю (см. рис. 6.3), следовательно,
из закона сохранения площадей
.
Откуда:
.
(6.1)
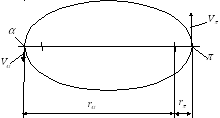
Рис. 6.3. Схема для расчета соотношения скоростей КА в апогее и перигее эллиптической орбиты
То есть, отношение скоростей в апоцентре и перицентре обратно пропорциональны отношению модулей радиусов-векторов.
Рассмотрим конкретный пример.
Пусть
км (высота перигея орбиты в 200 км, радиус
Земли 6371 км),
км/с,
км (высота апогея орбиты 36000 км).
Определить скорость КА в апогее.
Решение. Из соотношения (6.6.1) можно получить
км/с.
6.4. Третий закон Кеплера
Квадраты периодов обращения планет вокруг Солнца прямо пропорциональны кубам больших полуосей их орбит.
(6.2)
или
Пример.
Для Земли
Млн. км; для Марса
Млн. км (см. рис. 6.4).
Найти отношение периодов обращения.
Из формулы (4.6.2) можно получить
(земных года).
Рис. 6.4. Схема для иллюстрации третьего закона Кеплера
Абсолютное время периода обращения тела, движущегося вокруг притягивающего центра можно получить по следующей зависимости (приводится без вывода):
.
6.5. Параметры орбиты в пространстве
Положение КА на орбите иллюстрируется рисунком 6.5 и характеризуется следующими параметрами:
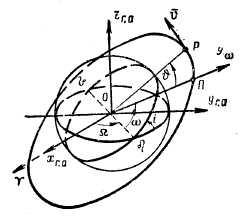
Рис. 6.5. Элементы орбиты в пространстве (а) и на плоскости (б)
- долгота восходящего
узла — угол, расположенный в экваториальной
плоскости и отсчитываемый от направления
на точку весеннего равноденствия (знак
Овен, ось Ох) до линии узлов т. е.
линии пересечения плоскости орбиты с
плоскостью экватора; восходящим узлом
орбиты называют точку, в которой тело
переходит из южного полушария в северное;
противоположная точка называется
нисходящим узлом.
i
— наклонение
орбиты — двугранный угол между плоскостью
орбиты и плоскостью экватора, отсчитываемый
от плоскости экватора против хода
часовой стрелки для наблюдателя,
находящегося в точке восходящего узла.
— аргумент перигея — угловое расстояние
перицентра П от восходящего узла,
отсчитываемое в плоскости орбиты в
направлении движения.
u — аргумент широты — центральный угол, отсчитываемый в плоскости орбиты в направлении движения от восходящего узла до радиуса-вектора движущейся точки Р.
— аргумент перигея;
Аргумент широты связан с аргументом перигея и истинной аномалией следующим соотношением
.
t — момент прохождения КА через перицентр.