Самарский государственный аэрокосмический университет

имени академика С.П.Королева

Кафедра летательных аппаратов

Лабораторная работа

по дисциплине

«Введение в специальность 230301-

Моделирование и исследование операций

в организационно-технических системах»

Моделирование движения космических аппаратов

Разработал В. И. Куренков

Самара 2007

Цель работы: Изучение некоторых законов небесной механики.

Задание:

1.Изучить теоретическую часть данной темы.

2. Проанализируйте и решите задачи из вариантов задания, приведенных в конце методических указаний.

3. Оформите отчет в текстовом редакторе Word в соответствии с СТП СГАУ по оформлению учебных текстовых документов.

4. Отчитайтесь преподавателю, ответив устно на некоторые контрольные вопросы по теоретической части.

Методические указания

Расчетную часть можно проводить по выбору студента с использованием калькулятора, табличного процессора Excel или математической системы Mathcad.

В отчете должны быть приведены исходные данные для расчета, расчетные схемы, расчетные зависимости. В тексте отчета должны быть необходимые пояснения производимых расчетов.

В задачах, не требующих расчета следует привести текстовое описание ответа.

Дополнительное задание (для студентов, выполнивших основное задание)

1. Постройте графики периодов обращения КА, находящихся на орбитах с различными эксцентриситетами.

2. Постройте графики периодов обращения КА, находящихся на орбитах с различными радиусами перигея.

3. Постройте графики периодов обращения КА, находящихся на орбитах с различными эксцентриситетами и радиусами перигея.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

6.1. Закон всемирного тяготения

Сила, с которой притягиваются два тела с массами и пропорциональна произведению этих масс и обратна пропорциональна квадрату расстояния r между ними.

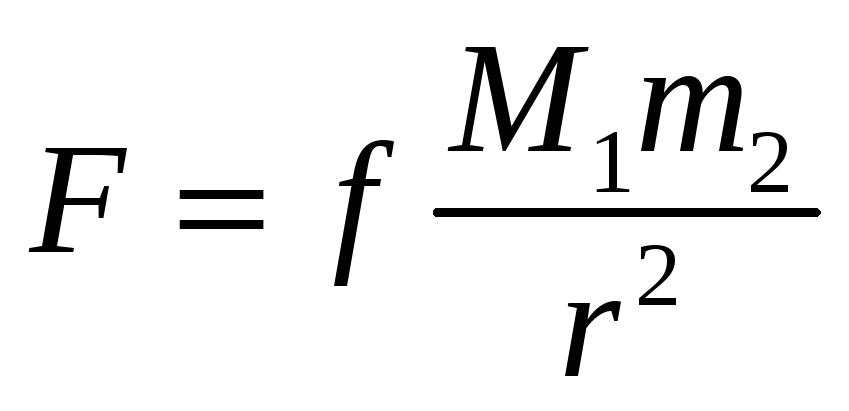, где - коэффициент пропорциональности (гравитационная постоянная);

Параметр называют гравитационной постоянной притягивающего центра с массой . Например для Земли этот параметр составляет ; для Солнца .

6.2. Первый закон Кеплера

Иоганн Кеплер (1571-1670).

Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

В последующие годы первый закон Кеплера был также получен на основе закона сохранения энергии в центральном поле тяготения. Было показано, что этот закон справедлив для космических аппаратов, движущихся вокруг Земли, и вообще для любых тел, движущихся в центральном поле тяготения по замкнутым орбитам.

Характеристики орбит космических аппаратов

Положение КА на орбите (в плоскости ) иллюстрируется рисунком 4.6.1.

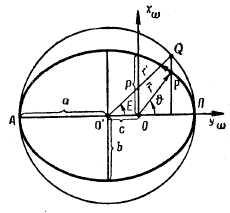
Рис. 6.1. Элементы орбиты на плоскости

Положение КА на орбите характеризуется следующими параметрами:

r — радиус-вектор, направленный из притягивающего центра в движущуюся точку Р;

— угол истиной аномалии (или просто истинная аномалия);

Е — эксцентрическая аномалия — угол, отсчитываемый от положительного направления оси до радиуса вспомогательной окружности, проведенного в точку пересечения Q окружности с перпендикуляром к оси , проходящим через движущуюся точку Р на эллипсе;

а — большая полуось (среднее расстояние движущейся точки от притягивающего центра);

b - малая орбиты;

с — сжатие орбиты;

р — фокальный параметр - высота перпендикуляра к большой оси эллипса, восстановленного из фокуса, где находится притягивающее тело, до пересечения с орбитой;

П — перицентр (перигей, перигелий, периселений и т.п.);

- радиус перицентра орбиты – расстояние от притяг центра до перицентра;

А - апоцентр (апогей, апогелий, апоселений и т.п.);

- радиус апоцентра орбиты - расстояние от притяг центра до апоцентра;.

Из схемы видно, что

.

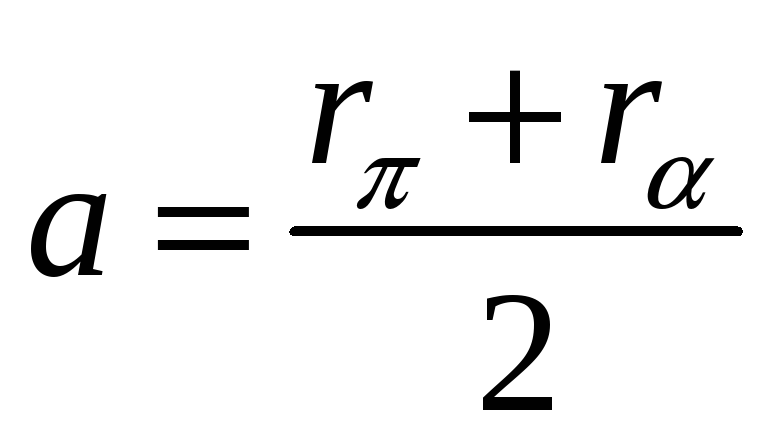Эксцентриситет орбиты есть отношение расстояния между центром орбиты О' и ее фокусом О к большой полуоси:

.

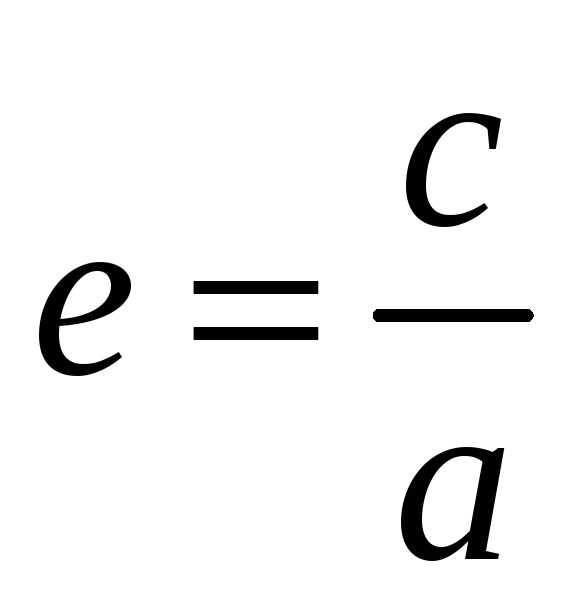Радиусы апоцентра и перицентра связаны с эксцентриситетом следующими зависимостями:

;

.

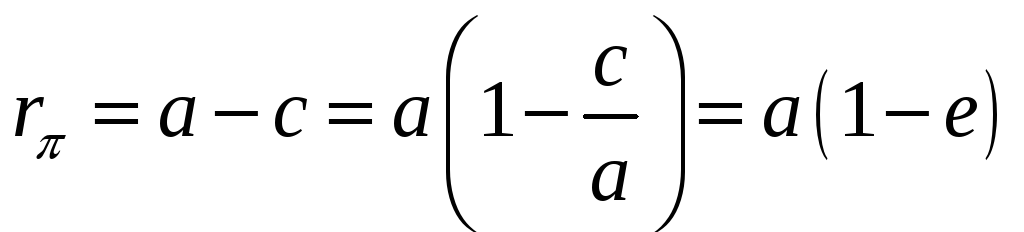Уравнение эллиптической орбиты в декартовых координатах:

.

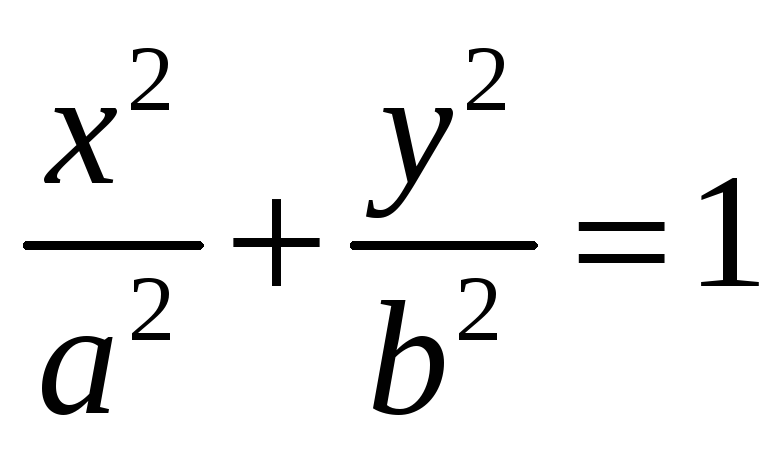Однако удобнее пользоваться уравнением эллиптической орбиты в полярных координатах:

.

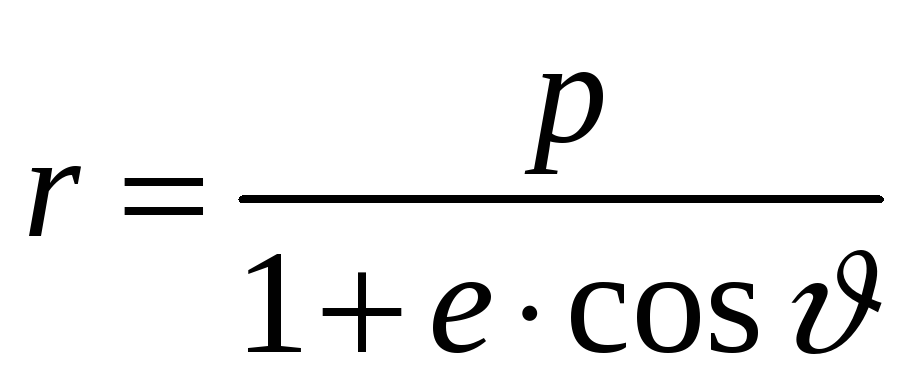В точках перицентра и апоцентра углы равны соответственно 0 и 180 градусов. Подставляя эти углы в последнее выражение можно получить:

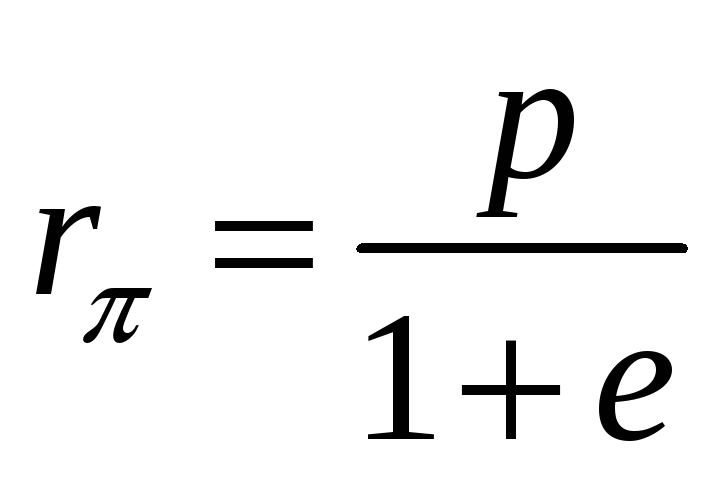и .

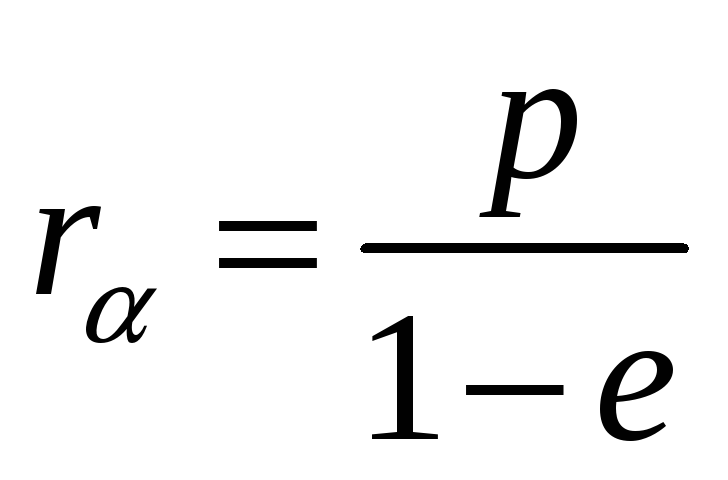Откуда можно получить значение фокального параметра:

или .

Из последнего выражения можно получить

.
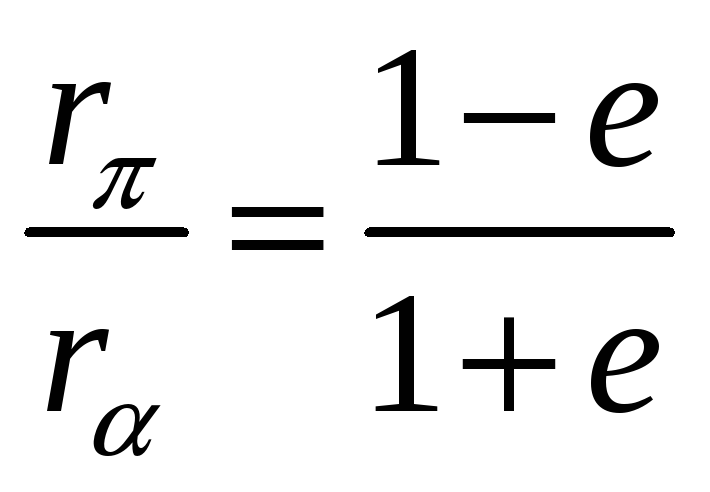