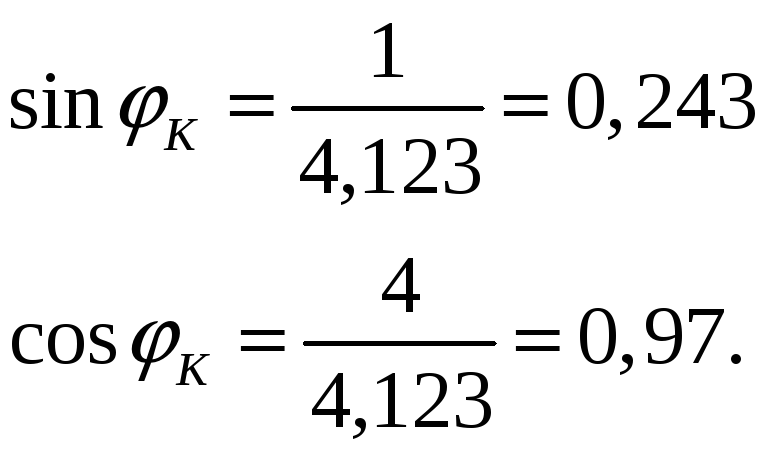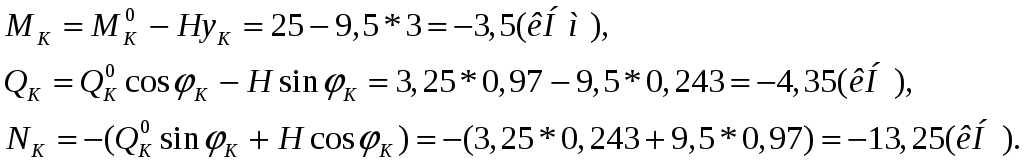Распорные системы.

Распорные системы – это системы, в которых под действием внешней нагрузки возникает наклонная опорная реакция с горизонтальной составляющей, называемой распором.

К ним относятся: арки, рамы, комбинированные и вантовые системы.

Двухшарнирная арка – криволинейная конструкция с 2-мя неподвижными опорами А и В, называемыми пятовыми.

Это статически – неопределимая система.

Если поставить в середину дополнительный шарнир «С» (ключевой шарнир), то арка станет трехшарнирной.

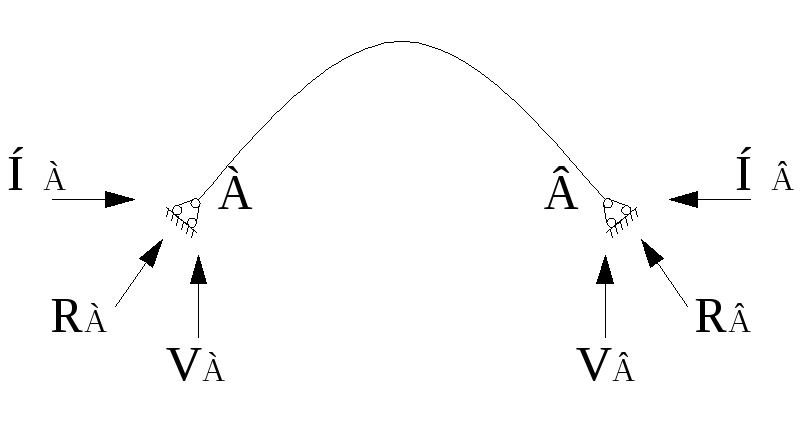
Трехшарнирная арка – статически определимая и геометрически неизменяемая конструкция, состоящая из 2-х полуарок, имеющую наклонную реакцию в неподвижных шарнирах А и В.

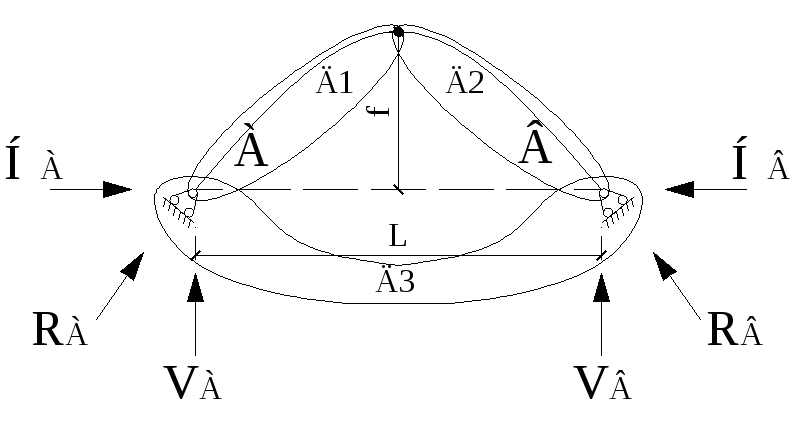
f – стрела подъема (расстояние по нормали от ключевого шарнира до линии, соединяющей опорные шарниры);

l – пролет (расстояние между неподвижными опорами);

АС и СВ – полуоси арки.

Кинематический анализ. D₁, D₂, D₃, соединены по 4 типу.

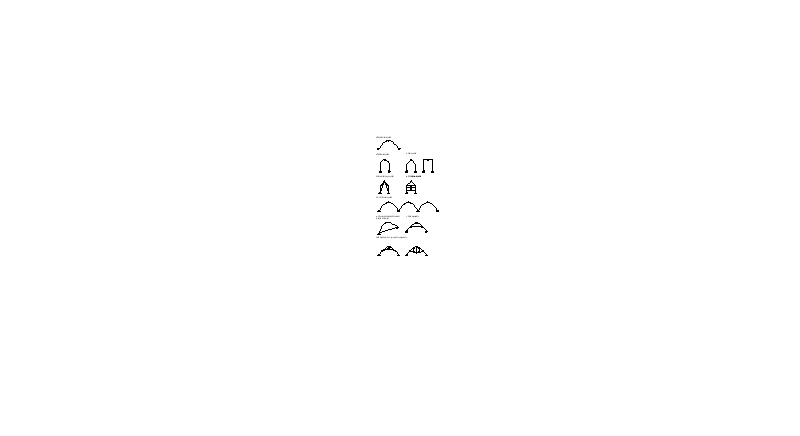
Виды арок.

Определение опорных реакций трехшарнирной арки.

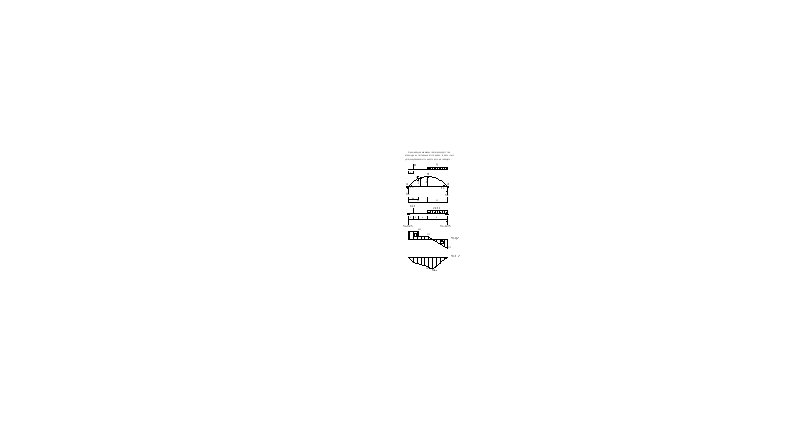
Вертикальные составляющие опорных реакций арки равны соответствующим опорным реакциям эквивалентной балки:

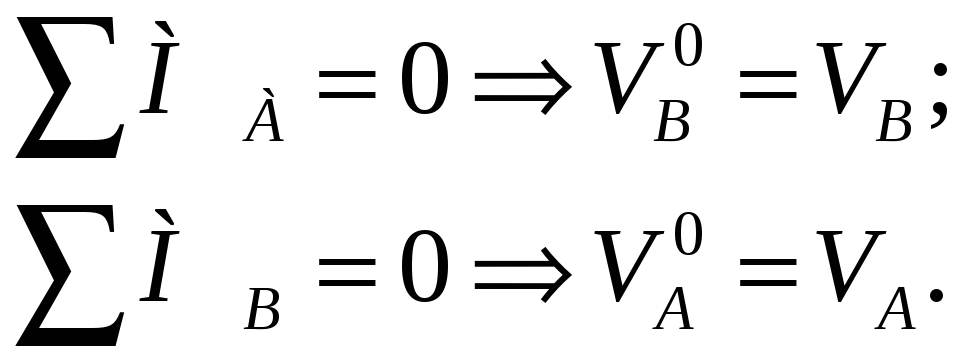(1)

Горизонтальная составляющая или распор определяется из уравнения:

Чтобы определить ее величину, воспользуемся дополнительным уравнением: сумма момента левее или правее ключевого шарнира С равна нулю.

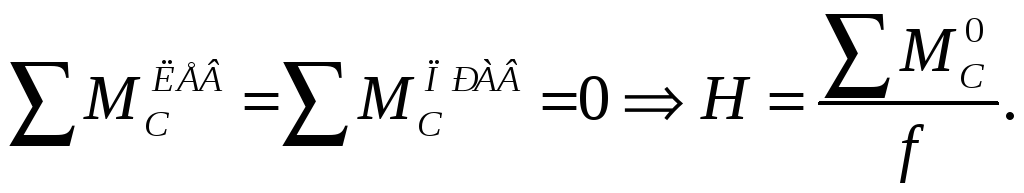(2)

Особенности формулы 2:

- Н не зависит от вида арки,

- при .

- при .

Пример.

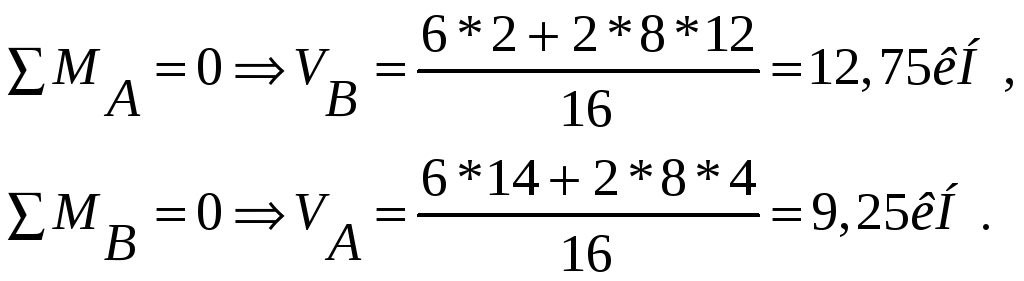
Проверка: 9,25+12,75=6+2*8

0=0.

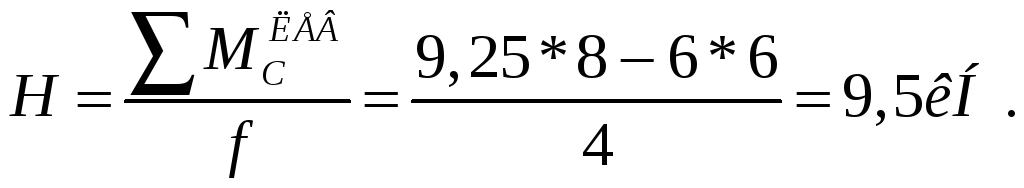
Строим эпюры Q⁰ и М⁰.

Определение внутренних усилий в заданном сечении арки.

Внутренними усилиями является изгибающий момент М_К, поперечная сила Q_К и продольное усилие N_К, которые определяются методом сечений из соответствующих уравнений равновесия.

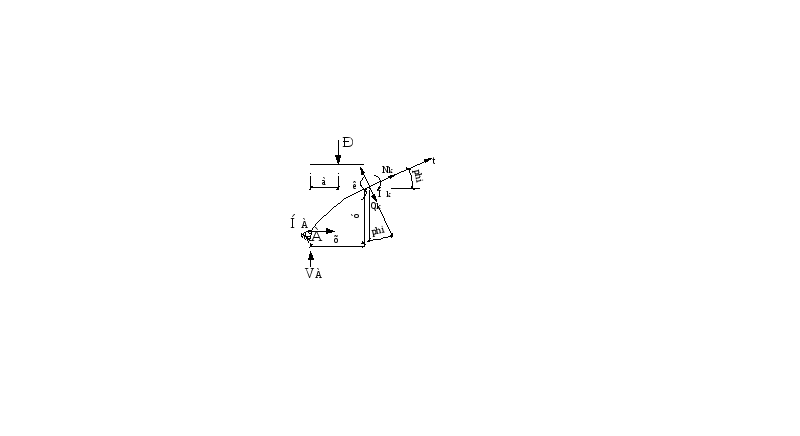
М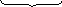_К = V_Ax_K - P(x_K-a) - Hy_K, где х_К и у_К – координаты сечения «к».

М_К⁰

М_К= М_К⁰- Hy_K. (3)

Из (3) видно, что:

- М_К не зависит от вида арки;

- Арка экономичнее балки, так как М_К арки < М_К⁰ балки на Hy_K.

Найдем Q_К из рассмотрения равновесия всех сил левее сечения на нормаль «n» к оси. Пусть - угол наклона касательной в сечении «К» к оси «Х».

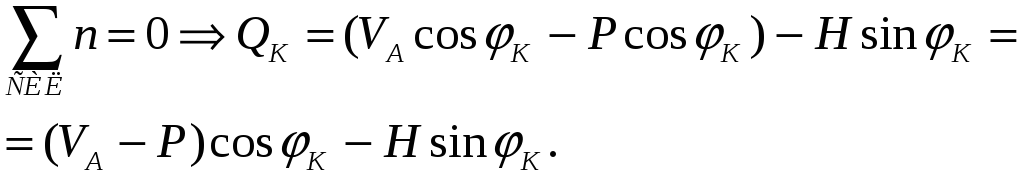
(4)

Аналогично, рассматривая равновесие всех сил левее сечения на ось «t» перпендикулярной «n», найдем продольное усилие N_K:

(5)

Из (5) видно, что продольные усилия в сечении арки всегда сжатые (N<0).

Замечания к формулам (3) – (5):

1. С ниспадающей стороны арки ,

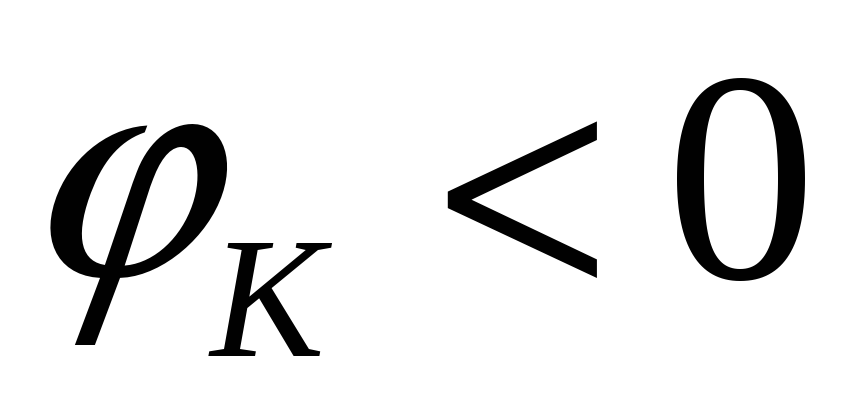значит

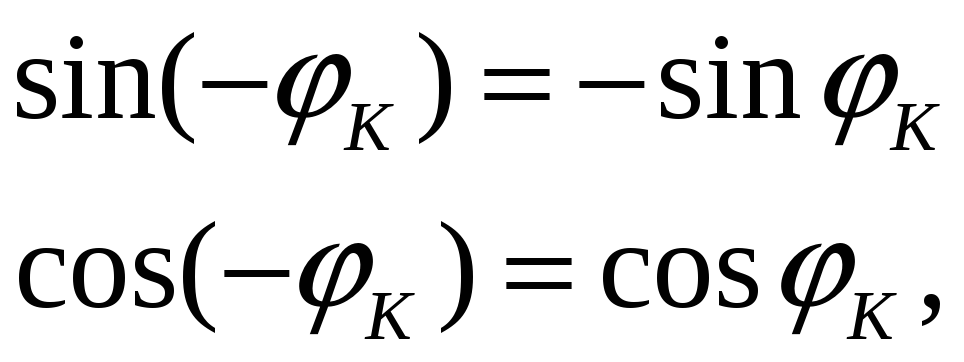
поэтому получим:

(4^l)

(5^l)

2. Если сечение находится в месте соединения двух панелей арки, то нужно определять Q_K^лев; N_K^лев и Q_K^пр; N_K^пр.

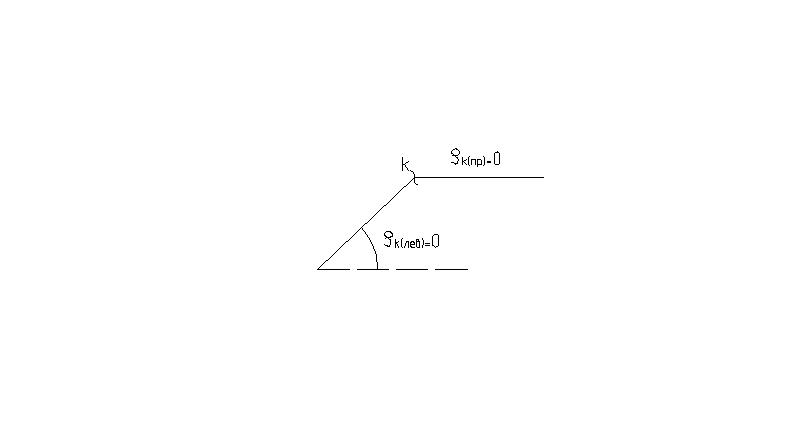
Пример.

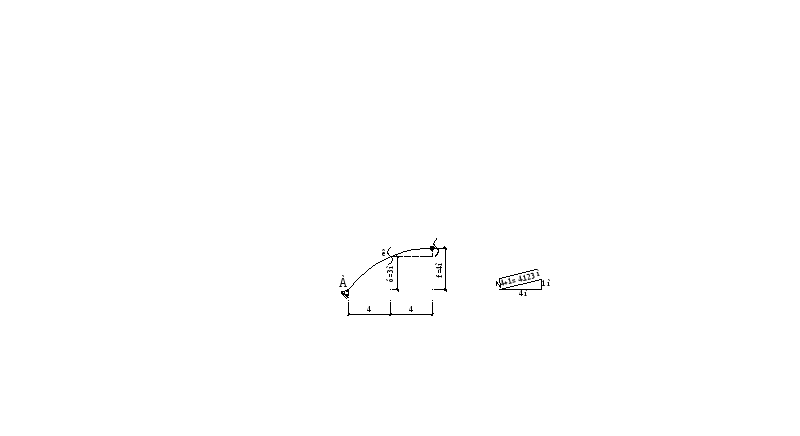
Найдем М_К; Q_K; N_K.

С эпюры Q⁰ возьмем Q_К⁰ = 3,25 кН.

М_К⁰ = 9,25*4 – 6*2 = 25 кНм.

у_К = 3 м.

х_ч = 4 м.

Н = 9,5 кН.