
5.2 Синтез дискретного корректирующего звена
Так как в данной САУ предусматривается установка цифрового микроконтроллера, который может осуществлять вычисление сигнала рассогласования, а при необходимости реализовывать программную коррекцию системы, то следует рассчитать программное корректирующее устройство.
Выберем интервал опроса датчиков (период дискретизации) 0.001 с для того чтобы обеспечить выполнение требуемого закона управление за время переходного процесса 0.04 с
Перейдем от непрерывной модели объекта к дискретной с интервалом дискретизации 0.001 c, используя экстраполятор нулевого порядка, для этого воспользуемся в программе MATLAB функцией преобразования непрерывной модели системы в дискретную (с2d) [7].
Ts=0.001;Wdis=c2d(Wp,Ts,'zoh') , получим передаточную функцию разомкнутой дискретной системы:
Умножая числитель и знаменатель выражения (43) на z-1, получим
![]() . (44)
. (44)
Выражение (44) является передаточной функцией дискретного последовательного корректирующего устройства в формате цифрового фильтра. При этом множитель z-1=e-pT, представляет собой оператор задержки, то есть
z-1*Uk=Uk-1, z-2*Uk=Uk-2 и т. д.
Аналоговые фильтры, как известно, состоят из элементов L, R и С, а в некоторых случаях еще и из управляемых источников. Цифровые фильтры состоят из совсем других элементов, а именно:
a) элементов z-1, осуществляющих единичные задержки на один такт T (регистры сдвига для хранения предыдущих значений входных и выходных сигналов), обозначают их в соответствии с рисунком 21, a;
б) перемножителей, которые выполняют умножение или масштабирование – рисунок 21, б;
в) сумматоров, они же могут выполнять и вычитание – рисунок 21, в.
xk(n) xk-1(n) xk(n) A*xk(n) xk(n) xk(n)+уk(n)

z-1


уk(n)
а)
б)
в)
Рисунок 14 – обозначение элементов цифровых фильтров
Рассмотрим реализацию передаточной функции цифрового фильтра прямым методом [2]. Он основан на том, что передаточной функции
 , (46)
, (46)
соответствует разностное уравнение
![]() .
(47)
.
(47)
У равнению
(47) отвечает схема на рисунке 22.
равнению
(47) отвечает схема на рисунке 22.
Рисунок 15 – Схема реализации разностного уравнения
Таким образом, передаточная функция последовательного дискретного корректирующего устройства реализуется в виде:

Рисунок 16 – Схема последовательного дискретного корректирующего устройства
5.3. Сравнение Графиков переходных процессов
График отображающий переходные процессы до и после коррекции можно увидеть на рис. 17
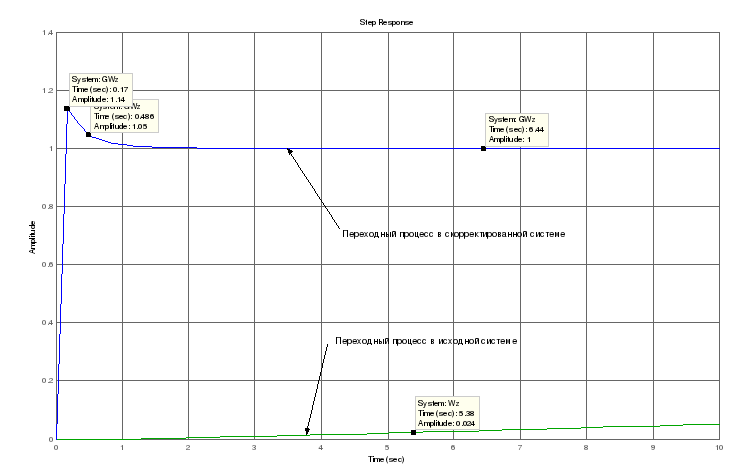
Рисунок 24 – Переходные процессы в замкнутой системе до и после коррекции
Из графика видно что после коррекции переходный процесс стал устойчивым, т.е. коррекция было проведена верно.
Заключение
В состав спроектированной САУ подъема шасси спортивного самолета следует включить последовательное дискретное корректирующее устройство (микроконтроллер), потому что оно обеспечивает хорошие динамические характеристики, и при этом лишено недостатков аналогового корректирующего устройства. Так как двукратное дифференцирование сигнала пассивными четырехполюсниками ведет к повышению уровня помех, а также изменение характеристик R, C элементов в результате действия внешних факторов или старения скажется на динамических свойствах корректирующего устройства. Микроконтроллер за счет свойств цифрового сигнала менее подвержен помехам, и изменение характеристик полупроводниковых элементов меньше скажется на качестве регулирования.
Кроме того, путем программирования микроконтроллера, можно изменять его передаточную функцию, в зависимости от требуемых характеристик. Например, уменьшить время переходного процесса, или увеличить запасы устойчивости.
