
- •Статистическая проверка гипотез.
- •2.1 Понятие о статистических гипотезах
- •2.2 Ошибки при проверке гипотез. Уровни статистической значимости
- •2.3 Статистические критерии
- •Подсчет критерия
- •Задача 5.1
- •Гипотезы:
- •§1. Статистическая и корреляционная зависимости.
- •§2. Форма и направление корреляционной связи: уравнение регрессии, линия регрессии. Линейная корреляция, коэффициенты регрессии
- •§3. Коэффициент корреляции.
- •§4. Понятие об однофакторном дисперсионном анализе.
2.2 Ошибки при проверке гипотез. Уровни статистической значимости
Статистическая проверка гипотез, основанная на экспериментальных, выборочных данных, неизбежно связана с риском (вероятностью) принять ложное решение. Ошибки, допускаемые при проверке гипотез можно разделить на два типа.
|
Отклонение гипотезы Н0, в то время как она верна |
-
ошибка 1-го рода.
Вероятность ошибки 1-го рода обозначается
|
|
Принятие гипотезы Н0, в то время как она неверна |
-
ошибка 2-го рода.
Вероятность ошибки 2-го рода обозначается
|
Поскольку исключить ошибки при принятии статистических гипотез невозможно, то необходимо минимизировать возможные последствия, т. е. принятие неверной статистической гипотезы. В большинстве случаев единственный путь минимизации ошибок заключается в увеличении объема выборки.
При обосновании статистического вывода следует решить вопрос, где же проходит линия между принятием и отвержением нулевой гипотезы. Так как в эксперименте имеются случайные влияния, эта граница не может быть проведена абсолютно точно. Она базируется на понятии уровня значимости.
Статистическая
значимость результата (p-уровень)
– количественная мера уверенности в
его «истинности». Более высокий p-уровень
соответствует более низкой надежности
(уровню доверия) результата:
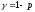 .
Величину
.
Величину
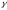 еще называют доверительной вероятностью.
Уровень значимости р представляет собой
вероятность ошибки, связанной с
распространением наблюдаемого результата
на генеральную совокупность.
еще называют доверительной вероятностью.
Уровень значимости р представляет собой
вероятность ошибки, связанной с
распространением наблюдаемого результата
на генеральную совокупность.
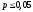 показывает, что имеет место 5% вероятность
того, что найденная в выборке связь
между переменными является лишь случайной
особенностью данной выборки. Таким
образом, уровень значимости – это
вероятность того, что мы сочли различия
существенными, а они на самом деле
случайны. Если мы указываем, что различия
достоверны на 1% уровне значимости (
показывает, что имеет место 5% вероятность
того, что найденная в выборке связь
между переменными является лишь случайной
особенностью данной выборки. Таким
образом, уровень значимости – это
вероятность того, что мы сочли различия
существенными, а они на самом деле
случайны. Если мы указываем, что различия
достоверны на 1% уровне значимости (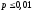 ),
то имеем в виду, что вероятность того,
что они все-таки недостоверны, составляет
0,01. В сущности уровень значимости р
представляет собой вероятность ошибки
1-го рода
),
то имеем в виду, что вероятность того,
что они все-таки недостоверны, составляет
0,01. В сущности уровень значимости р
представляет собой вероятность ошибки
1-го рода
 .
.
Любая гипотеза должна формулироваться, а уровень значимости задаваться исследователем всегда до получения экспериментальных данных, по которым эта гипотеза будет проверяться. При выборе уровня значимости исследователь исходит из практических соображений: какую вероятность ошибки он считает допустимой для его конкретной задачи.
Исторически сложилось, что в прикладных науках, использующих статистику, принято считать:
-
низшим уровнем статистической значимости 5%-ый уровень
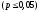 ;
; -
достаточным – 1%-ый уровень
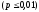 ;
; -
высшим - 0,1%-ый уровень
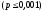 .
.
Поэтому в статистических таблицах критических значений обычно приводятся значения критериев, соответствующих данным уровням статистической значимости. Как видим, наибольшая величина, или нижняя граница, уровня статистической значимости равна 0,05 – это означает, что допускается пять ошибок в выборе из ста элементов (случаев испытуемых).
Для некоторых критериев указан точный уровень для различных эмпирических значений. Заметим также, что в современных статистических пакетах для компьютеров используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни могут иметь различное числовое выражение в интервале от 0 до 1.

 .
Вероятность же правильного решения:
.
Вероятность же правильного решения:
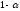 .
.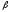 .
.