1. Анализ методов и принципов описания нелинейных электромеханических систем

1.1.1 Нелинейности в автоматических системах

Дифференциальные уравнения, описывающие динамику процессов в автоматических системах, могут быть нелинейными вследствие того, что в них некоторые переменные или их производные по времени входят не в первой степени или имеется произведение переменных и производных либо иная нелинейная комбинация. Кроме того, коэффициенты уравнений могут быть функциями переменных и их производных.

Нелинейные автоматические системы обычно представляют собой комплекс произвольного конечного числа звеньев, причем динамика большинства из них описывается линейными дифферен­циальными уравнениями, а одно или несколько звеньев описы­ваются нелинейными уравнениями.[1,3,8]

Как линейные, так и нелинейные системы при исследовании удобно представлять структурными схемами (математическими моделями). Для примера на рис. 1.1 представлена структурная схема нелинейной системы, в которой линейные звенья обозначены передаточными функциями с соответствующими индексами, а нелинейное звено представлено в виде некоторой нелинейной функции . На схеме через g обозначено задающее воздействие, через у – выходная величина системы, а через f₁ и f₂ — возмущающие воздействия, приложенные к системе.

Рисунок - 1.1 Структурная схема нелинейной системы

При рассмотрении нелинейных звеньев следует отличить понятие нелинейного звена от понятия нелинейности. Нелинейным звеном называется некоторый элемент системы, который описывается нелинейным уравнением, например

– безынерционное нелинейное звено (здесь х₁ и х₂ – входная и выходная величины нелинейного звена);

– инерционное нелинейное звено;

или уравнением

– нелинейное звено с временным запаздыванием.

Под знаком нелинейной функции может находиться как входная, так и выходная переменная нелинейного звена. Нелинейное звено может описываться уравнением, содержащим как линейные, так и нелинейные члены. Под нелинейностью понимается нелинейная функция, входящая в уравнение нелинейного звена.[4,7]

При применении некоторых методов исследования нелинейных систем, например метода гармонической линеаризации, удобно переходить к свернутым структурным схемам, выделяя нелинейное звено, а все линейные звенья объединяя в единый структурный блок, называемый линейной частью системы. Так, нелинейную систему со структурной схемой, изображенной на рис. 1.1, в свернутом виде можно представить, как показано на рис. 1.2, а.

Рисунок – 1.2 Структурная схема нелинейной системы

Линейная часть системы сама по себе может иметь любую структуру, в том числе многоконтурную, с различного вида корректирующими устройствами.

При этом, отнеся к линейной части линейное уравнение, получим приведенную линейную часть и нелинейность (рис. 1.2б). В нелинейных автоматических системах очень часто нелинейности приходится учитывать в виде статических характеристик (статические нелинейности). Эти характеристики могут быть однозначными нечетно-симметричными, двузначными гистерезисными, однозначными четно-симметричными, двузначными опере­жающими и в общем случае любыми несимметричными.

Рисунок – 1.3 Однозначные нечетно-симметричные нелинейности: а – идеальная релейная характеристика б – релейная характеристика с зоной нечувствительности в – характеристика с насыщением или ограничением, г – характеристика с переменным коэффициентом усиления.

Здесь и далее на статических характеристиках угол наклона соответст­вующего участка в целях экономии места обозначается условно через k вместо arctg k (k есть коэффициент усиления).[5,8,9,10]

Рисунок – 1.4 Некоторые гистерезисные двузначные статические характеристики: а – релейная характеристика общего вида, б – релейная гистерезисная характеристика в – характеристика для учета люфта или зазора

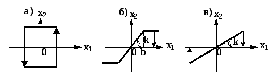
Рисунок – 1.5 Двузначные опережающие характеристики, а – в соответствуют специально создаваемым нелинейным корректирующим устройствам

Рисунок – 1.6 Несимметричные статические нелинейности а, б, в – четносимметричная нелинейная характеристика

Учет одной нелинейности в системе представляет более простую задачу расчета нелинейных автоматических систем. Часто приходится учитывать несколько существенных нелинейностей. Кроме статических, в дифференциальные уравнения могут вхо­дить нелинейности от производных переменных нелинейного звена – динамические нелинейности. [1,8,10]