
- •1. Мгновенная мощность
- •Анализ методов и принципов описания нелинейных электромеханических систем
- •1.1.1 Нелинейности в автоматических системах
- •Свойства и методы исследования нелинейных систем
- •2.Составляющие мощности на нелинейной индуктивности
- •2.1 Идентификации нелинейных параметров в асинхронном двигателе
- •Висновки
- •Перелік посилань
- •Секція «Електромеханічні системи з електроприводом змінного струму»
- •Дніпродзержинськ 2011
ДЕВІЗ: ” УЧЕНИЕ-СВЕТ! ”
Дослідження параметрів асинхронних двигунів з НЕЛІНІЙНІСТЮ в силовому контурі
АНОТАЦІЯ
Актуальність роботи. Літературний аналіз попередніх досліджень показав, що в ході довгострокової експлуатації і ремонту змінюються характеристики асинхронних двигунів (АД), що є наслідком зміни параметрів машин. На сьогоднішній день відсутні ефективні методи контролю і діагностичного устаткування, використання якого дозволить отримати повне уявлення про реальний розподіл енергії в електричній машині.
Отримання достовірної інформації про стан АД дасть можливість оцінити реальний розподіл енергії в машині і визначити максимально точне значення нелінійних параметрів АД при різних режимах роботи. При такому підході можлива розробка методики відбракування машин, що пройшли ремонт, на стадії післяремонтного випробування, а також методики післяремонтної паспортизації машин.
Мета роботи і задачі дослідження. Розробка способу для підвищення точності визначення електромагнітних параметрів АД.
Для досягнення цієї мети поставлені та вирішенні наступні задачі дослідження:
– розроблено математичний апарат для дослідження параметрів асинхронних двигунів з нелінійністю в силовому контурі;
– досліджено визначення нелінійності АД.
Об'єкт дослідження. Перехідні процеси в АД.
Предмет дослідження. Параметри АД.
Методи досліджень. При вирішенні поставлених задач використовувались загальні методи теорії електропривода, електротехніки та математичного моделювання.
Основні наукові та практичні результати, їх значення. Розроблено математичний апарат та досліджено параметрів асинхронних двигунів з нелінійністю в силовому контурі
Загальна характеристика наукової роботи. У роботі створено математичний апарат для дослідження параметрів асинхронних двигунів з нелінійністю в силовому контурі.
КЛЮЧОВІ СЛОВА. АСИНХРОННИЙ двигун, НЕЛІНІЙНІСТЬ.
ДОВІДКА
Про ступінь самостійності студентської роботи
Перед студентом була поставлена наукова задача розробити та дослідити параметри асинхронних двигунів з нелінійністю в силовому контурі.
Дана задача виконувалась у такій послідовності:
– розроблено математичний апарат для дослідження параметрів асинхронних двигунів з нелінійністю в силовому контурі;
– досліджено визначення нелінійності АД
ЗМІСТ
СЕКЦІЯ «Електромеханічні системи з електроприводом змінного струму» 1
1.1Анализ методов и принципов описания нелинейных электромеханических систем 12
2.Составляющие мощности на нелинейной индуктивности 17
Висновки 23
Перелік посилань 24
1. Мгновенная мощность
Аналіз енергопроцесів, що відображають поведінку електромеханічного комплексу, який включає електромеханічну систему і виробничий механізм з передавальним пристроєм, слід проводити з використанням рівнянь балансу потужностей або енергій. Ефективне застосування такого підходу можливо за наявності сукупності рівнянь для складових миттєвої потужності у всіх елементах електротехнічного комплексу. Базовим рівнянням балансу є рівність миттєвої потужності джерела живлення Pи(t) і сум миттєвих потужностей елементарних споживачів, що входять в комплекс:
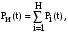
де
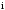 – індекс
відповідного елементарного споживача;
– індекс
відповідного елементарного споживача;
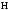 – кількість елементарних споживачів.
– кількість елементарних споживачів.
Баланс потужності витікає як наслідок з теореми Телледжена: сума творів напруги Ui та струмів Ii всіх гілок ланцюга, що задовольняють законам Кирхгофа, дорівнює нулю. Перемноживши UiIi – отримаємо миттєву потужність Pi i-й гілки, тому сума потужностей всіх гілок ланцюга дорівнює нулю. Якщо виділити гілки з незалежними джерелами, то баланс потужності можна сформулювати наступним чином: сума потужностей, що віддаються незалежними джерелами, дорівнює сумі потужностей, споживаних рештою гілок електричного ланцюга.
Стосовно
відомої Т-подібної схеми заміщення
асинхронного двигуна з індуктивностями
розсіювання статора
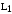 та
ротора
та
ротора
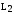 ,
індуктивністю контуру намагнічування
,
індуктивністю контуру намагнічування
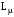 ,
опором статора
,
опором статора
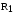 ,
опором
ротора
,
опором
ротора
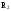 та опором
контуру намагнічування
та опором
контуру намагнічування
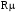 ,
в якості елементарних споживачів
виступає кожний з параметрів схеми
заміщення. Рівняння балансу миттєвої
потужності однієї фази двигуна складаються
у вигляді рівності складових миттєвої
потужності джерела живлення і складових
миттєвої потужності всіх елементів
електромеханічної системи:
,
в якості елементарних споживачів
виступає кожний з параметрів схеми
заміщення. Рівняння балансу миттєвої
потужності однієї фази двигуна складаються
у вигляді рівності складових миттєвої
потужності джерела живлення і складових
миттєвої потужності всіх елементів
електромеханічної системи:
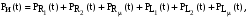
де
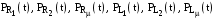 – значення миттєвих потужностей
елементів схеми заміщення:
– значення миттєвих потужностей
елементів схеми заміщення:
– для
активного опору
 ;
;
– для
індуктивності
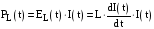 ;
;
– для
ємності
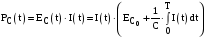 ;
;
– для нелінійного активного опору;
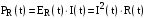 ;
;
– для нелінійної індуктивності
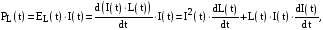
де
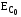 – залишкова
ЕРС.
– залишкова
ЕРС.
Використання цих залежностей для практичних цілей, наприклад, рішення ідентифікаційних задач або оцінки характеру енергетичного режиму, здійснюється шляхом представлення напруг і струмів в ланцюгах аналізованої схеми у вигляді гармонійних рядів. Це найпростіше реалізується за допомогою рядів Фур’є. При цьому з’являється можливість використовувати рівняння балансу косинусні і синусних складових всього ансамблю гармонік миттєвої потужності.
Представимо несинусоїдні залежності напруги і струму в формі усічених гармонійних рядів:
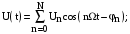
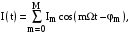
де
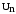 – амплітудні значення складових напруги
вищих гармонік;
– амплітудні значення складових напруги
вищих гармонік;
 – номер гармоніки
напруги;
– номер гармоніки
напруги;
 – число гармонік
напруги;
– число гармонік
напруги;
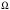 – кругова частота мережі;
– кругова частота мережі;
 – кут
здвигу
фаз між
напругою
та
речовій віссю «а» (
Приймаємо,
що вектор першої гармоніки напруги
співпадає
з речовою
віссю,
тобто
– кут
здвигу
фаз між
напругою
та
речовій віссю «а» (
Приймаємо,
що вектор першої гармоніки напруги
співпадає
з речовою
віссю,
тобто
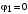 );
);
 – амплітудне
значення
складових
струма
вищих гармонік;
– амплітудне
значення
складових
струма
вищих гармонік;
 –
но–мер
гармоніки струму;
–
но–мер
гармоніки струму;
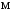 – число
гармонік струму;
– число
гармонік струму;
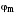 – кут
зрушення фаз між струмом і напругою .
– кут
зрушення фаз між струмом і напругою .
Використовуючи прості координатні перетворення з речовинною віссю «а» і уявної «b», одержимо:
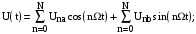
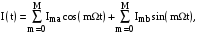
де

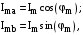
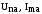 – косинусні
гармонійні складові напруги і струму;
– косинусні
гармонійні складові напруги і струму;
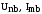 – синусні
гармонійні складові напруги і струму.
– синусні
гармонійні складові напруги і струму.
Тоді
залежність для миттєвої потужності
набуває вигляду: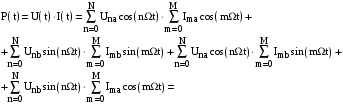
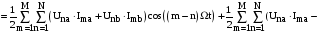
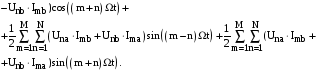
Із
залежності виходить, що миттєва потужність
складається з двох груп складових. Перша
група утворюється в результаті множення
одночастотних
компонент
напруги і струму, тобто при
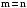 .
При
цьому частоти гармонік миттєвої
потужності рівні
.
При
цьому частоти гармонік миттєвої
потужності рівні
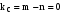 і
і
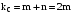 .
Нульова
частота
.
Нульова
частота
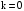 відповідає
постійному значенню потужності. .
відповідає
постійному значенню потужності. .
Друга
група складових миттєвої потужності
утворюється в результаті множення
різночастотних компонент напруги і
струму (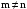 ).Частоти
гармонік миттєвої
потужності при цьому рівні
).Частоти
гармонік миттєвої
потужності при цьому рівні
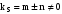 .
.
Для
зручності іменуємо частоти і складові
миттєвої потужності, одержані шляхом
перемножування одночастотних складових,
канонічними частотами і складовими і
відзначаємо індексом «с»
(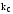 ,
,
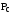 ),
а
відповідні частоти і складові миттєвої
потужності, одержані в результаті
перемножування різночастотних компонент,
- неканонічними і позначимо індексом
«s»
(
),
а
відповідні частоти і складові миттєвої
потужності, одержані в результаті
перемножування різночастотних компонент,
- неканонічними і позначимо індексом
«s»
(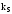 ,
,
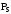 ).
Таким
чином, при
).
Таким
чином, при
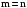 маємо
гармоніки потужності канонічного
порядку
маємо
гармоніки потужності канонічного
порядку
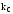 ,
а при
,
а при
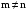 – неканонічного
порядку
– неканонічного
порядку
 .
.
Очевидно
також і те, що при певних значеннях m і
n може мати місце рівність
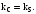 Це
означає, що сумарне значення гармонік
k-
порядку в загальному випадку повинне
визначатися у формі сум
k-х
складових
(канонічних і неканонічних):
Це
означає, що сумарне значення гармонік
k-
порядку в загальному випадку повинне
визначатися у формі сум
k-х
складових
(канонічних і неканонічних):
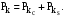
Розділення
знакозмінних складових потужності на
канонічні і неканонічні дозволяє
записати вираз для потужності у такому
вигляді: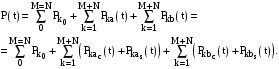
Гармоніки потужності (косинусниє і синусні) з частотами k виражаються так:
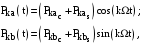
де
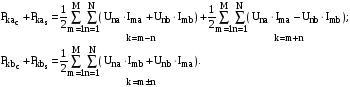
Значення
косинусних і синусних складових миттєвої
потужності в тих випадках, коли відомі
залежності
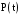 ,
можна
також визначити так:
,
можна
також визначити так:
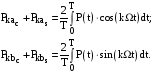
Таким
чином, миттєва потужність окрім постійної
компоненти включає косинусниє і синусні,
канонічні і неканонічні складові.
Частоти гармонік миттєвої потужності
(k) формуються в результаті множення
всього ансамблю гармонік напруги (n) і
струму (m) і визначаються так
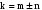 .
Так,
наприклад, 4-а
гармоніка миттєвої потужності
(
.
Так,
наприклад, 4-а
гармоніка миттєвої потужності
(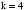 )за
наявності в сигналах напруги і струму
гармонік з номерами
)за
наявності в сигналах напруги і струму
гармонік з номерами
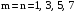 номерами
формується всіма даними гармоніками,
тобто
номерами
формується всіма даними гармоніками,
тобто
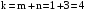 ;
;
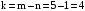 ;
;
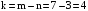 .
.
Картину
формирования гармоник мгновенной
мощности, ее канонических и неканонических
составляющих можно видеть из табл. 1.1.
Для примера примем гармоники напряжения
и тока с номерами
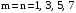 .
Постоянная составляющая формируется
из одночастотных составляющих напряжения
и тока
.
Постоянная составляющая формируется
из одночастотных составляющих напряжения
и тока
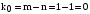 ;
;
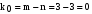 ;
;
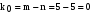 ;
;
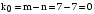 .
При перемножении одночастотных компонент
напряжения и тока формируются также
канонические составляющие мгновенной
мощности
.
При перемножении одночастотных компонент
напряжения и тока формируются также
канонические составляющие мгновенной
мощности
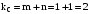 ;
;
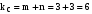 ;
;
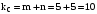 ;
;
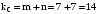 .
Умножение разночастотных компонентов
ведет к появлению неканонических
составляющих мгновенной мощности, т.е.
.
Умножение разночастотных компонентов
ведет к появлению неканонических
составляющих мгновенной мощности, т.е.
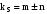 при
при
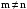 .
Полная мощность включает в себя сумму
как канонических, так и неканонических
составляющих
.
Полная мощность включает в себя сумму
как канонических, так и неканонических
составляющих
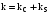 .
.
Выполненный
анализ указывает на возможность получения
зависимости, связывающей составляющие
тока и напряжения на конкретном элементе
схемы замещения с компонентами мгновенной
мощности
 -го
порядка. Это в свою очередь позволяет
составить уравнения баланса составляющих
гармоник мгновенной мощности на элементах
схемы замещения и источнике
полигармонического напряжения.
-го
порядка. Это в свою очередь позволяет
составить уравнения баланса составляющих
гармоник мгновенной мощности на элементах
схемы замещения и источнике
полигармонического напряжения.
Таблица 1.1 – Таблица гармоник напряжения, тока и составляющих мгновенной мощности
|
Анализируемые гармоники |
Гармоники |
||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
тока (m) |
- |
1 |
- |
3 |
- |
5 |
- |
7 |
- |
- |
- |
- |
- |
- |
- |
|
напряжения (n) |
- |
1 |
- |
3 |
- |
5 |
- |
7 |
- |
- |
- |
- |
- |
- |
- |
|
мгновенной мощности (k) |
0 |
- |
2 |
- |
4 |
- |
6 |
- |
8 |
- |
10 |
- |
12 |
- |
14 |
|
канонических составляющих мгновенной мощности (kс) |
0 |
- |
2 |
- |
- |
- |
6 |
- |
- |
- |
10 |
- |
- |
- |
14 |
|
неканонических составляющих мгновенной мощности (ks) |
- |
- |
2 |
- |
4 |
- |
6 |
- |
8 |
- |
10 |
- |
12 |
- |
- |
|
|
|||||||||||||||
Уравнения баланса мощности имеют общий характер и формируются в виде равенств составляющих мощности источника питания и составляющих мощности всех элементов электромеханической системы. В качестве составляющих мощности могут быть использованы активная мощность, реактивная мощность, канонические составляющие гармоник мгновенной мощности, неканонические составляющие гармоник мгновенной мощности, полные составляющие гармоник мгновенной мощности, которые включают канонические и неканонические составляющие. Уравнения баланса мощностей принимают вид:
– уравнения
баланса активной мощности
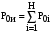 ;
;
– уравнения
баланса реактивной мощности
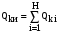 ;
;
– уравнения
баланса канонических составляющих
мгновенной мощности
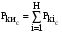 ;
;
– уравнения
баланса неканонических составляющих
мгновенной мощности
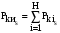 ;
;
– уравнения
баланса полных составляющих мгновенной
мощности
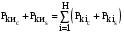 .
.
Как
показали исследования, достаточно
эффективные методы идентификации
параметров электромеханических систем
базируются на уравнениях баланса
мощности цепей схем замещения. Определение
электромагнитных параметров возможно
при питании асинхронного двигателя
полигармоническим напряжением. Схему
замещения асинхронного двигателя при
питании от тиристорного регулятора
напряжения можно представить Т-образной
схемой замещения, которая состоит из
первичного контура (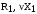 ),
контура намагничивания (
),
контура намагничивания (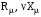 )
и вторичной цепи (
)
и вторичной цепи (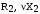 ).
).
Система уравнений баланса мощностей для Т-образной схемы замещения составляется для каждой из гармоник в виде равенства составляющих мгновенной мощности источника полигармонического напряжения сумме составляющих мгновенной мощности на активных и индуктивных сопротивлениях статорной и роторной цепей и контура намагничивания:
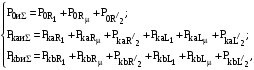
где
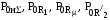 – постоянные составляющие мгновенной
мощности соответственно источника
полигармонического напряжения и активных
сопротивлений первичной цепи, контура
намагничивания и вторичной цепи;
– постоянные составляющие мгновенной
мощности соответственно источника
полигармонического напряжения и активных
сопротивлений первичной цепи, контура
намагничивания и вторичной цепи;
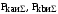 – косинусные и синусные составляющие
мгновенной мощности источника
полигармонического напряжения;
– косинусные и синусные составляющие
мгновенной мощности источника
полигармонического напряжения;
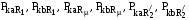 – косинусные и синусные составляющие
мгновенной мощности на активных
сопротивлениях первичной цепи, контура
намагничивания и вторичной цепи;
– косинусные и синусные составляющие
мгновенной мощности на активных
сопротивлениях первичной цепи, контура
намагничивания и вторичной цепи;
 – косинусные и синусные составляющие
мгновенной мощности на индуктивностях
первичной цепи, контура намагничивания
и вторичной цепи.
– косинусные и синусные составляющие
мгновенной мощности на индуктивностях
первичной цепи, контура намагничивания
и вторичной цепи.
Уравнения баланса
мощностей при использовании трех
гармоник напряжения и тока (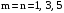 )
примут вид:
)
примут вид:

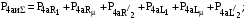
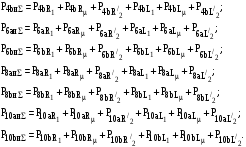
Анализ приведенных уравнений баланса гармоник мгновенной мощности показывает, что для определения электромагнитных параметров асинхронного двигателя с помощью Т-образной схемы замещения достаточно использовать три гармоники напряжения и тока, т.к. при этом получается 11 составляющих мгновенной мощности при 11 неизвестных схемы замещения (сопротивление статора R1 определяется заранее).
