6. Чисельне розв’язування задачі Коші для звичайних диференціальних рівнянь

Нехай маємо звичайне диференціальне рівняння 1-го порядку:

(13)

Треба знайти розв'язок цього рівняння, що задовольняє початковій умові

. (14)

При цьому будемо припускати, що функція задовольняє умовам теореми існування і єдиності розв'язку для звичайного диференціального рівняння 1-го порядку.

Знайти точний розв'язок задачі Коші (13, 14), тобто виразити його через елементарні або спеціальні функції, або подати його через квадратури від елементарних або спеціальних функцій вдається лише в небагатьох практичних задачах. Інколи, якщо навіть і вдається знайти точний розв'язок, він має досить складний вигляд і користуватися ним практично неможливо. Тому для розв’язування задачі Коші доводиться застосовувати наближені методи.

При чисельному інтегруванні диференціального рівняння (13) знаходять наближені значення (а інколи й точні) шуканого розв’язку в деяких фіксованих точках (вузлах) з відрізку . Припустимо, що вузли рівновіддалені, тобто , , – крок.

В кожній точці , , визначають відповідні значення розв'язку рівняння . Таким чином виходить таблиця:

			......
			......

1) Метод Ейлера

Найпростішим чисельним методом розв’язування задачі Коші (13, 14) є метод Ейлера, який відноситься до явних однокрокових методів.

Розглянемо рівняння (13) в околах вузлів , і замінимо в лівій частині похідну різницею , а в правій частині візьмемо значення функції у вузлах. Отримаємо апроксимацію рівняння (13)

. (15)

Оскільки вузли рівновіддалені, то з рівності (15) одержуємо

, (16)

Формула (16) є розрахунковою формулою методу Ейлера. Формула (16) являє собою грубе наближення розв'язку рівняння (13) за допомогою розкладу функції в ряд Тейлора в околі точки з відкиданням членів другого і більш високих порядків. Іншими словами, приріст функції покладається рівним її диференціалу.

Покладаючи , за допомогою формули (16) знаходимо значення функції при :

.

Значення задане початковою умовою (14).

Аналогічно знаходяться значення функції в інших вузлах:

;

……………………….

;

……………………….

2) Метод Рунге-Кутти

Метод Ейлера є окремим випадком методів, які відносяться до класу методів Рунне-Кутти. Ці методи використовують для обчислення значення , , попереднє значення , а також значення функції при деяких спеціальних чином обраних значеннях і .

Найбільш поширеним на практиці є метод Рунге-Кутти четвертого порядку точності. Обчислення проводяться за наступними формулами:

, (17)

де ;

;

;

;

.

Для контролю й оцінки точності обчислень обчислюють значення з кроком , значення з кроком і знаходять абсолютну похибку за формулою:

.

Обчислення зручно оформлювати у вигляді таблиці:

0
1
			.........	......
			.........	............
		........	.........	......
	........	........	.........	......

Приклад 4. Чисельно розв’язати задачу Коші для звичайного диференціального рівняння 1-го порядку

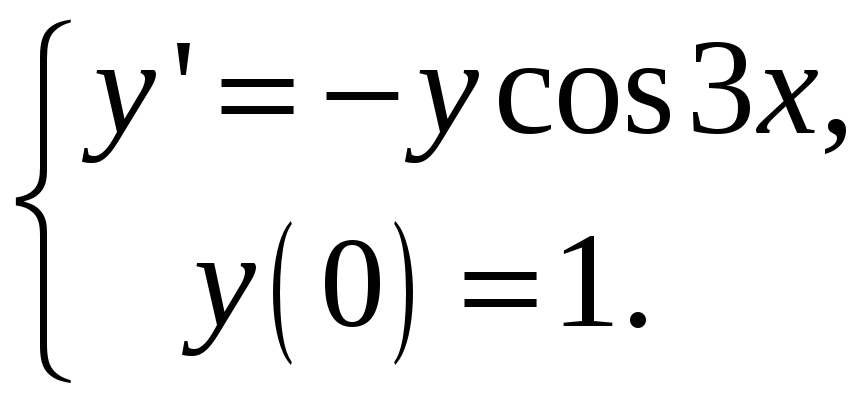
на відрізку із кроком .

а) методом Эйлера; б) методом Рунге-Кутти 4-го порядку.

Знайти точний розв’язок задачі. Побудувати на одному кресленні графіки точного й наближеного розв’язків.

Розв’язання. Знайдемо аналітичний розв’язок даного рівняння. Для цього відокремимо змінні:

, , .

Загальний розв’язок даного рівняння має вигляд:

,

де і –довільні сталі, які пов’язані між собою очевидним співвідношенням .

Щоб знайти частинний розв’язок, скористаємося початковими умовами, підставивши їх у загальний розв’язок:

.

Звідси . Остаточно, частинний розв’язок даного диференціального рівняння має вигляд:

. (18)

Отриманий аналітичний розв’язок даного диференціального рівняння буде використано як точний (еталонний) для порівняння з ним результатів наближених чисельних розв’язків методами Рунге-Кутти.

За умовою крок інтегрування . При цьому значенні інтегрування на всьому відрізку буде здійснено за кроків.

Послідовність дій на кожному кроці інтегрування в методах чисельного інтегрування Рунге-Кутти є однотипною, проте структура і складність виконуваних дій визначається порядком точності обраного методу.

а) У методі Ейлера (методі Рунге-Кутти першого порядку точності) на кожному кроці обчислення проводяться за формулами

, (16)

Послідовність розрахунків приведемо в таблиці, в якій крім результатів чисельного інтегрування представимо з метою порівняння також результати розрахунків за формулою (18).

		(за методом Ейлера)	(аналітичний розв’язок)
0	0	1,000	1,000
1	0,200	0,800	0,828
2	0,400	0,668	0,733
3	0,600	0,620	0,723
4	0,800	0,648	0,798
5	1,000	0,743	0,954
6	1,200	0,890	1,159
7	1,400	1,050	1,337
8	1,600	1,153	1,394
9	1,800	1,133	1,294
10	2,000	0,989	1,098

б) Послідовність розрахунків за формулами (17) оформимо у вигляді таблиці:

						(за методом Рунге-Кутти)
0	0	–	–	–	–	1,000
1	0,200	–0,200	–0,172	–0,185	–0,136	0,828
2	0,400	–0,137	–0,094	–0,097	–0,053	0,733
3	0,600	–0,053	–0,010	–0,010	0,033	0,723
4	0,800	0,033	0,075	0,077	0,118	0,798
5	1,000	0,118	0,155	0,158	0,189	0,954
6	1,200	0,189	0,207	0,209	0,209	1,159
7	1,400	0,208	0,183	0,182	0,131	1,337
8	1,600	0,131	0,059	0,058	–0,024	1,394
9	1,800	–0,024	–0,104	–0,101	–0,164	1,294
10	2,000	–0,164	–0,202	–0,199	–0,210	1,098