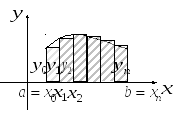
1) Формули прямокутників

Вважатимемо, що вузли розміщено так, що , , , . Крок в даному випадку дорівнює .

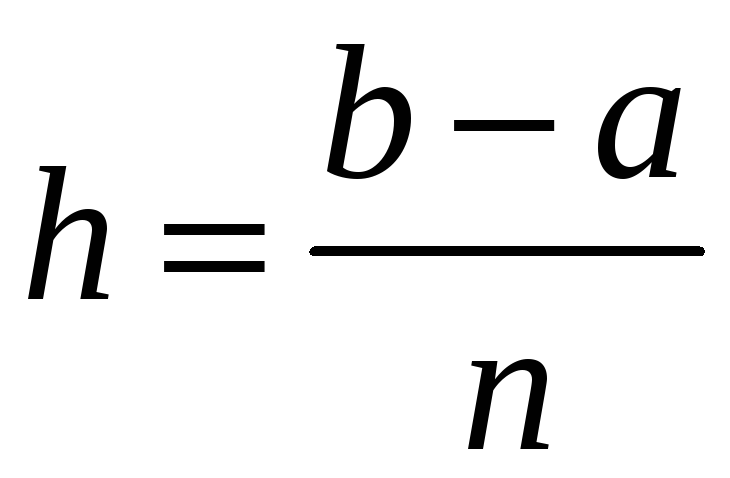Позначимо , , – значення даної функції у вузлах.

Замінимо задану криволінійну трапецію ступінчастою фігурою, що складається з прямокутників. Основи цих прямокутників однакові і дорівнюють 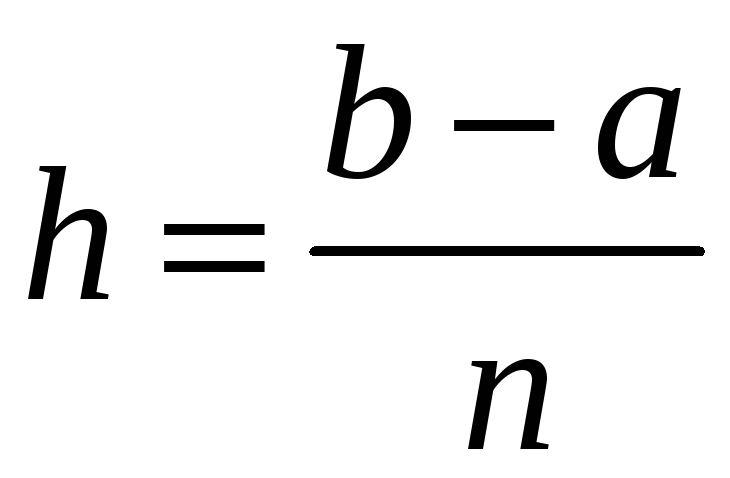, а висоти збігаються із значеннями в лівих або правих точках частинних інтервалів.

Для цих двох випадків отримуємо наступні формули прямокутників:

;

.

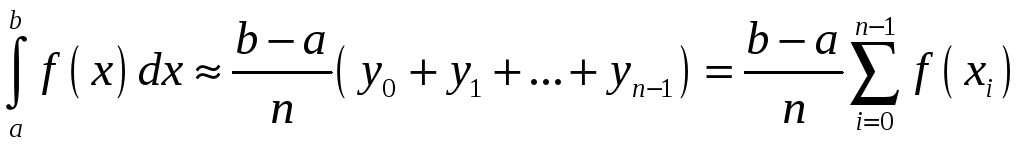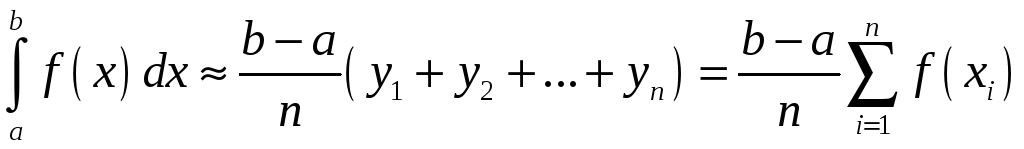які називаються формулами лівих і правих прямокутників відповідно.

Широко розповсюдженим і більш точним є вигляд формули прямокутників, який використовує значення функції в середніх точках елементарних відрізків . Тоді отримуємо формулу прямокутників:

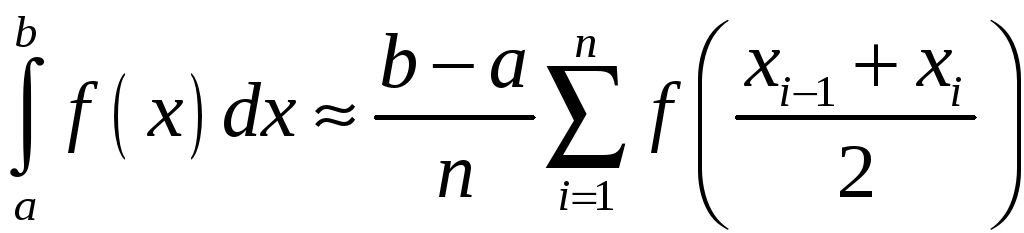. (10)

яка називається формулою середніх прямокутників.

2) Формула трапецій

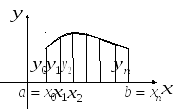
Замінимо криву не ступінчастою лінією, як у попередньому випадку, а ламаною, сполучивши сусідні точки . Тоді площа криволінійної трапеції наближено дорівнює сумі площ прямокутних трапецій, обмежених зверху відрізками цієї ламаної. Площа -ї частинної прямокутної трапеції дорівнює 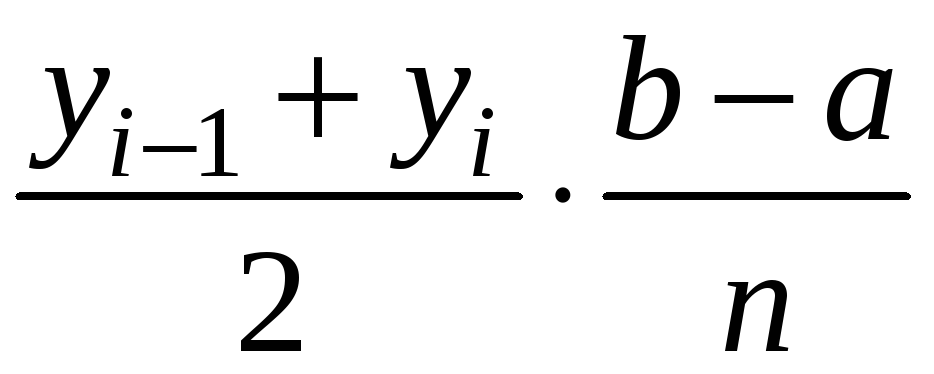, де і – основи -ї трапеції, а – її висота. Тому:

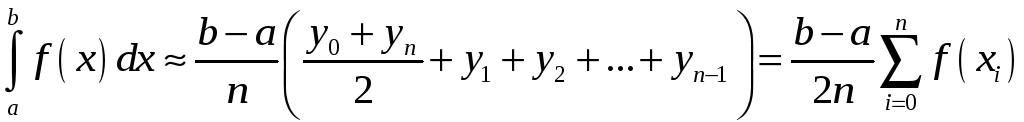. (11)

Формула (11) називається формулою трапецій.

3) Формула Сімпсона (формула парабол)

Розіб'ємо відрізок інтегрування на парне число () рівних частин з кроком . На кожному відрізку , , …, ,…, підінтегральну функцію замінимо інтерполяційним многочленом другого степеня:

, .

За можна взяти інтерполяційний многочлен Лагранжа другого степеня, який проходить через точки , , :

.

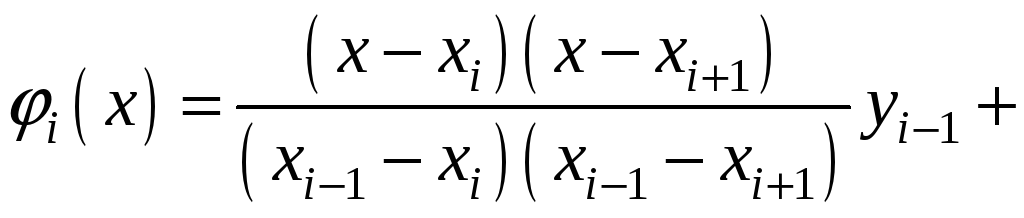
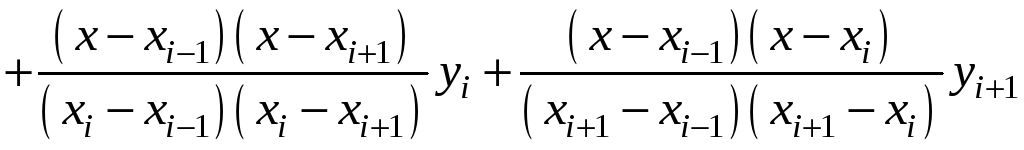Площа криволінійної трапеції, обмеженої параболою, яка проходить через точки , , , може бути обчислена за допомогою визначеного інтегралу:

.

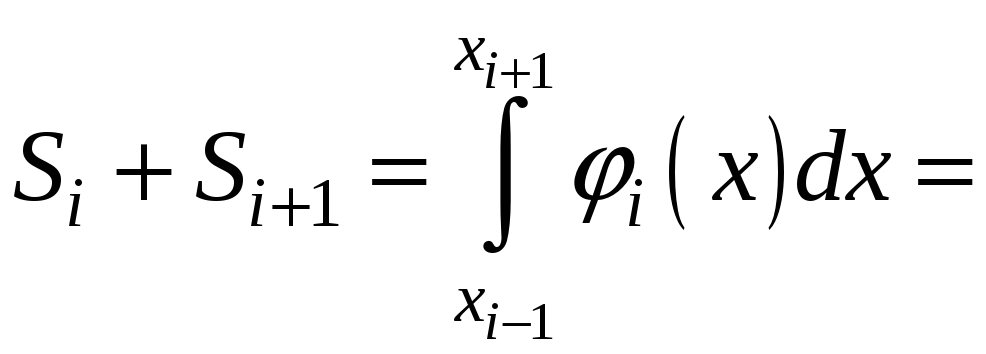
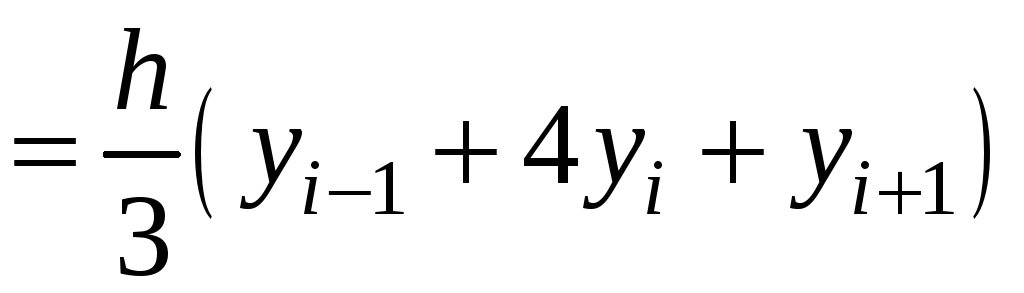Провівши такі обчислення для кожного елементарного відрізку , візьмемо суму отриманих виразів:

.

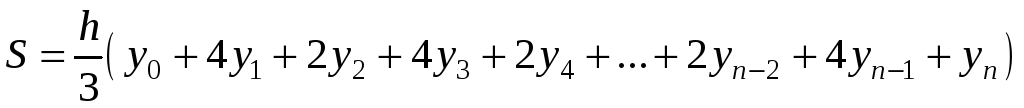Даний вираз для і приймається як значення визначеного інтеграла:

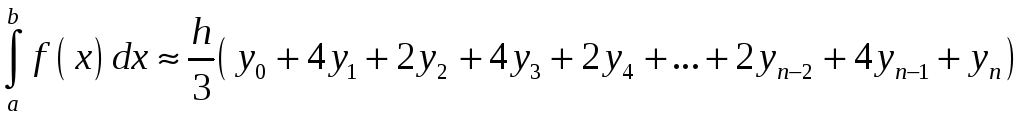. (12)

Формула (12) називається формулою Сімпсона або формулою парабол.

5. Похибки квадратурних формул

Різницю між лівою і правою частиною квадратурної формули

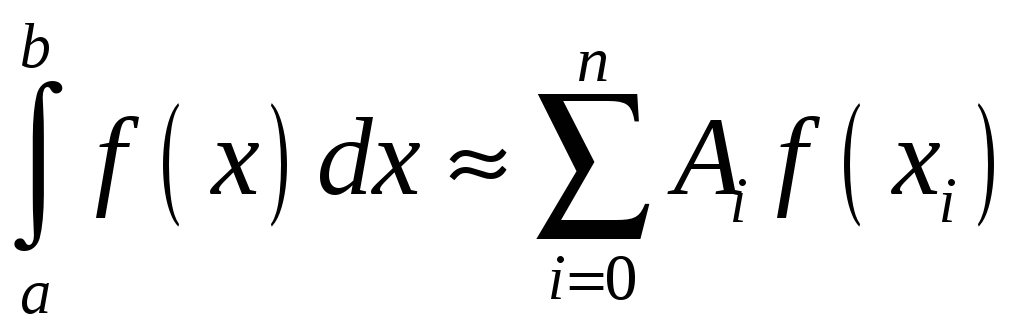, (8)

називають її залишковим членом і позначають :

.

Абсолютна похибка квадратурної формули, очевидно, залежить від числа частинних відрізків, на які розбивається відрізок інтегрування . Наступні формули дозволяють оцінювати абсолютні похибки квадратурних формул при відомому числі .

Якщо функція має на відрізку неперервну похідну і для будь-якого , то абсолютна похибка наближених формул (10), (11), (12) оцінюється формулою:

.

Якщо функція має на відрізку неперервну другу похідну і для будь-якого , то абсолютна похибка формули прямокутників оцінюється формулою:

;

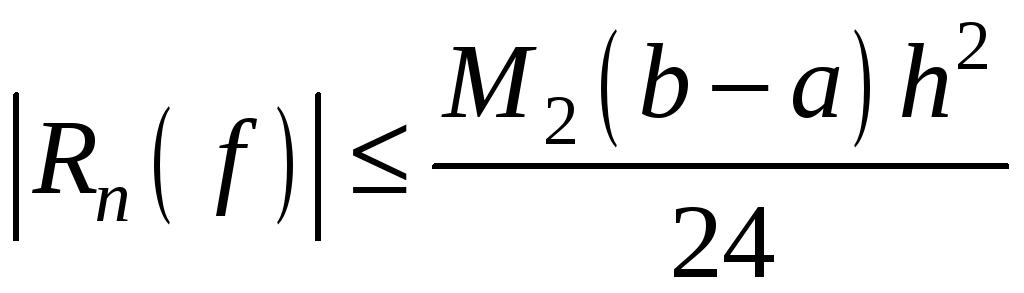формули прямокутників трапецій:

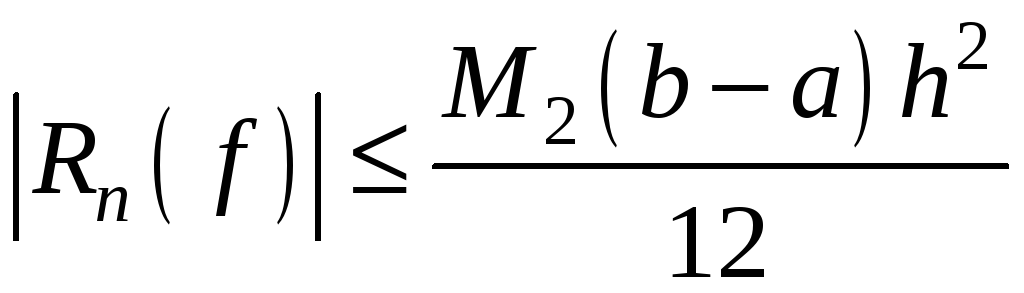
Абсолютна похибка квадратурної формули Сімпсона оцінюється формулою:

.

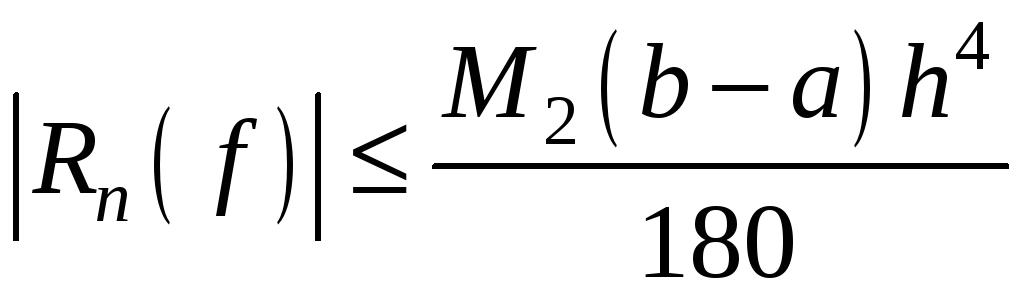Якщо функція має на відрізку неперервну четверту похідну і для будь-якого , то абсолютна похибка формули Сімпсона оцінюється формулою:

.

Можна вказати ще один практично зручний спосіб підрахунку помилки квадратурної формули Сімпосона. Якщо вважати, що міняється поволі, то отримуємо наближений вираз для шуканої помилки :

Хай і наближені значення інтеграла з кроком h і кроком 2h. Тоді:

,

тобто 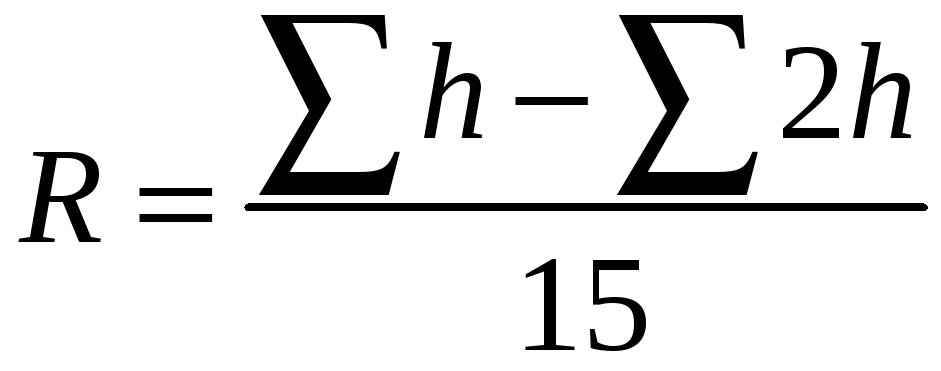(число частинних відрізків кратно 4).

Приклад 3. Обчислити інтеграл за квадратурною формулою:

а) прямокутників;

б) трапецій;

в) Сімпсона.

Оцінити похибку результатів.

Розв’язання. Точне значення інтеграла .

Розіб’ємо відрізок інтегрування на десять рівних частин: , . Обчислимо значення підінтегральної функції в точках розбиття , а також в середніх точках :

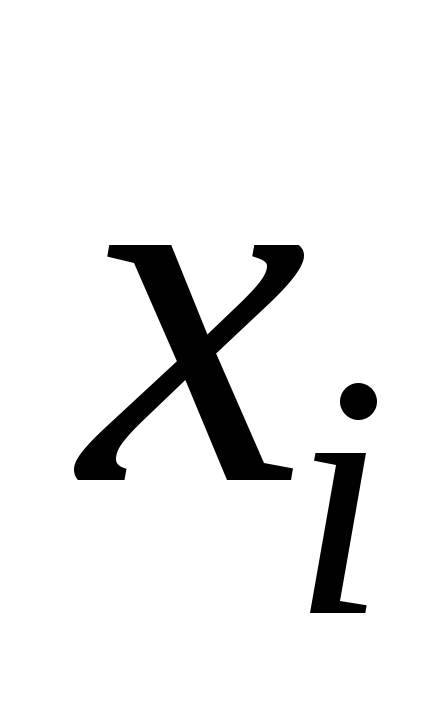
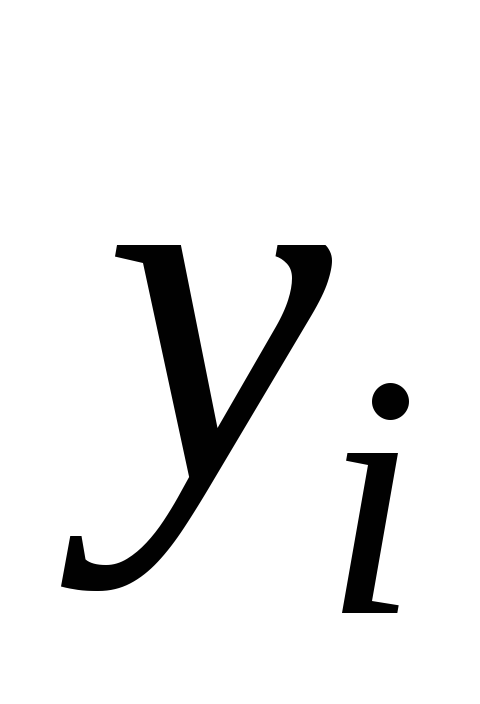
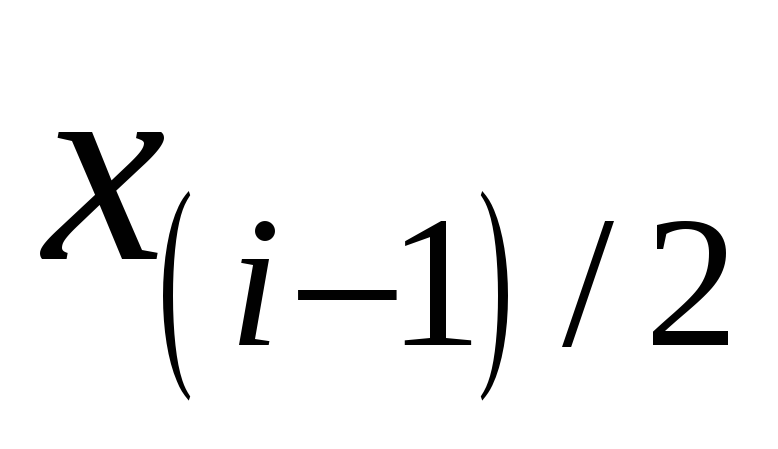
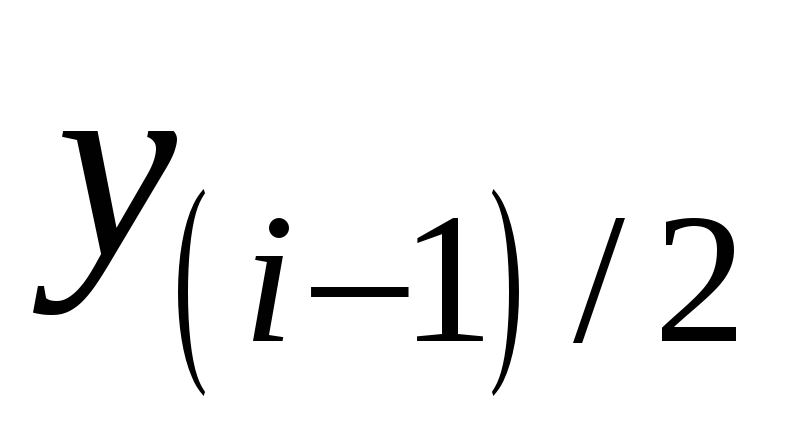
0	0,0	1,00000
1	0,1	0,90909	0,05	0,95238
2	0,2	0,83333	0,15	0,86957
3	0,3	0,76923	0,25	0,80000
4	0,4	0,71429	0,35	0,74074
5	0,5	0,66667	0,45	0,68966
6	0,6	0,62500	0,55	0,64516
7	0,7	0,58824	0,65	0,60606
8	0,8	0,55556	0,75	0,57143
9	0,9	0,52632	0,85	0,54054
10	1,0	0,50000	0,95	0,51282

а) Обчислимо інтеграл за формулою прямокутників (10):

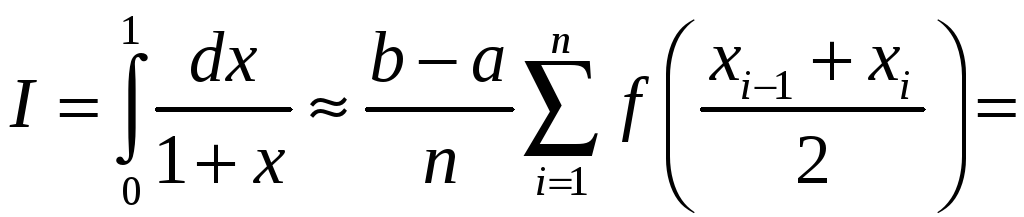
Оцінимо похибку результату. У даному випадку ,

.

.

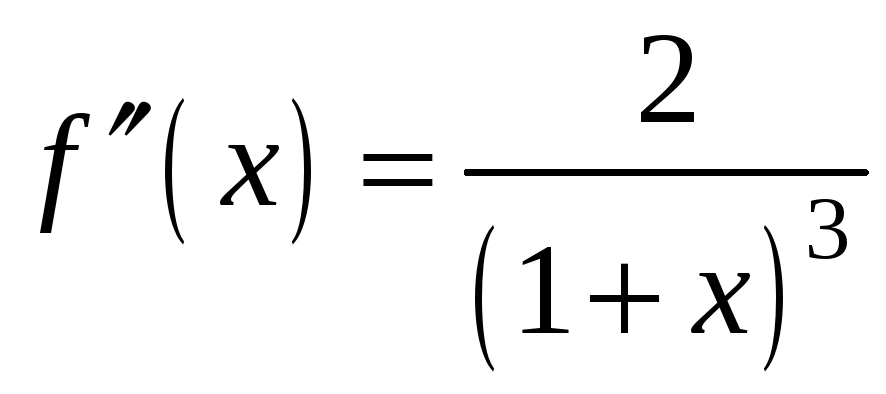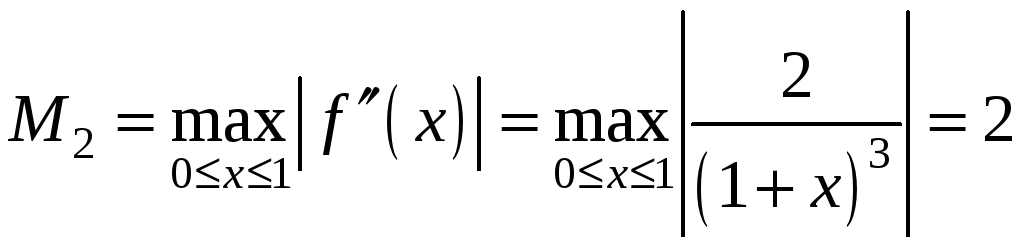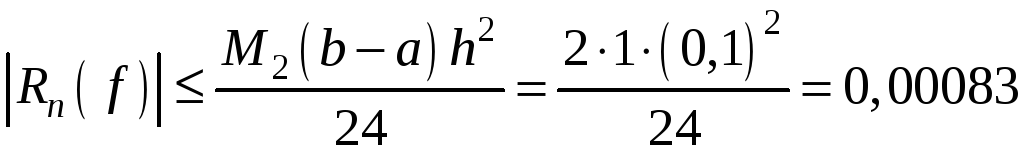Отже, добутий результат потрібно записати так: (залишаємо дві правильні цифри і одну сумнівну): .

а) Обчислимо інтеграл за формулою трапецій (11):

.

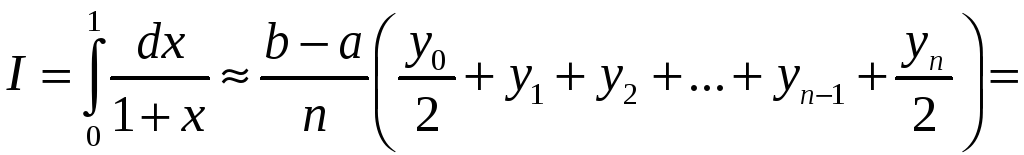
Оцінимо похибку результату. У даному випадку ,

.

.

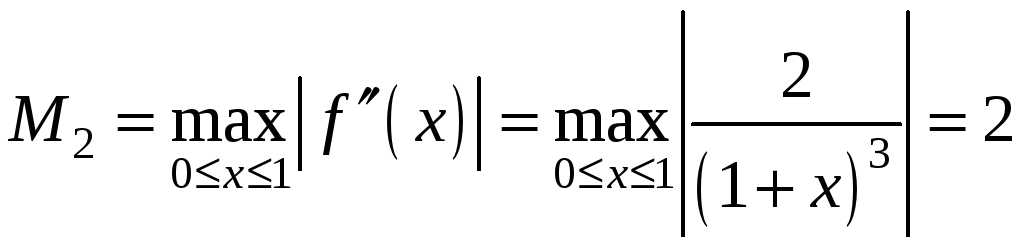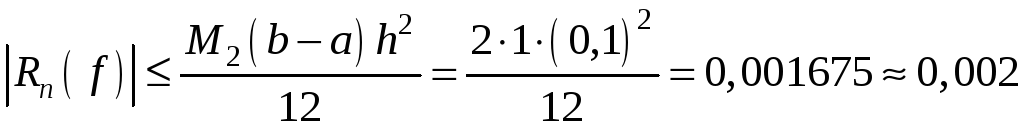Отже, добутий результат потрібно записати так: .

а) Обчислимо інтеграл за формулою Сімпсона (12):

.

.

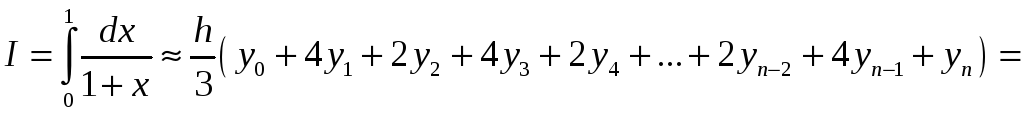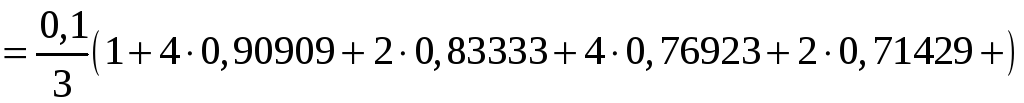
Оцінимо похибку результату. У даному випадку ,

.

.

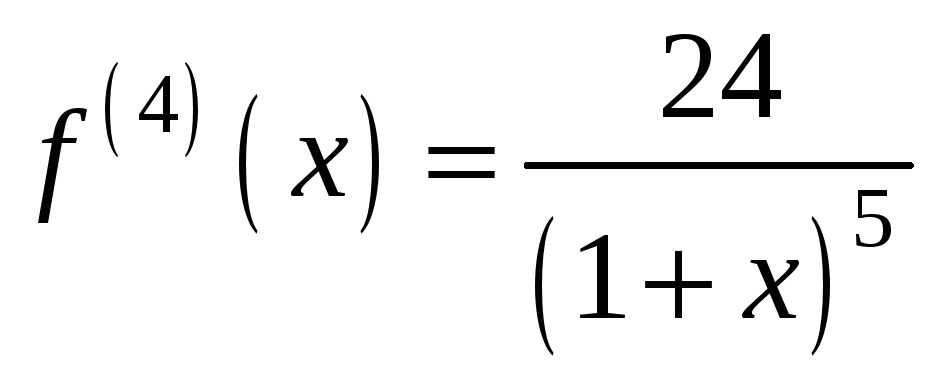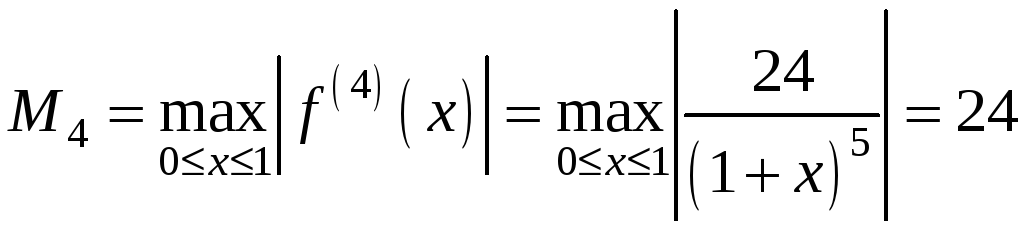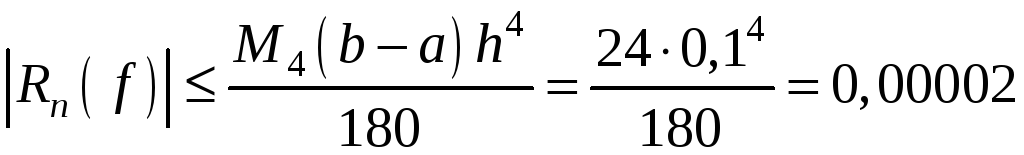Отже, в отриманому результаті не менш як чотири значущі цифри правильні. Порівнявши цей результат з точним значенням інтеграла, переконаємося, що в ньому правильні всі п’ять значущих цифр. Отже, добутий результат потрібно записати так: .

Відзначимо, що формула Сімпсона значно точніша формули прямокутників і формули трапецій.