Тема 6 Чисельне диференціювання й інтегрування

1. Наближення похідних

Нагадаємо, що похідною функції називається границя відношення приросту функції до приросту аргументу при прямуванні до нуля:

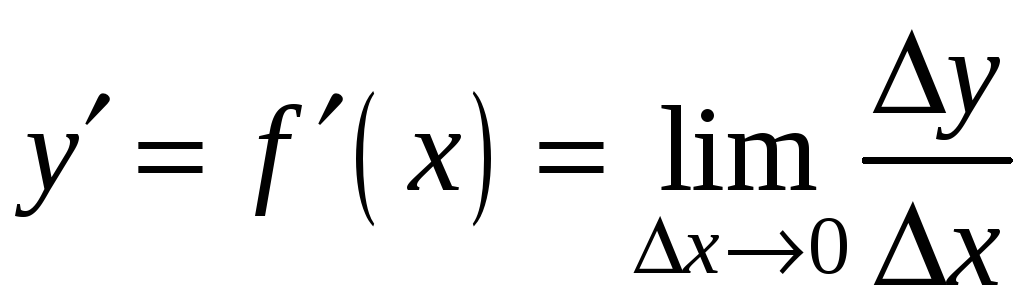, . (1)

Звичайно для обчислення похідних використовують готові формули (таблицю похідних) і до виразу (1) не вдаються. Але в чисельних розрахунках за допомогою комп’ютера використання формул з таблиці похідних не завжди зручно і можливо. Наприклад, якщо заданий явний вид функції, то вираз для похідної часто виявляється достатньо складним і бажано його замінити простішим. Якщо ж функція задана тільки своїми значеннями в деяких точках з відрізку (таблично), то одержати явний вид її похідних взагалі неможливо. У цих ситуаціях виникає необхідність наближеного (чисельного) диференціювання.

Проста ідея чисельного диференціювання полягає в тому, що функція на розглядуваному проміжку замінюється інтерполяційним многочленом і похідна функції наближено замінюється відповідною похідною інтерполяційного многочлена:

, . (2)

Аналогічно знаходять похідні вищих порядків:

, .

Залежно від форми інтерполяційного многочлена для функції , похідну від якої треба знайти, дістаємо різні формули чисельного диференціювання відповідно до наближеної рівності (2).

Нехай функція задана своїми значеннями в різних точках з відрізку , які позначимо , . Припустимо, що вузли рівновіддалені, тобто , , – крок. В цьому випадку функція може бути апроксимована інтерполяційним многочленом Ньютона:

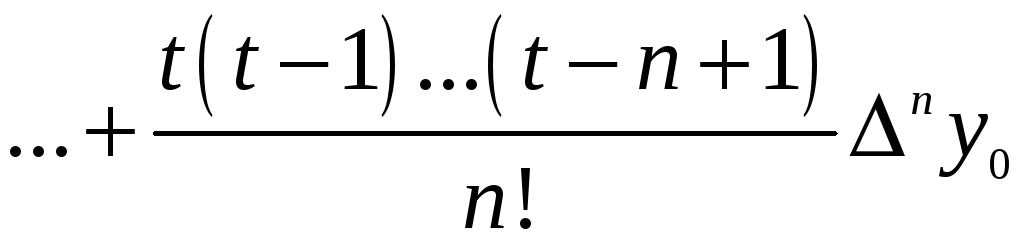, де .

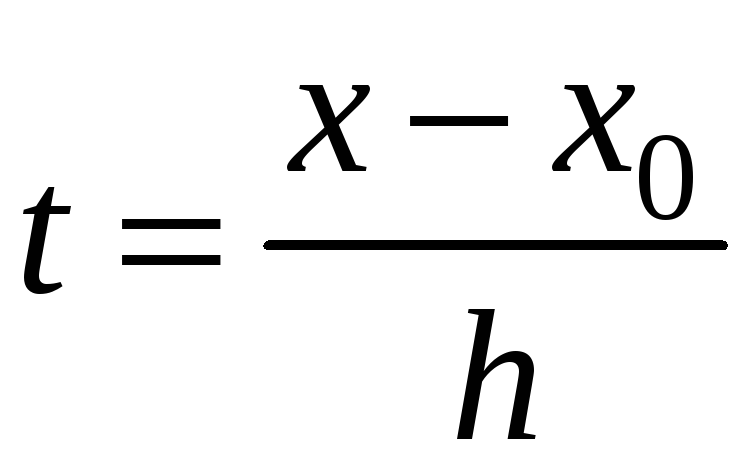Вважатимемо, що похідна від функції у будь-якій точці наближено дорівнює похідній від многочлена . Щоб знайти похідну многочлена , подамо його в іншому вигляді, а саме: запишемо за степенями кожний доданок.

Відомо, що

, (3)

де через позначено суму всіх можливих добутків натуральних чисел від 1 до по множників. Наприклад, при матимемо:

.

На основі (3) многочлен запишемо так:

.

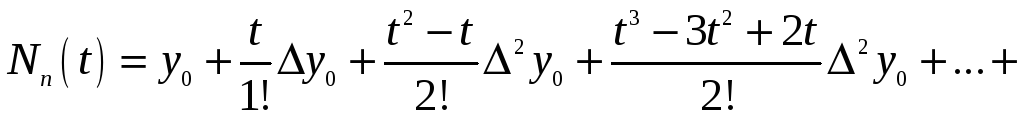
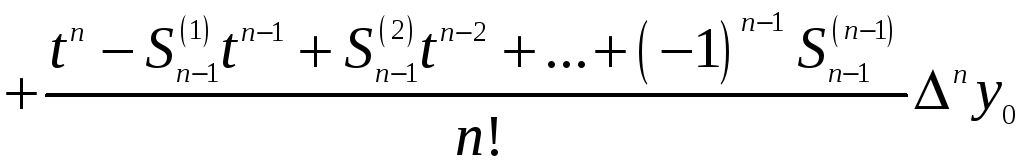Диференціюючи цей многочлен по змінній з урахуванням правила диференціювання складеної функції:

,

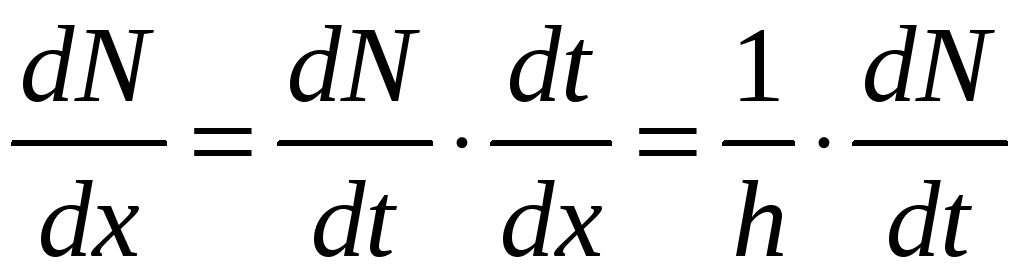отримуємо формулу для обчислення похідної:

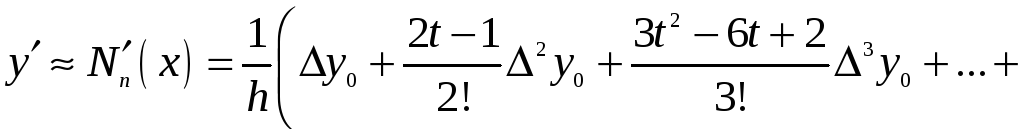
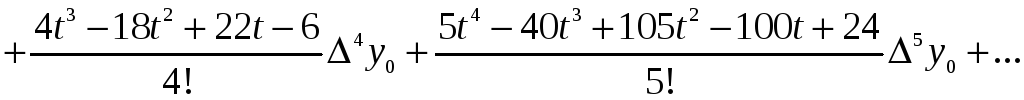
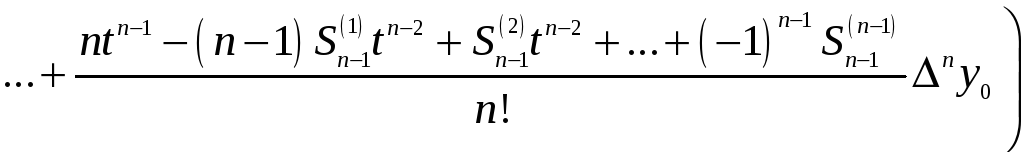(4)

Рівність (4) – шукана формула чисельного диференціювання.

Вона значно спрощується для знаходження похідної в табличних точках . Наприклад, якщо , дістанемо такі формули:

,

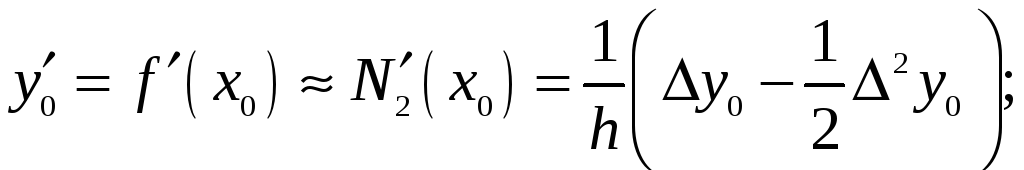
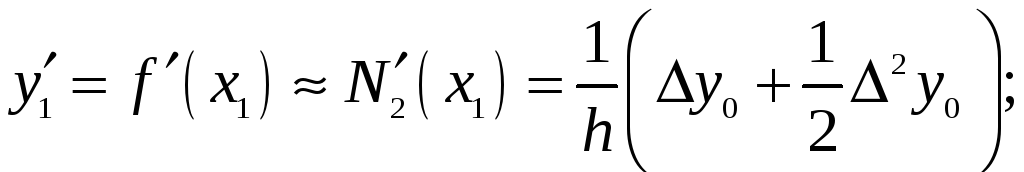
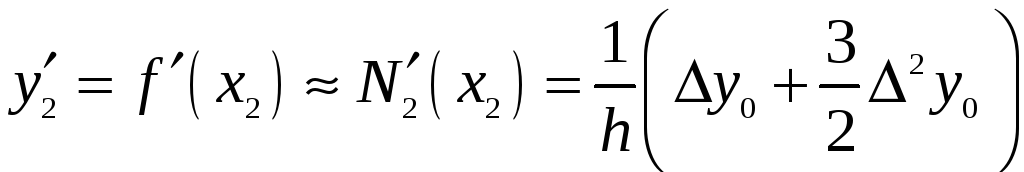або врахувавши вирази для скінченних різниць, подані через значення функції:

.

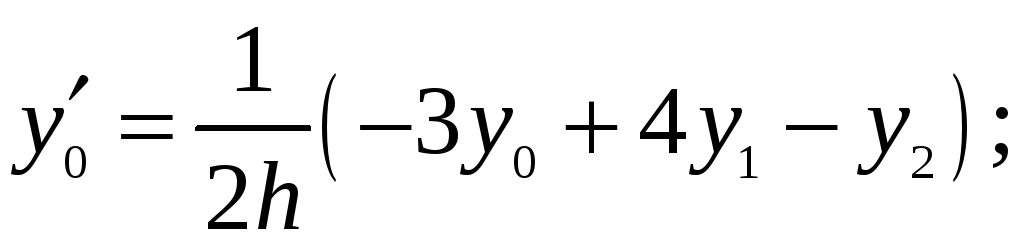
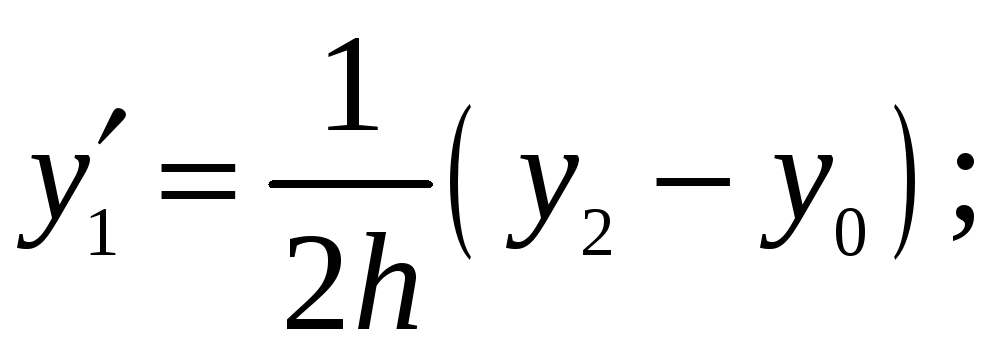
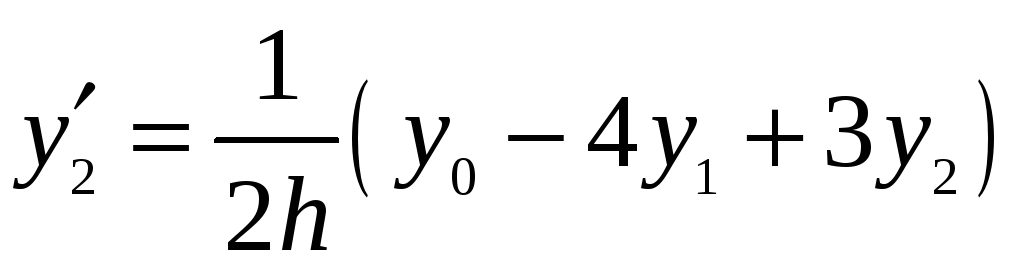Якщо в таблиці функції задано її значення в достатній кількості вузлів, то, очевидно, кожне табличне значення можна вважати за початкове. Так, якщо , то формула (4) набере вигляду:

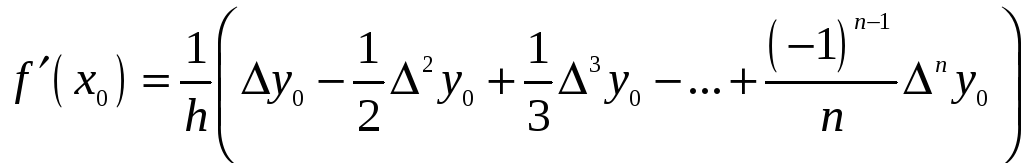(5)

З формули (4) можна отримати формулу для обчислення похідних будь-якого порядку:

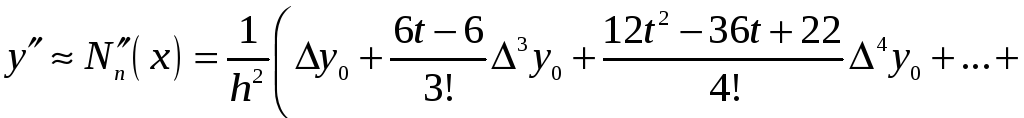
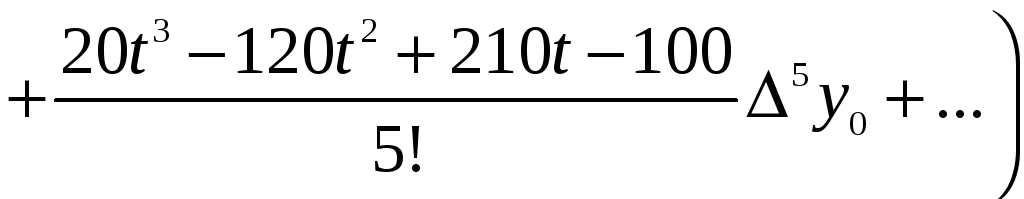(6)

……………………………………………………………………………..

Кількість доданків в цих формулах залежить від кількості вузлів, які використовуються для обчислення похідної.

Приклад 1. Обчислити в точці першу і другу похідні функції, заданої таблицею:

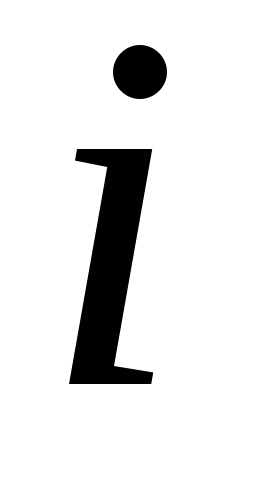
	0	1	2	3	4	5
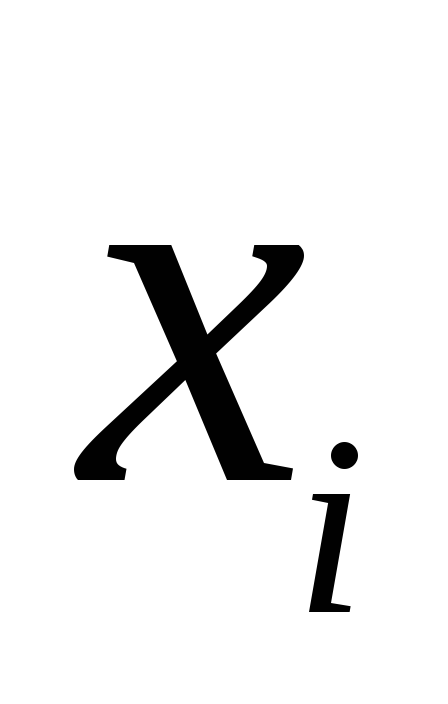
	0	0,1	0,2	0,3	0,4	0,5
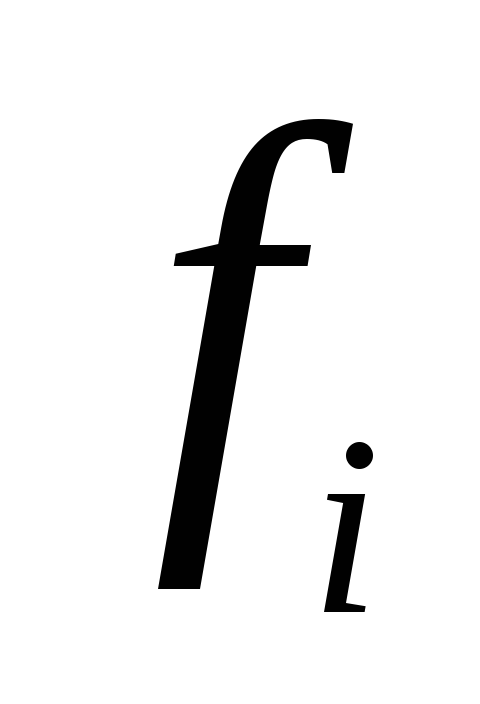
	1,2833	1,8107	2,3606	2,9577	3,5969	4,2833

Розв’язання. Побудуємо таблицю, в якій обчислимо скінченні різниці:

0	1,2833
		0,5274
0,1	1,8107		0,0325
		0,5599		0,0047
0,2	2,3606		0,0372		0,0002
		0,5971		0,0049		0,0000
0,3	2,9577		0,0421		0,0002
		0,6392		0,0051
0,4	3,5969		0,0472
		0,6864
0,5	4,2833

Оскільки четверті різниці практично сталі, покладемо . За умовою , 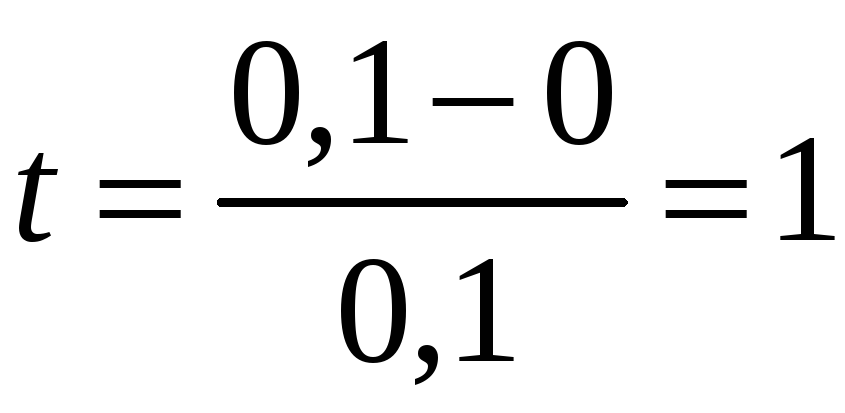. За формулою (4) одержимо:

.

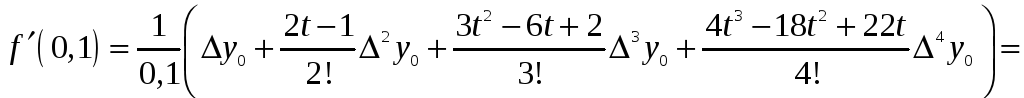
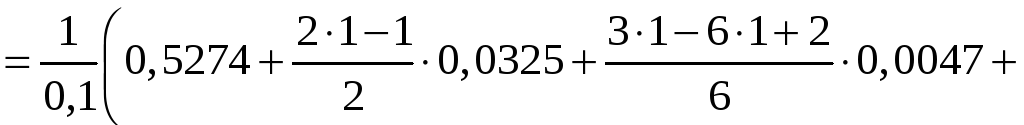
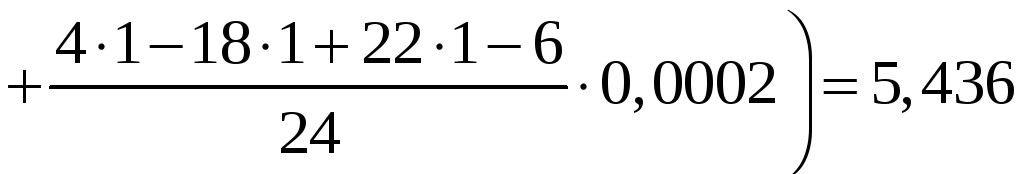За формулою (6) одержимо:

.

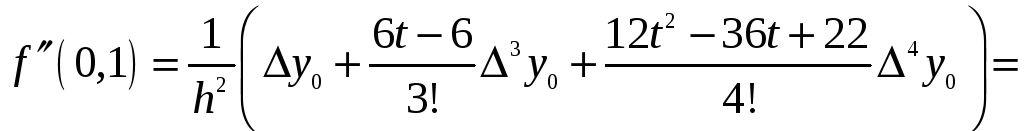
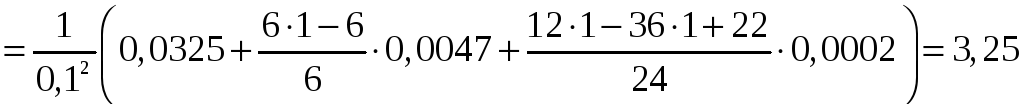Інтерполяційний многочлен Ньютона дає вирази для похідних через скінченні різниці , . На практиці часто вигідніше виражати значення похідних не через скінченні різниці, а безпосередньо через значення функції у вузлах. для отримання таких формул зручно скористатися інтерполяційним многочленом Лагранжа з рівновіддаленими вузлами , тобто , , – крок.

Запишемо інтерполяційній многочлен Лагранжа і його залишковий член для випадку трьох вузлів інтерполяції ():

.

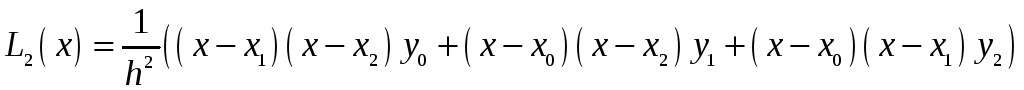
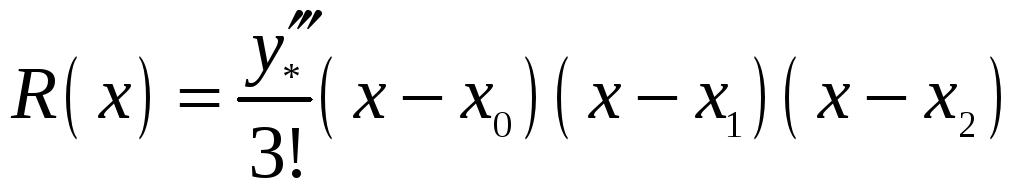Диференціюючи ці многочлени по змінній , отримаємо наступні апроксимації похідних при , , :

,

;

,

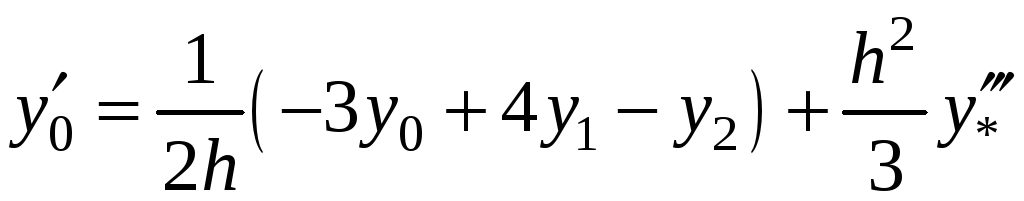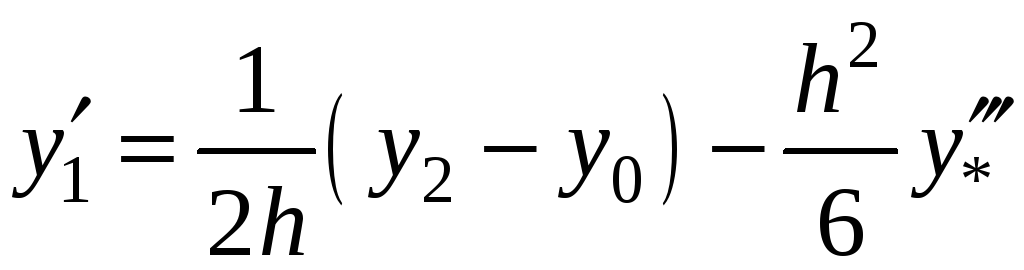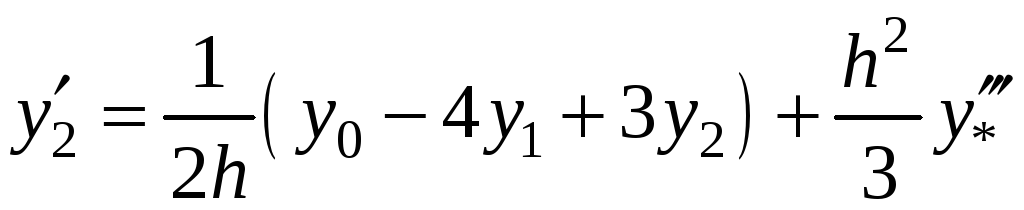де – значення похідної третього порядку в деякій внутрішній точці .

Записуючи інтерполяційній многочлен Лагранжа і його залишковий член для випадку чотирьох вузлів інтерполяції (), отримаємо наступні апроксимації похідних при , , , :

;

;

;

.

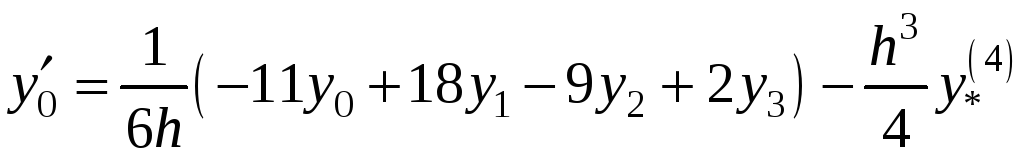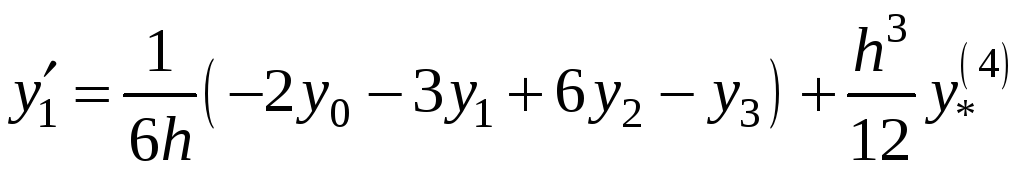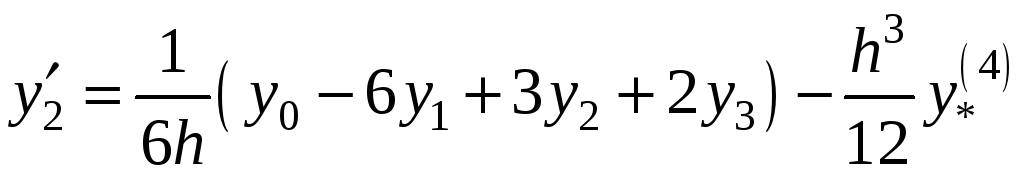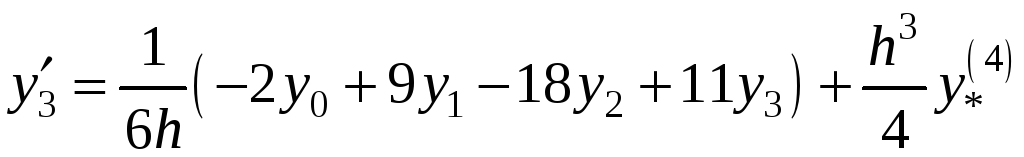Приклад 2. Обчислити в точці першу похідну функції, заданої таблицею:

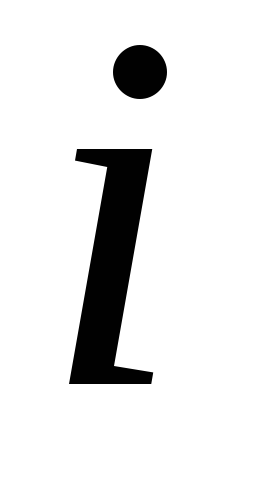
	0	1	2	3	4	5
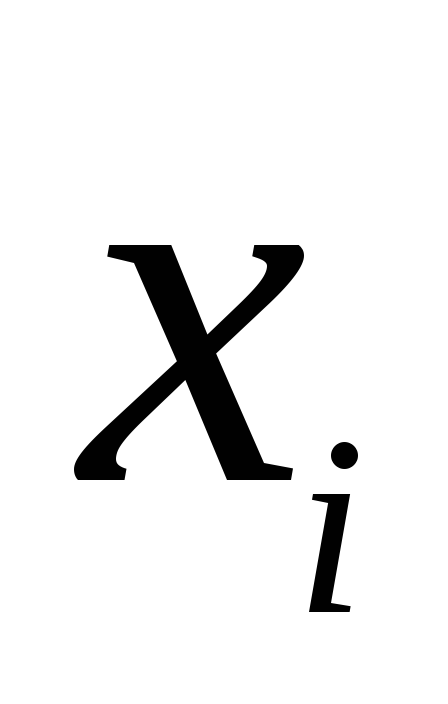
	1	1,2	1,4	1,6	1,8	2,0
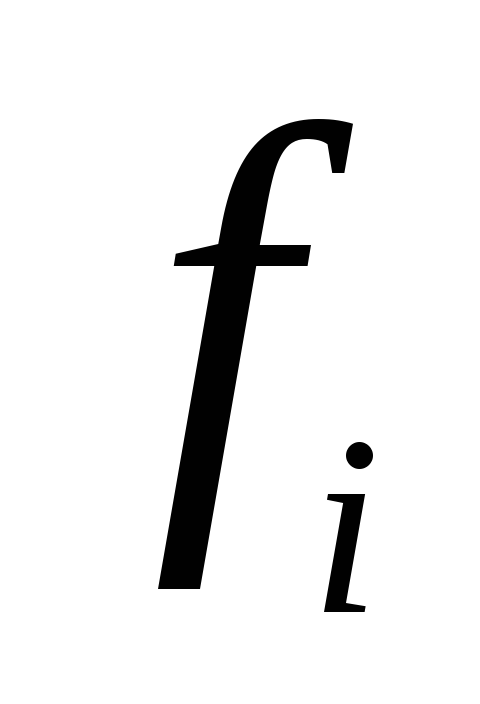
	1,0000000	0,83333333	0,7142857	0,6250000	0,5555555	0,50000000

Розв’язання. За умовою , 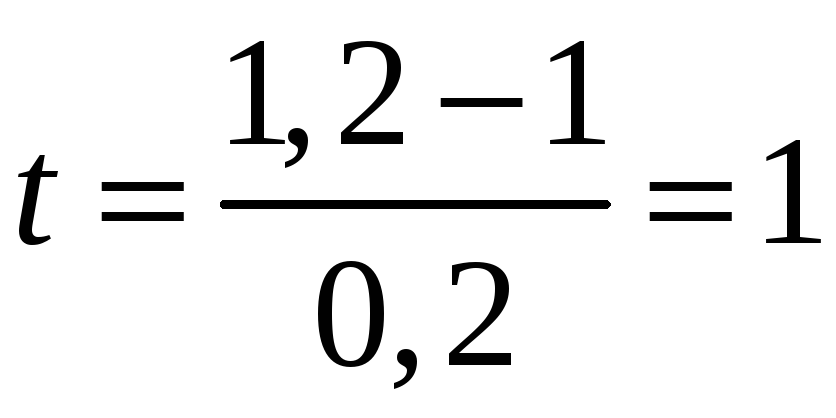. Для випадку чотирьох вузлів інтерполяції (), отримаємо наступну апроксимацію першої похідної при , , , :

.
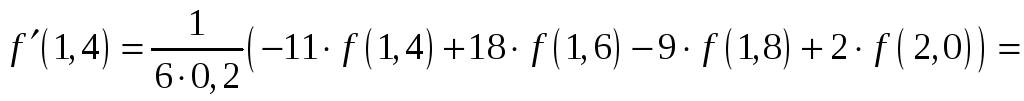
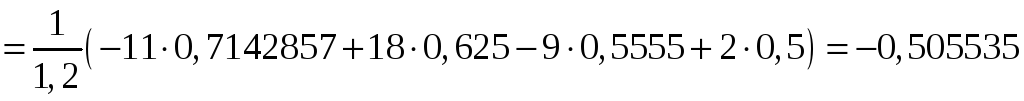