5. Наближення функцій, заданих таблично, методом найменших квадратів

Нехай функція задана своїми значеннями в різних точках з відрізку , які позначимо , . І нехай за апроксимуючу функцію взято многочлен .

За міру відхилення многочлена від даної функції на множині точок приймають величину

,

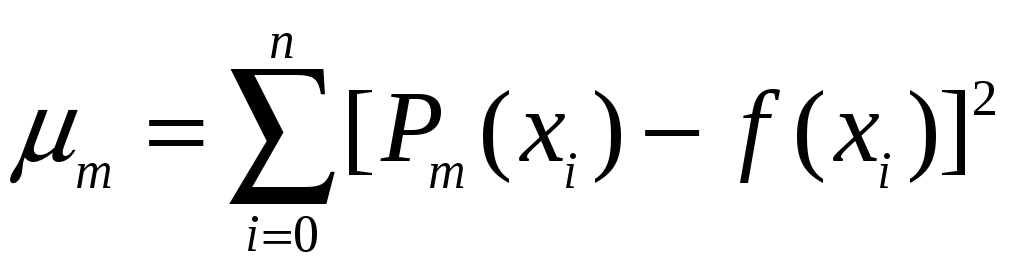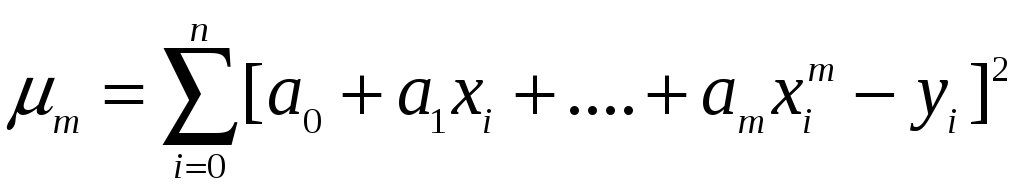, де .

яка дорівнює сумі квадратів відхилень значень від значень функції на заданій системі точок.

Очевидно, що є функцією коефіцієнтів :

.

Ці коефіцієнти треба підібрати так, щоб величина була найменшою. В цьому і полягає метод найменших квадратів. Отриманий при цьому многочлен називається апроксимуючим для даної функції, а процес побудови цього многочлена називається точковою квадратичною апроксимацією.

В теорії ймовірностей доводиться, що отримані таким методом значення параметрів найбільш ймовірні, якщо відхилення підлягають нормальному закону розподілу.

Щоб дослідити функцію на мінімум, знайдемо її частинні похідні по всім змінним і прирівняємо їх нулю:

, , …, .

;

;

……………………………………………………………

.

;

;

……………………………………………………………

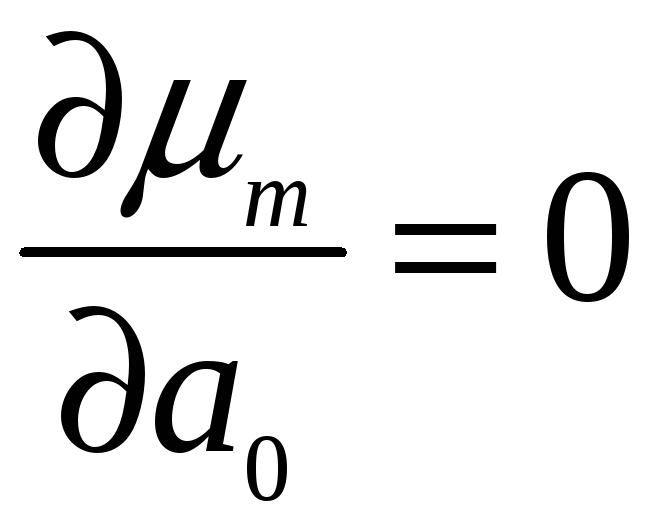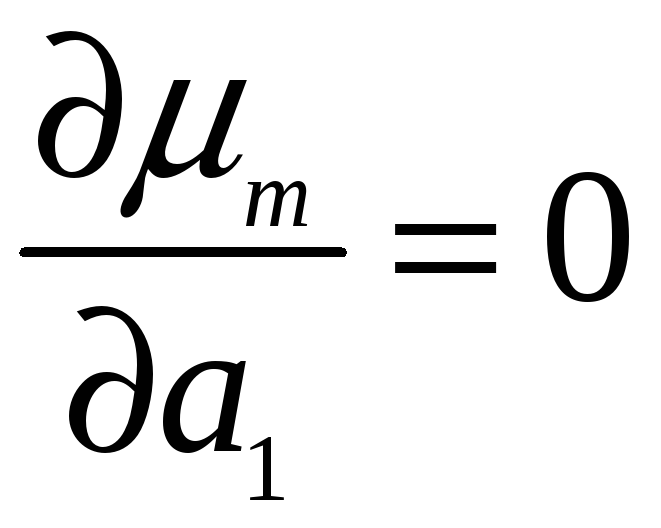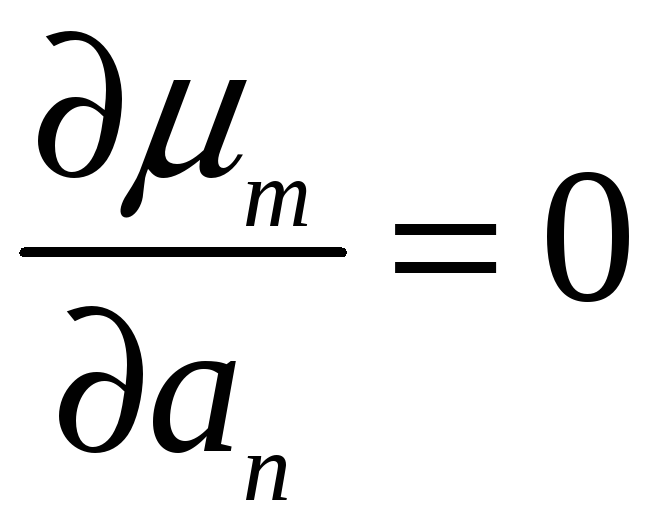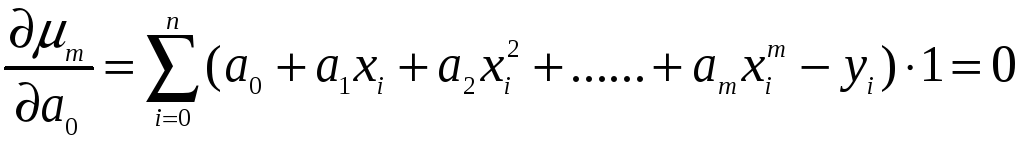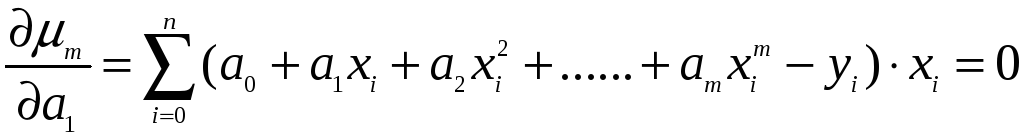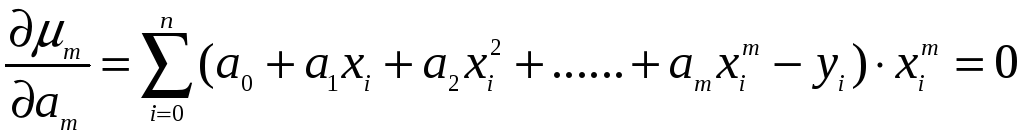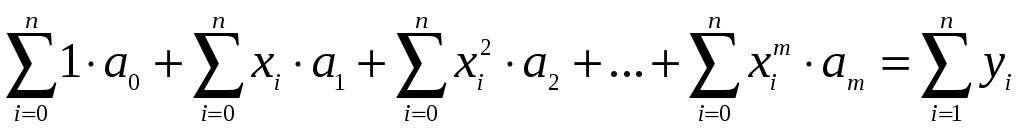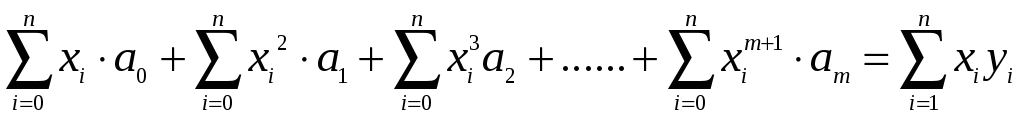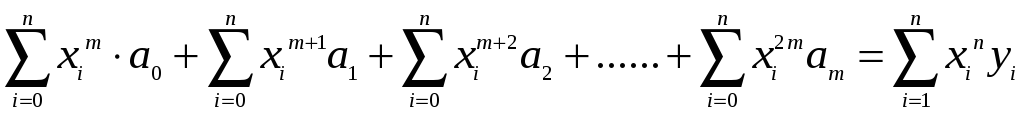
Введемо позначення:

()

()

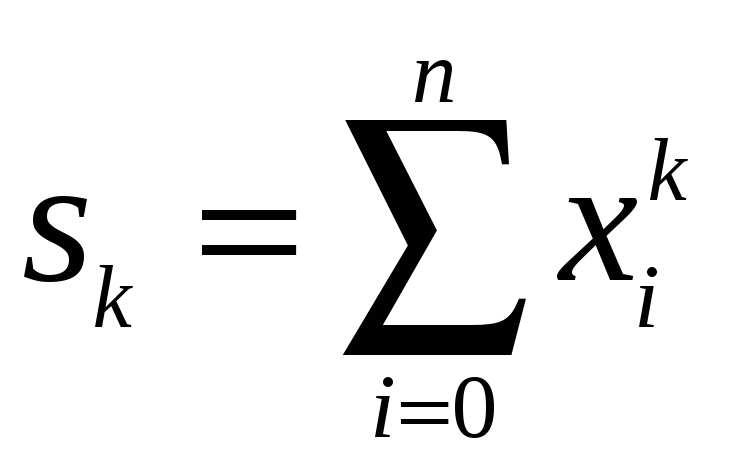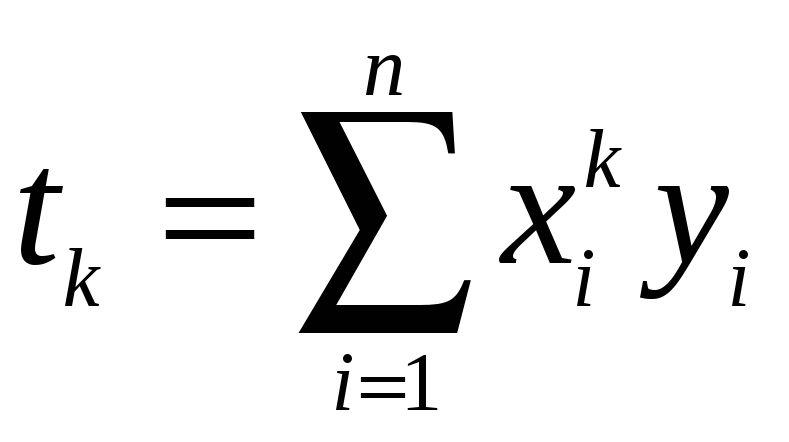Тоді отримаємо систему лінійних алгебраїчних рівнянь:

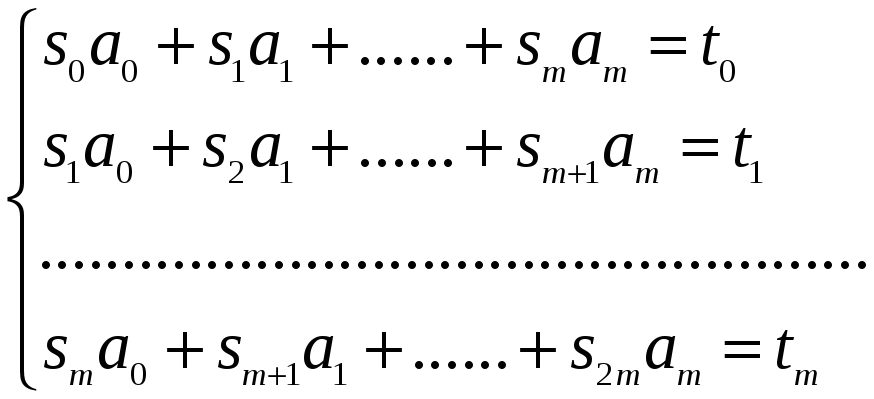(10)

Можна довести, що якщо серед точок немає співпадаючих і , то визначник цієї системи відмінний від нуля і, отже, ця система має єдиний розв'язок. Інтерполяційний многочлен з такими коефіцієнтами і буде мати мінімальне квадратичне відхилення.

Середньоквадратична похибка

.

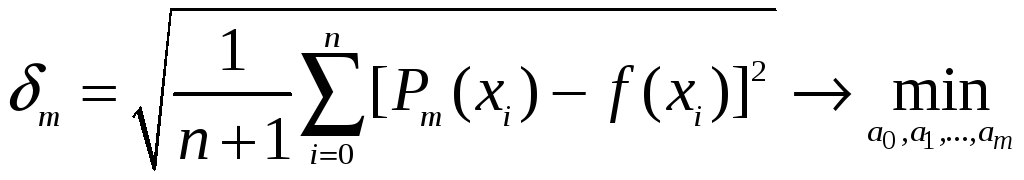Якщо , то апроксимуючий многочлен збігається з інтерполляційним многочленом Лагранжа для системи точок , причому .

Алгоритм наближення функції, заданої таблично, методом найменших квадратів

1. Обчислити коефіцієнти 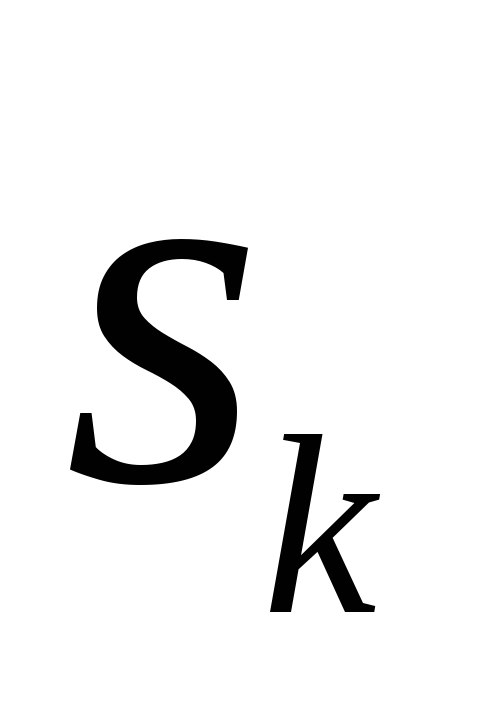, , 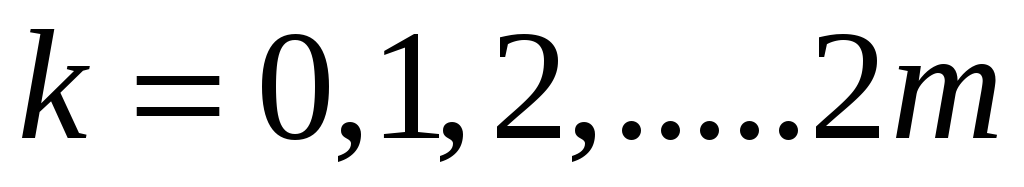, , 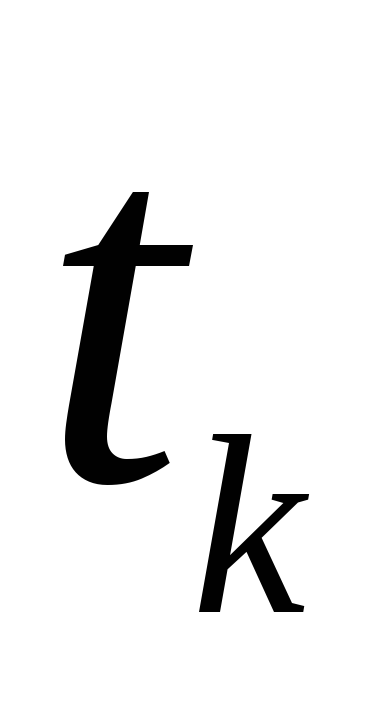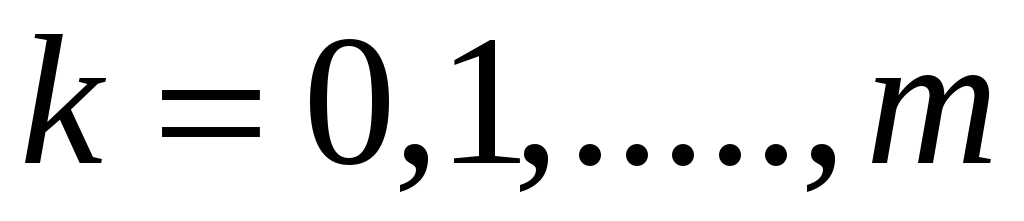по заданій таблицею функції і записати систему лінійних алгебраїчних рівнянь (10)

2. Розв’язати отриману систему лінійних алгебраїчних рівнянь і знайти коефіцієнти .

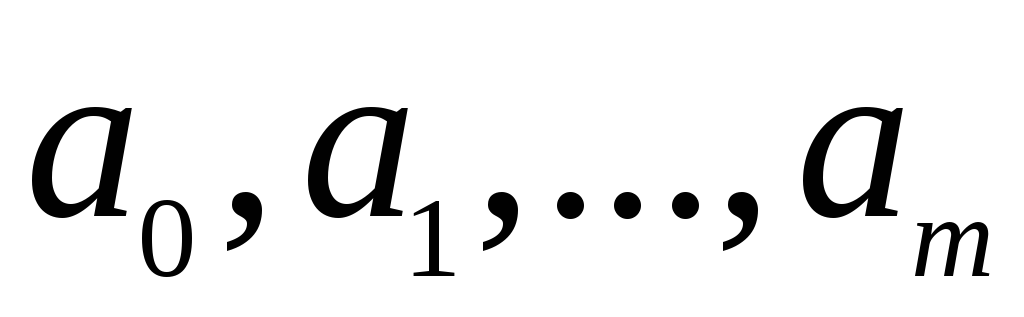3. Записати шуканий апроксимуючий многочлен.

Приклад 3. Застосовуючи метод найменших квадратів, наблизити функцію , заданої таблицею своїх значень, многочленами а) 1-ого й б) 2-ого степенів. Для кожного наближення визначити величину середньоквадратичної похибки. Побудувати точковий графік функції і графіки многочленів.

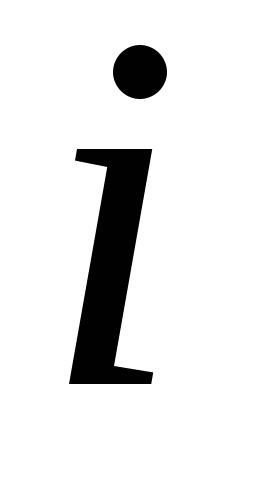
	0	1	2	3
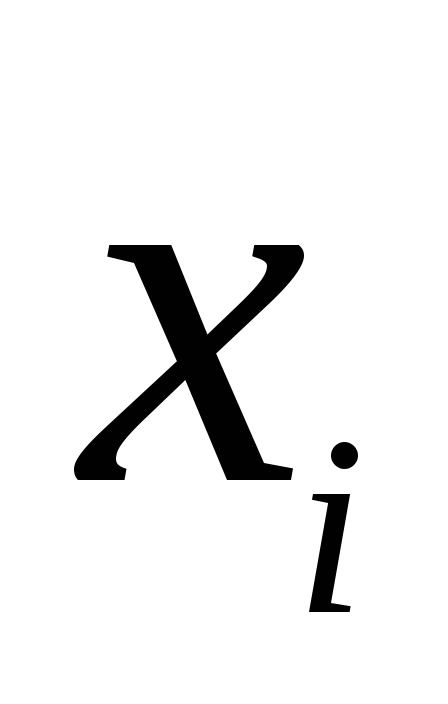
	2	3	4	5
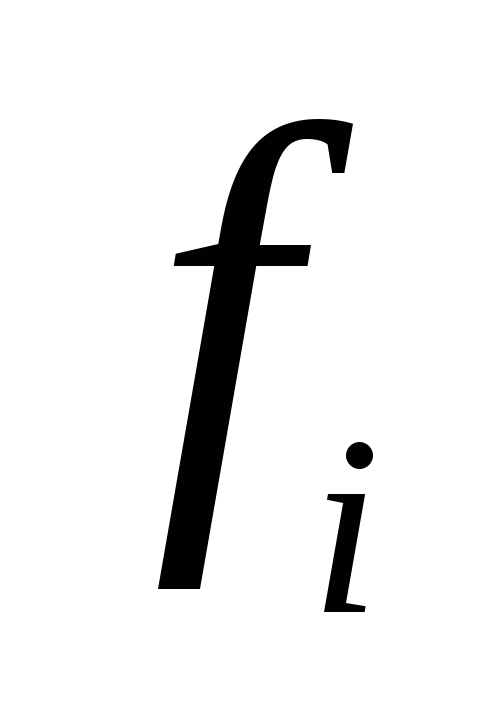
	7	5	8	7

Розв’язання. а) Нехай степінь апроксимуючого многочлена , тоді він матиме вигляд:

.

1. Для обчислення коефіцієнтів системи

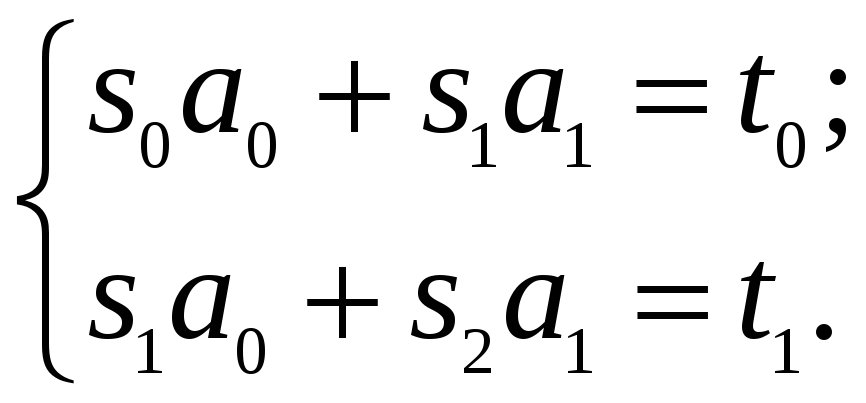
побудуємо розрахункову таблицю:

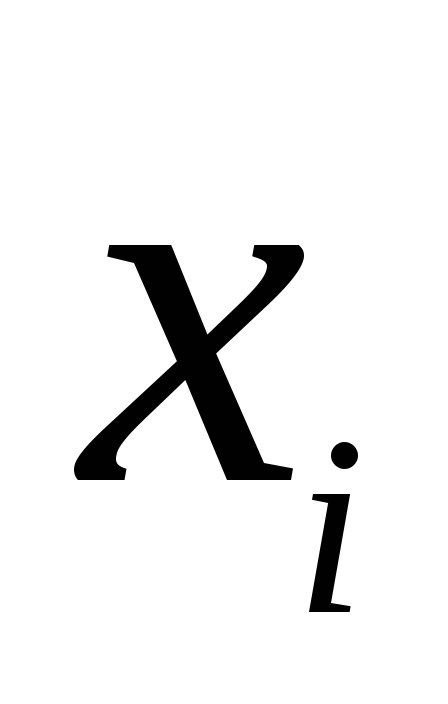
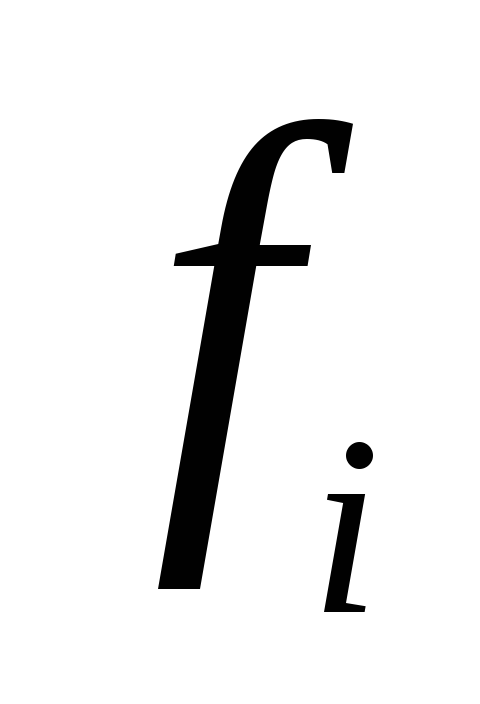
		1
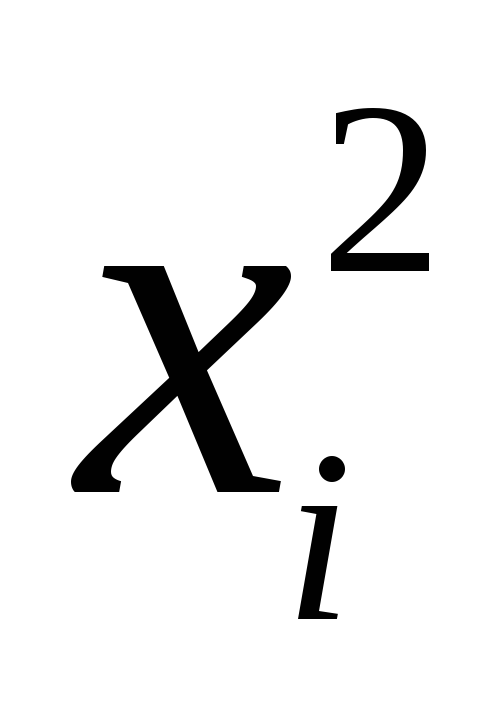
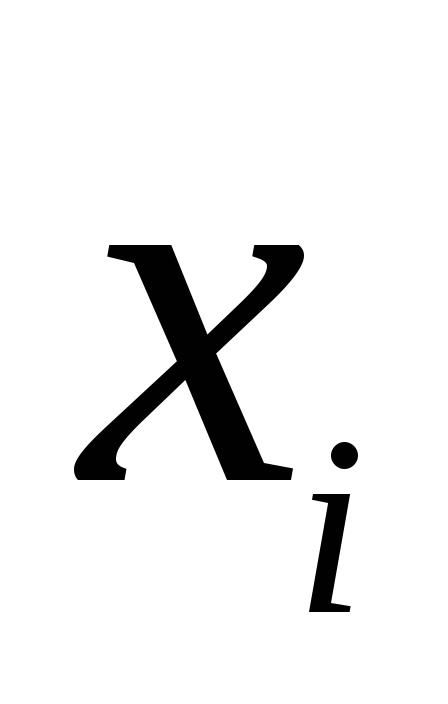
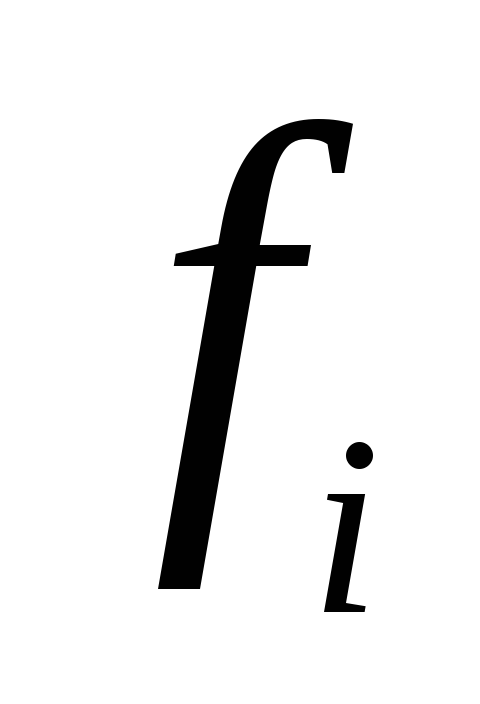
2	7	1	4	14
3	5	1	9	15
4	8	1	16	32
5	7	1	25	35
14	27	4	54	96

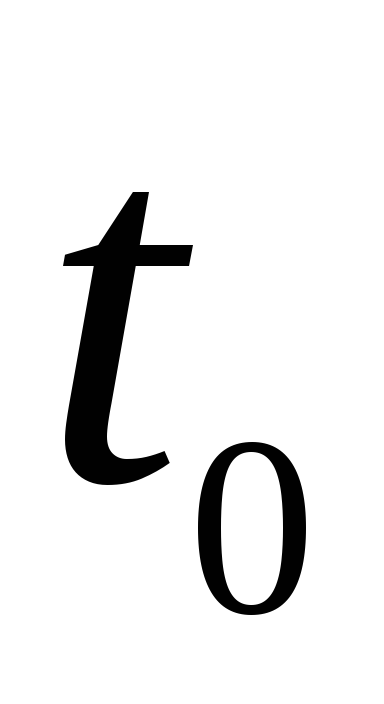
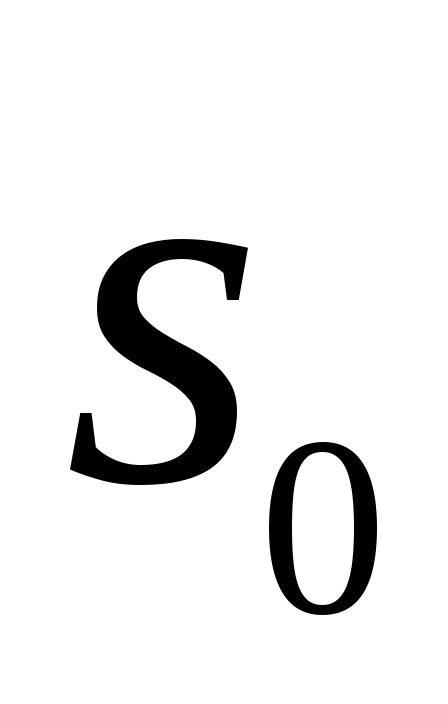
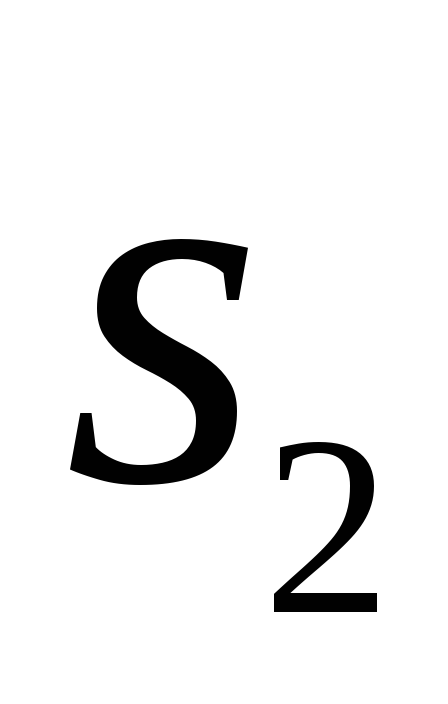
В результаті одержуємо:

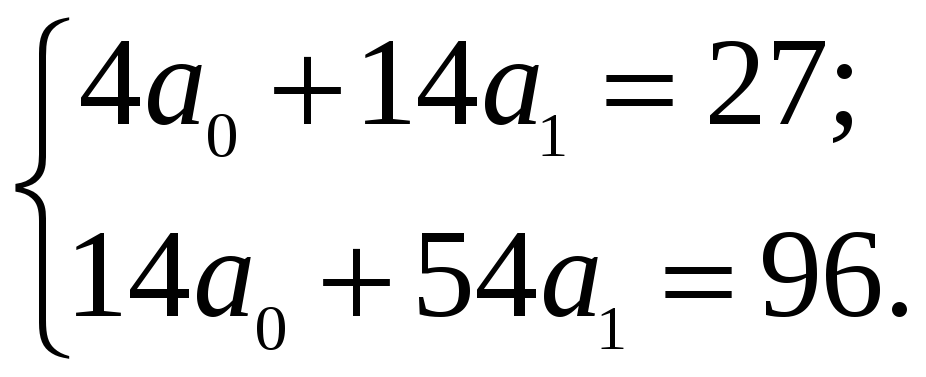
2. Розв’язуємо отриману систему лінійних алгебраїчних рівнянь:

, .

3. Шуканий апроксимуючий многочлен має вигляд:

.

Визначимо середньоквадратичну похибку

.

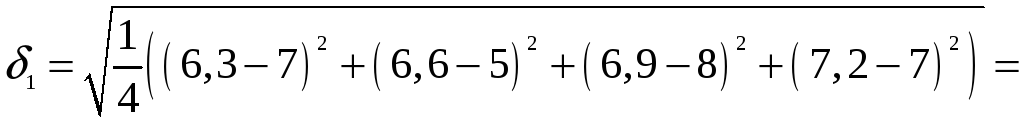
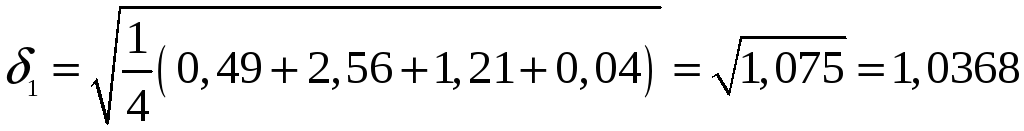б) Нехай степінь апроксимуючого многочлена , тоді він матиме вигляд:

.

1. Для обчислення коефіцієнтів системи

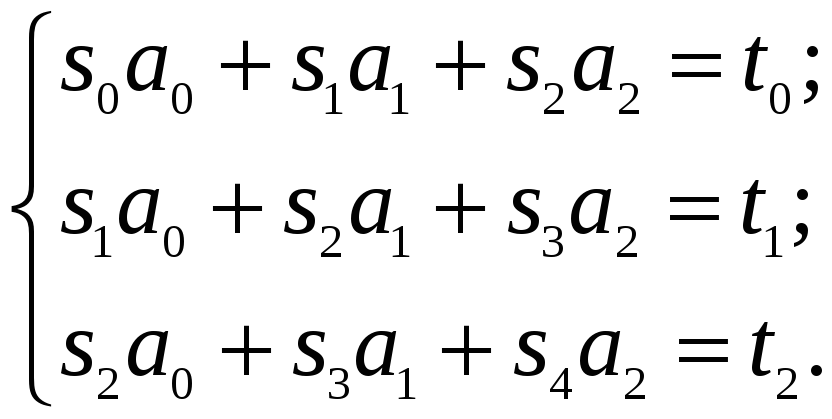
побудуємо розрахункову таблицю:

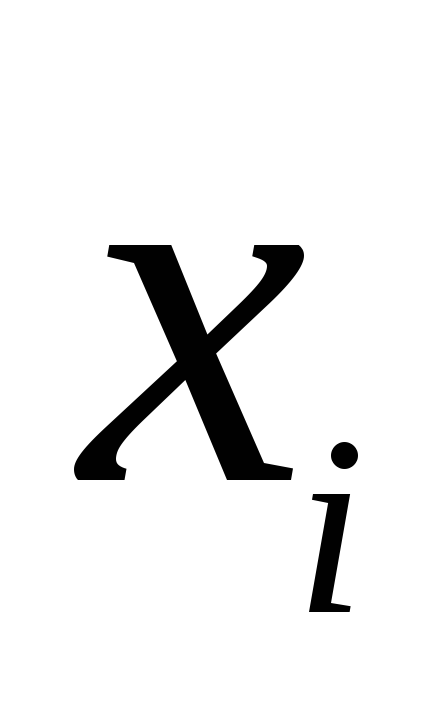
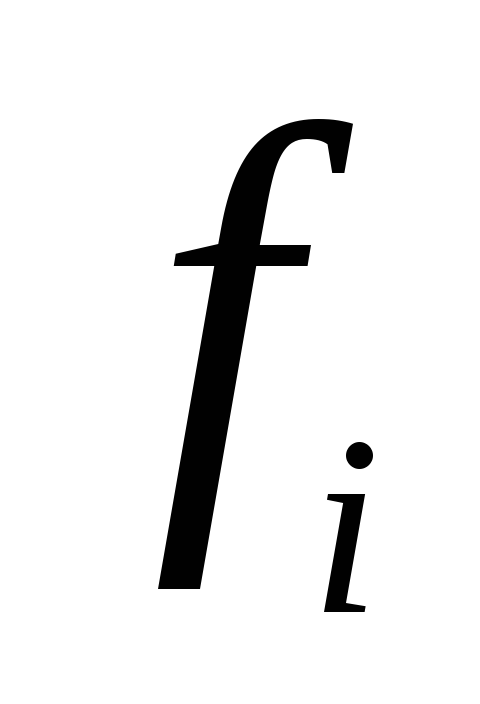
		1
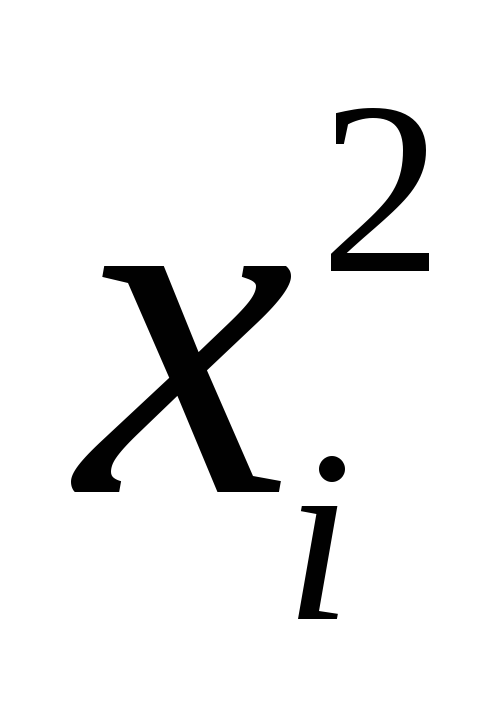
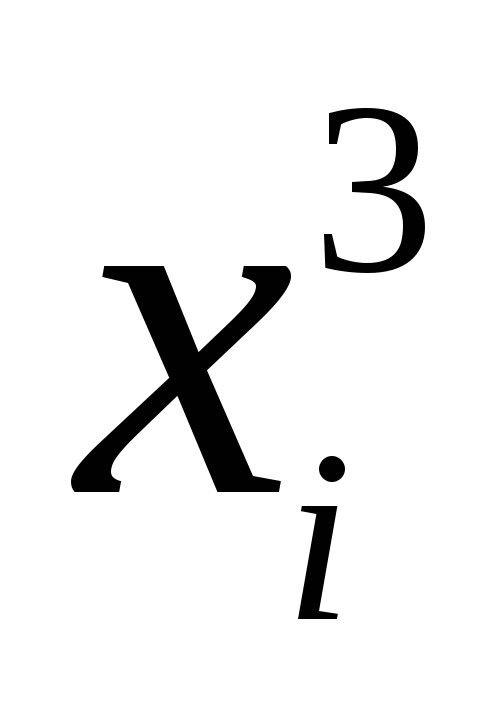
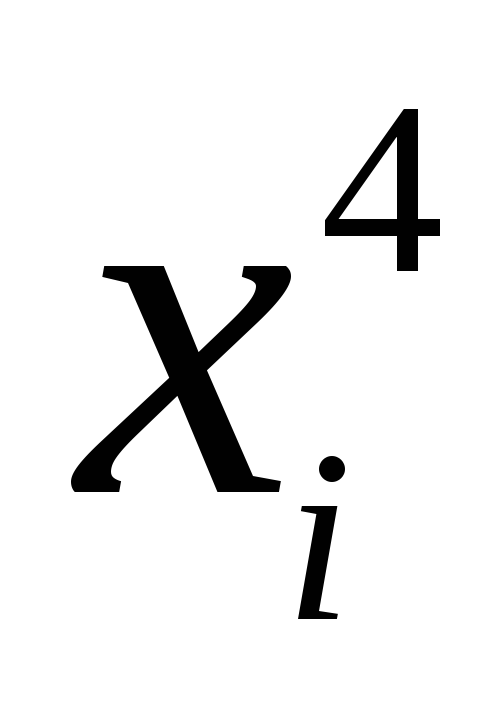
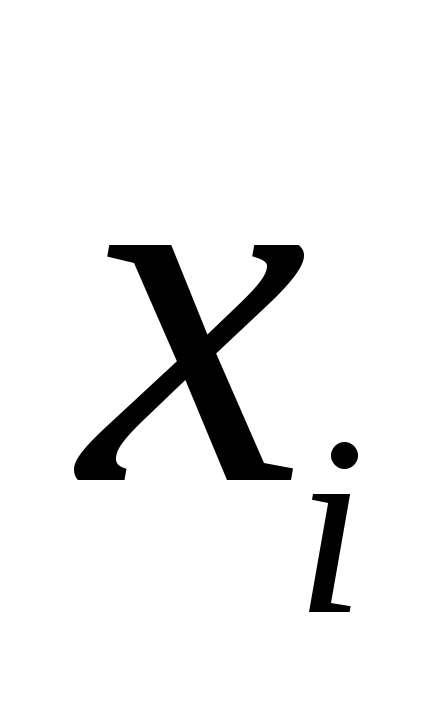
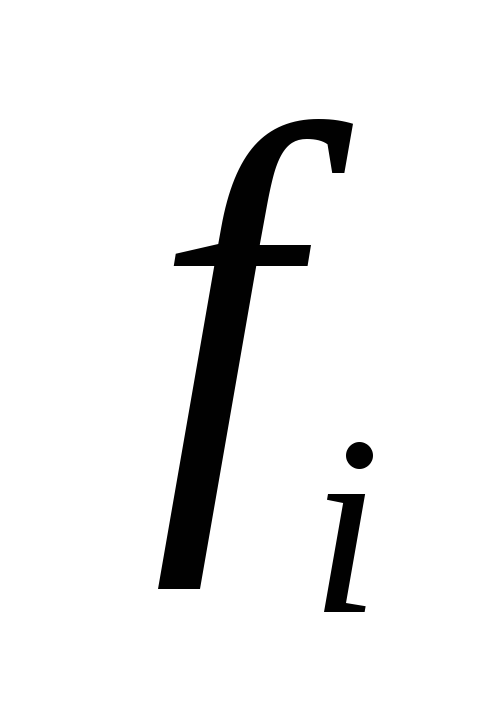
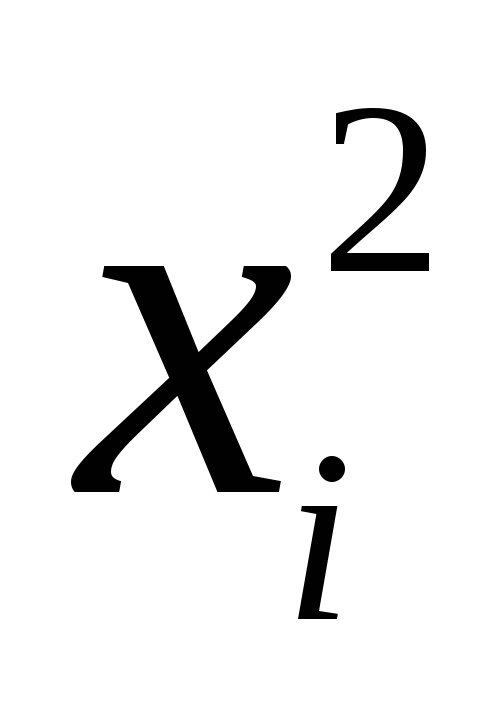
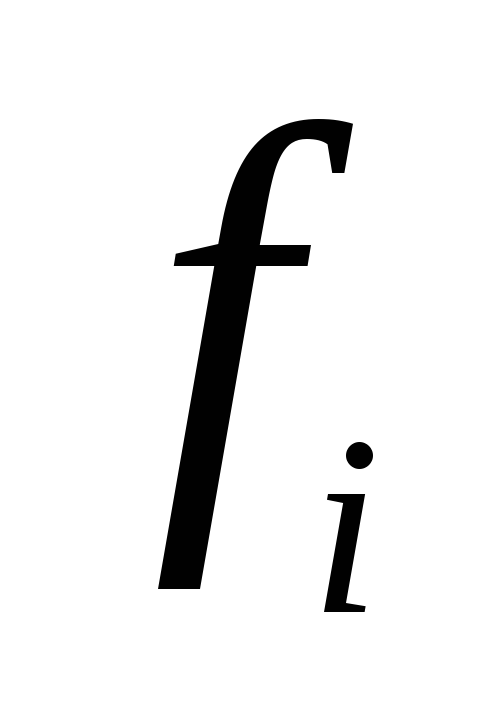
2	7	1	4	8	16	14	28
3	5	1	9	27	81	15	45
4	8	1	16	64	256	32	128
5	7	1	25	125	625	35	175
14	27	4	54	224	978	96	376

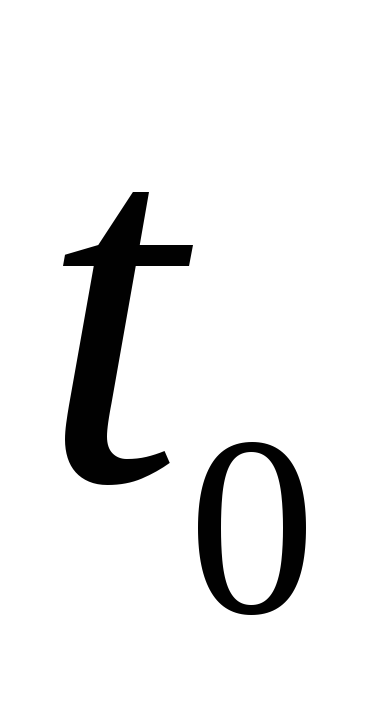
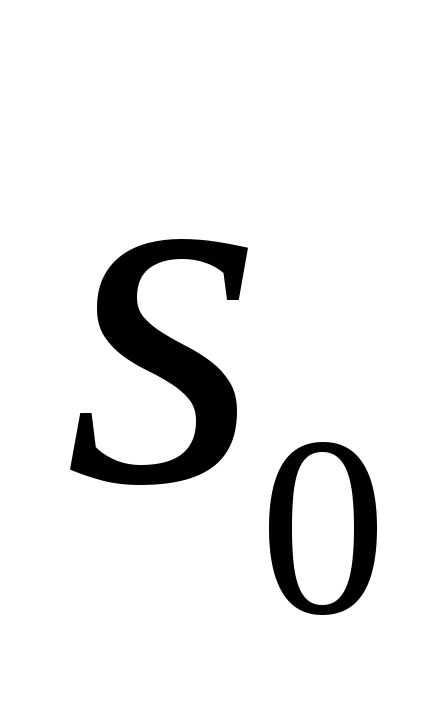
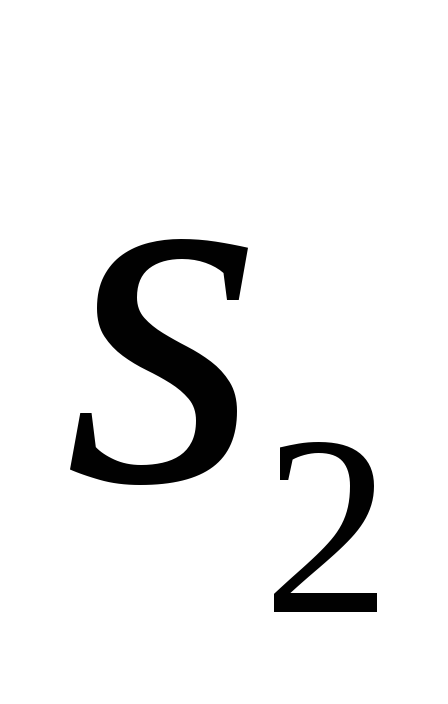
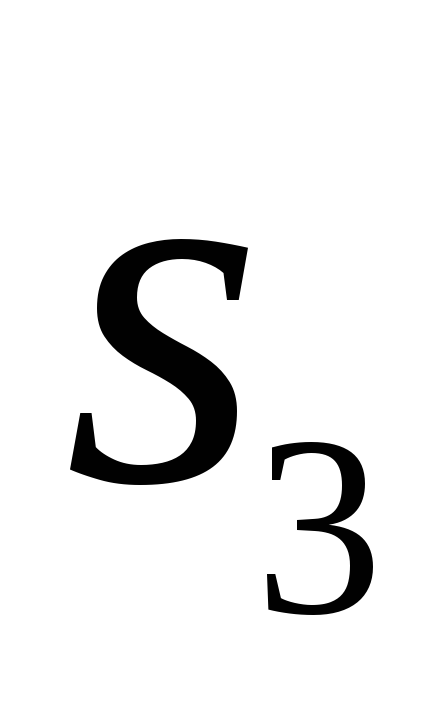
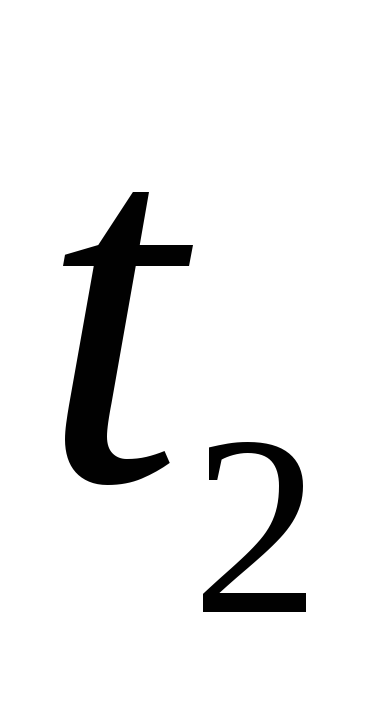
В результаті одержуємо:

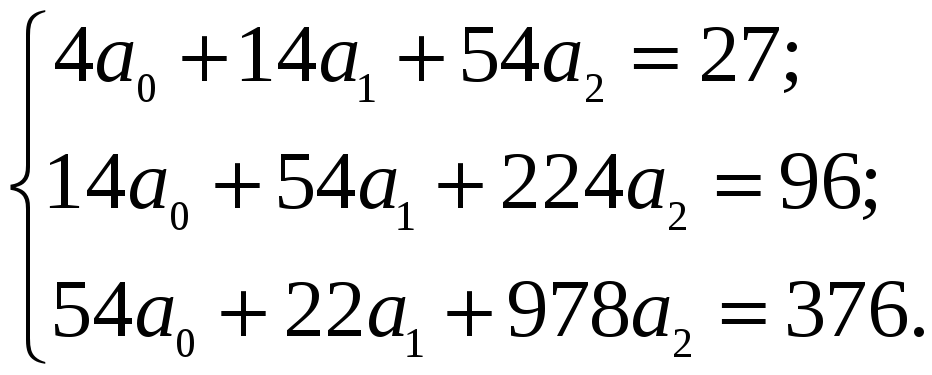
2. Розв’язуємо отриману систему лінійних алгебраїчних рівнянь:

, , .

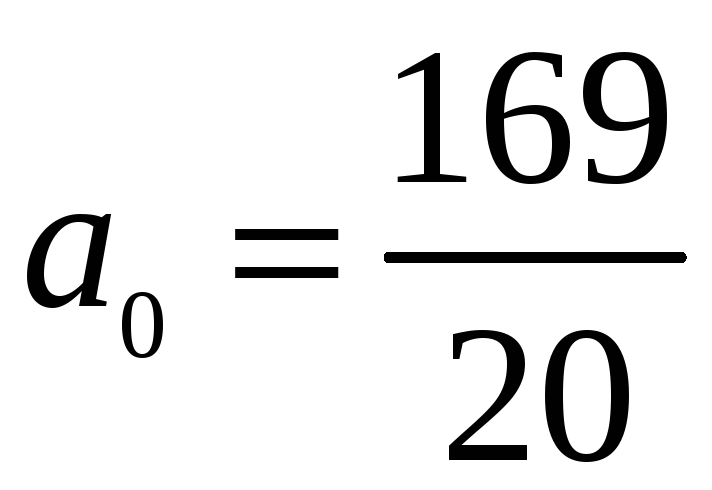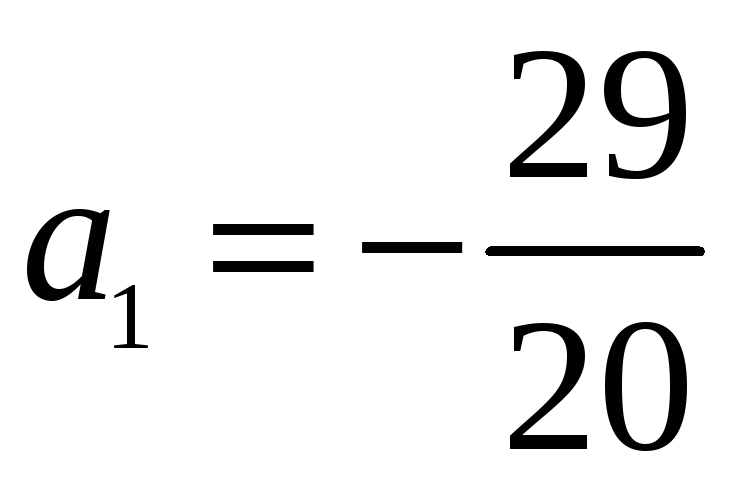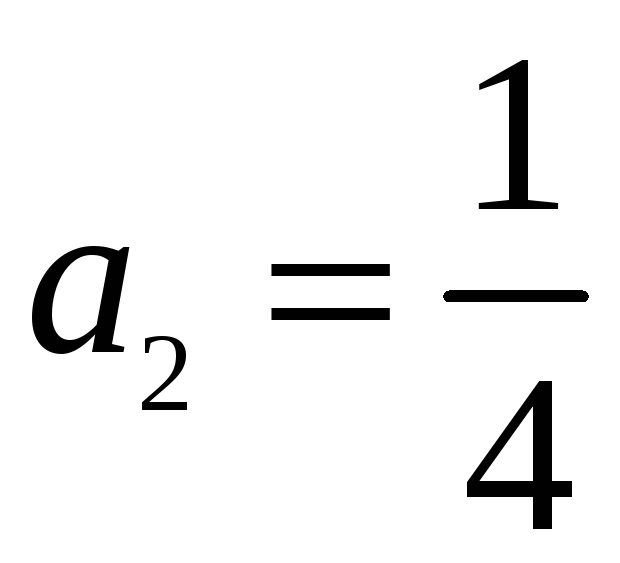3. Шуканий апроксимуючий многочлен має вигляд:

.

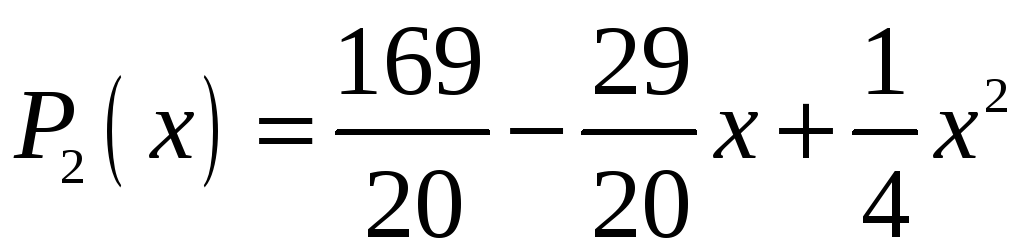Визначимо середньоквадратичну похибку

.

Побудуємо точковий графік функції і графіки многочленів.

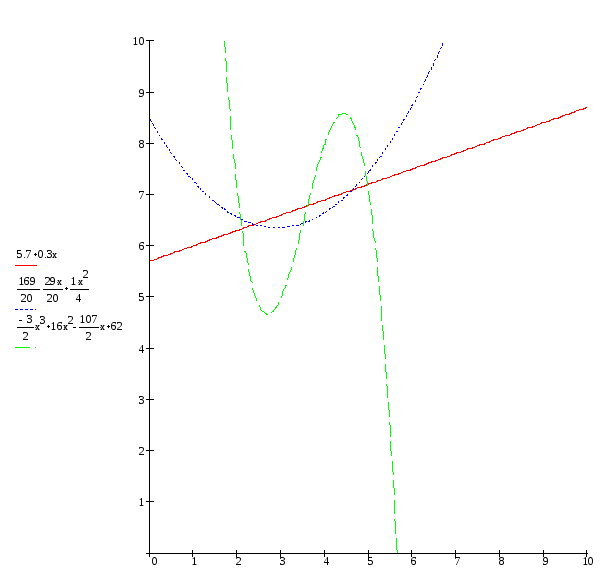
На малюнку зображені точковий графік функції і графіки апроксимуючих многочленів при і при , а також інтерполяційний многочлен, отриманий в прикладах 1 і 2 ().