3. Похибка інтерполяції многочленом Лагранжа

При визначенні значення , , для функції , за допомогою многочлена Лагранжа виникає похибка інтерполяції :

. (6)

Якщо відносно функції нічого не відомо, крім її значень у вузлах інтерполяції, то ніяких корисних висновків відносно похибки зробити неможливо. Одержимо вираз похибки інтерполяції у припущенні, що , тобто – функція неперервна разом зі своїми похідними на відрізку , що містить всі вузли інтерполяції , ,і точку .

Теорема. Якщо , відрізок містить всі вузли інтерполяції, то для довільного значення

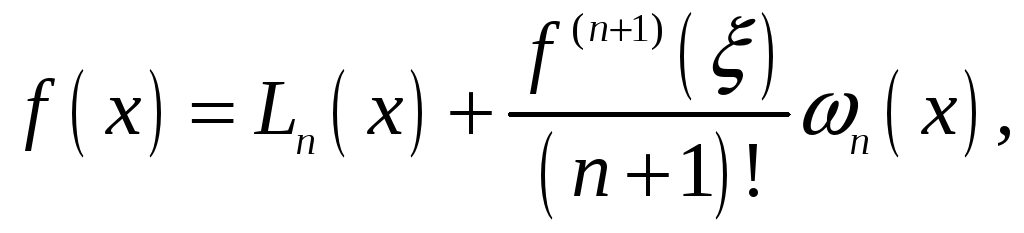, (7)

де – многочлен -го степеня, а – деяка невідома точка.

З формули (7) одержуємо оцінку похибки інтерполяції в деякій довільній фіксованій точці :

,

та оцінку максимальної похибки на усьому відрізку :

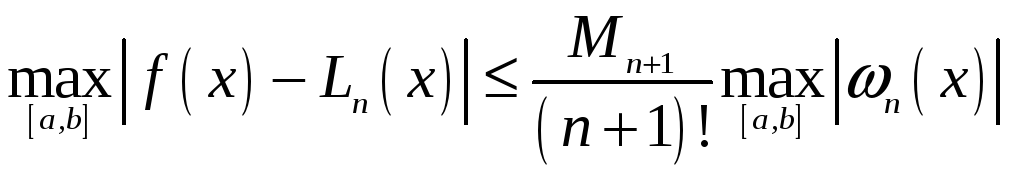
де .

Інтерполяція многочленом Лагранжа з рівновіддаленими вузлами

Розглянемо особливості побудови інтерполяційного многочлена Лагранжа у випадку рівномірного розподілу вузлів.

Нехай , , – вузли інтерполяції, – крок, – задані значення функції , причому .

Введемо безрозмірну незалежну змінну

,

Тоді вузлу відповідає

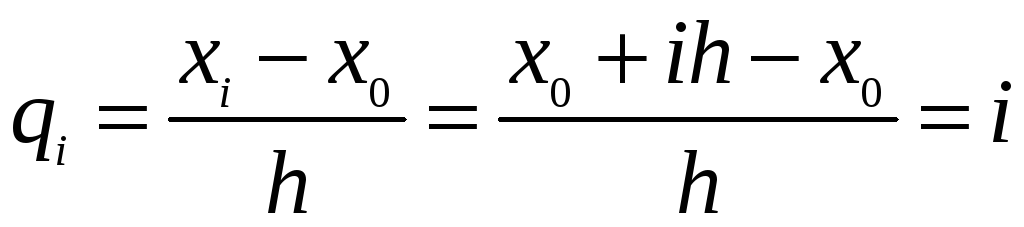
і, окрім того, виконуються співвідношення

,

При цьому інтерполяційний многочлен Лагранжа, що відповідає випадку записується у вигляді:

.

У загальному випадку інтерполяційний многочлен Лагранжа (4)

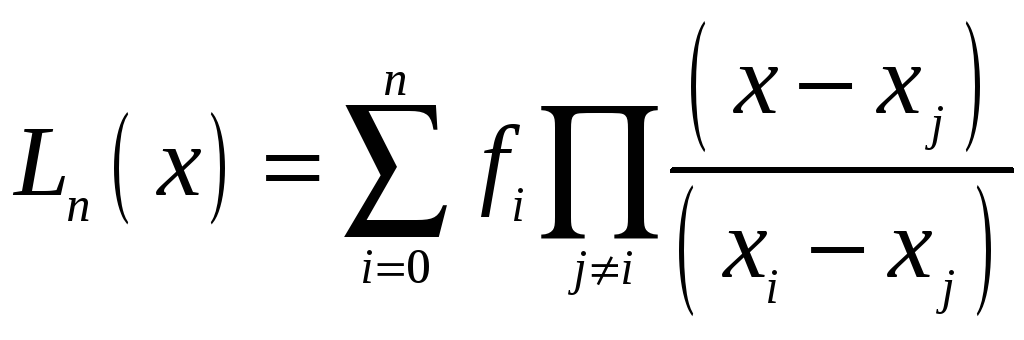
одержить наступний вигляд:

,

де

.

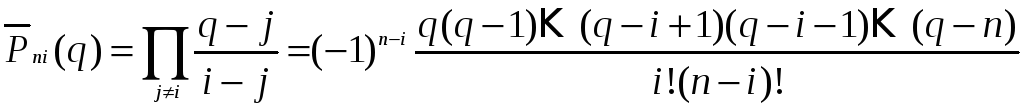Оскільки

,

де ,

залишковий член інтерполяційного многочлена може бути поданий у вигляді

.

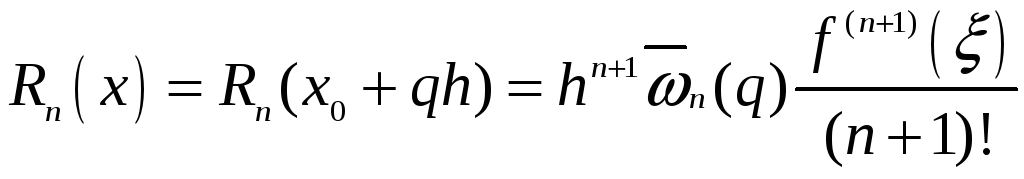Зауважимо, що з означення виходить, що зміні змінної на відрізку відповідає зміна змінної на відрізку . Тому оцінку максимальної похибки інтерполяції на відрізку можна записати у наступному вигляді:

,

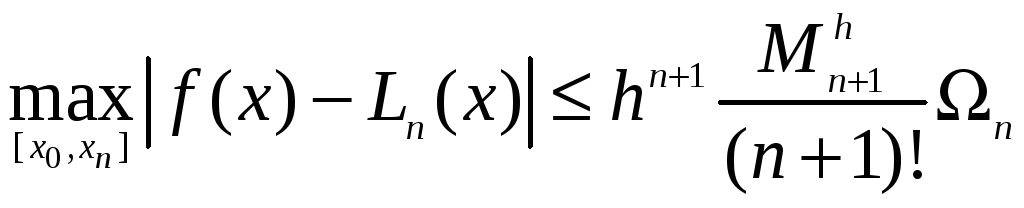де .

Величина не залежить від . Її можна заздалегідь обчислити чи оцінити. Зокрема, .

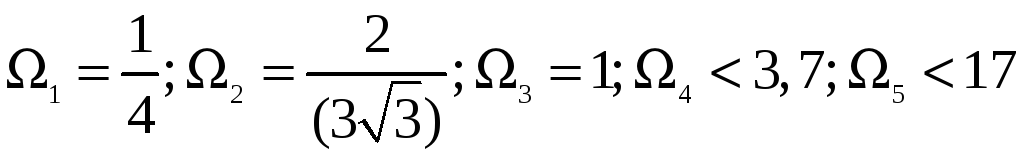Враховуючи, що , можна зробити висновок, що максимальна похибка інтерполяції на відрізку , тобто

.

Зауважимо, що (враховуючи ) при зменшенні кроку вдвічі права частина оцінки зменшиться мінімум у разів.

Виходячи з підсиленої оцінки, що одержується з нерівності , у яку замість підставлене , вибирають крок таблиці значень функції на відрізку з тим щоб забезпечити задану точність інтерполяції. При цьому є ще можливість змінювати у деяких границях ступінь інтерполяційного многочлена. Якщо функція достатньо гладка, то підвищення спочатку, як правило, веде до підвищення припустимого , але, з другого боку, ускладнює інтерполяцію і підсилює вплив неусувних похибок табличних значень. На практиці рідко використовують інтерполяцію з .

Зауваження. При заданому вузли інтерполяції , розташовані з кроком , доцільно вибирати з сукупності усіх вузлів заданої таблиці функції так, щоб точка опинилась як можна ближче до середини відрізку . Це пов’язано з тим, що коливання функцій (та ) поблизу середини згаданого відрізку менше, ніж у його кінців.

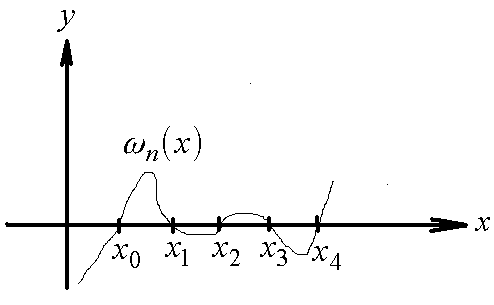
4. Інтерполяційний многочлен Ньютона

Розглянемо побудову інтерполяційного многочлена у випадку рівномірного розподілу вузлів. Нехай , , – крок.

Введемо поняття скінченних різниць. Нехай відомі значення функції у вузлах : . Складемо різниці значень функції:

;

;

……………………………………………….

.

Ці значення називаються першими різницями або різницями першого порядку функції.

Можна скласти другі різниці:

, , …

Аналогічно складаються різниці -го порядку:

, .

Скінченні різниці можна виразити безпосередньо через значення функції:

:

.

Аналогічно для різниці -го порядку:

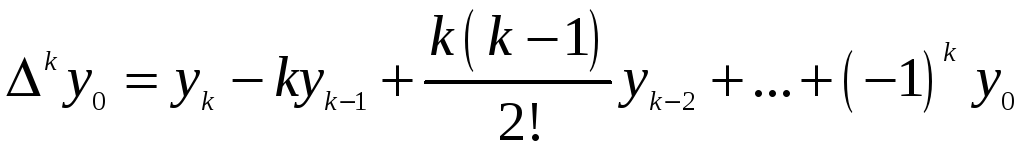(8)

Теорема. Інтерполяційний многочлен може бути записаний у формі

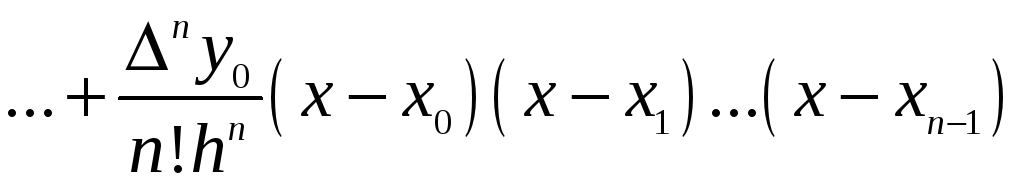. (9)

яка називається інтерполяційним многочленом Ньютона.

Інтерполяційний многочлен Ньютона (9) можна записати у вигляді:

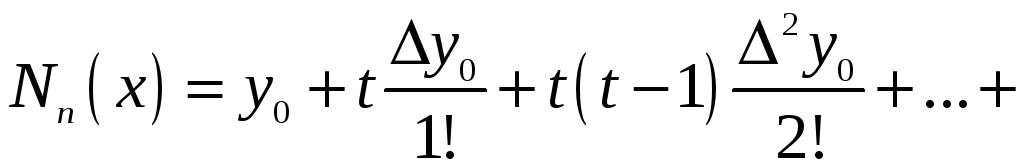
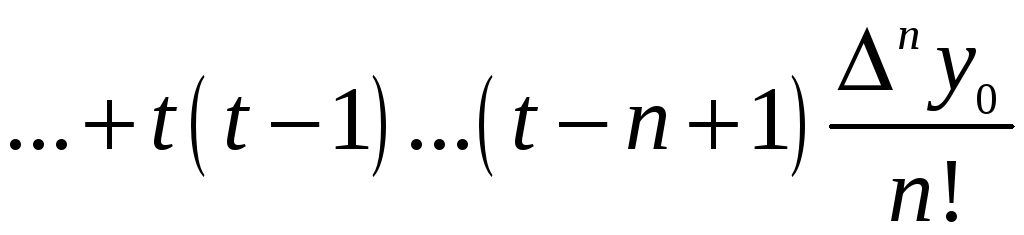, де .

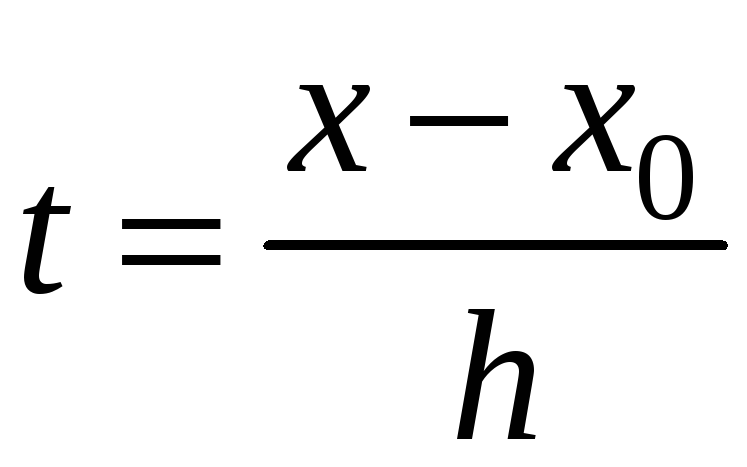Приклад 2. Для функції , заданої таблицею своїх значень, побудувати інтерполяційний многочлен 3-го степеня у формі Ньютона. Обчислити значення функції в точці .

	0	1	2	3
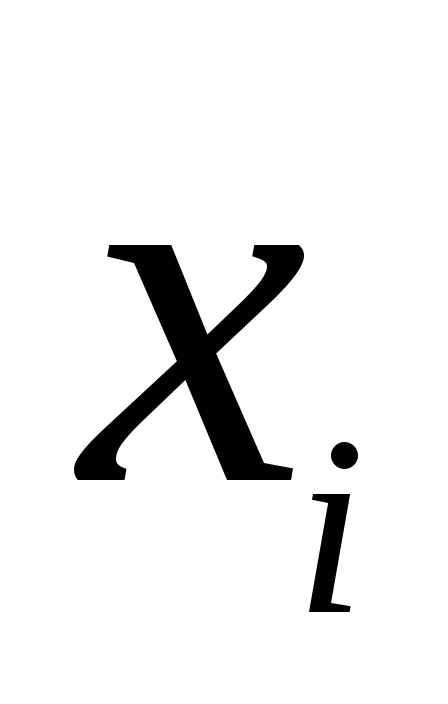
	2	3	4	5
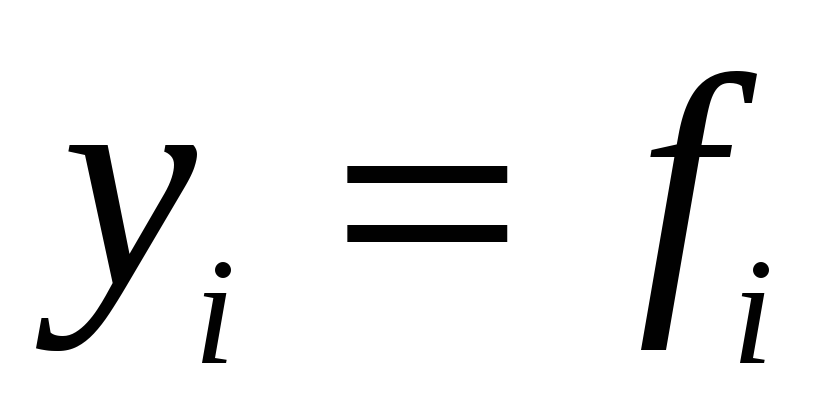
	7	5	8	7

Розв’язання. Побудуємо многочлен Ньютона. Для цього побудуємо таблицю, в якій обчислимо скінченні різниці:

2	7
		–2
3	5		5
		3		–9
4	8		–4
		–1
5	7

За формулою (9) одержимо:

.

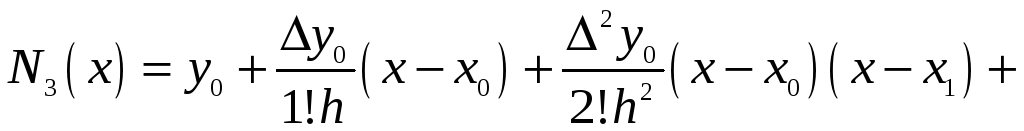
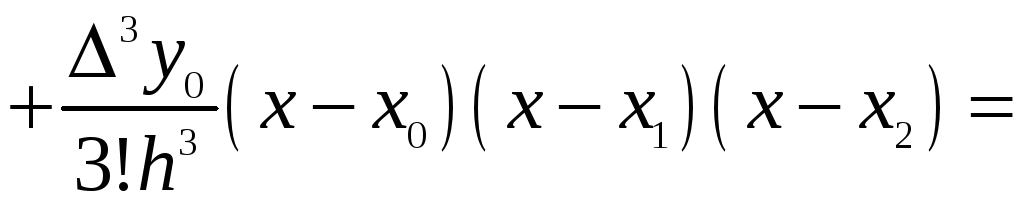
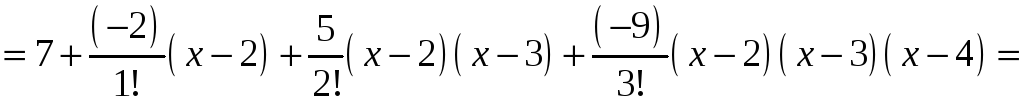
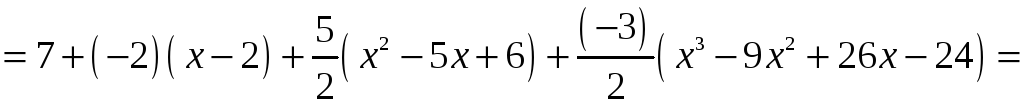
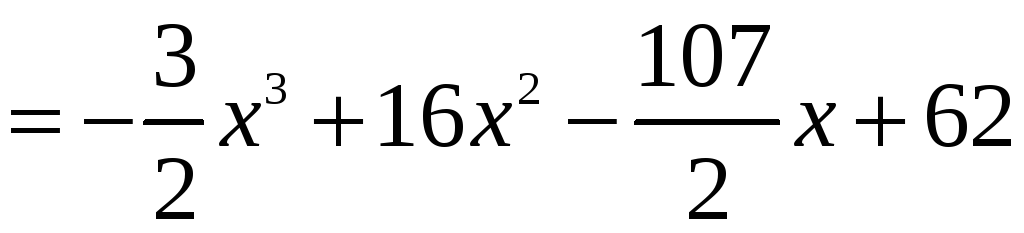Порівнюючи з результатом прикладу 1, можна зробити висновок, що , що підтверджує єдиність розв'язку задачі інтерполяції в класі многочленів, які задовольняють умовам теореми про єдиність розв'язку задачі інтерполяції.