2. Інтерполяційний многочлен Лагранжа

Інтерполяційний многочлен може бути записаний не тільки у формі (2). Існують і інші форми зображення інтерполяційного многочлена, які можна записати одразу через вихідні дані задачі, тобто через , , не розв'язуючи систему (3).

Теорема. Інтерполяційний многочлен може бути записаний у формі

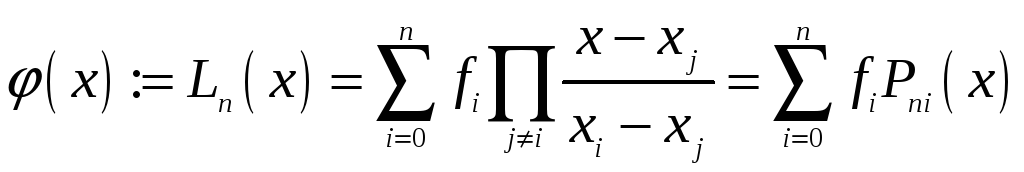(4)

яка називається інтерполяційним многочленом Лагранжа.

Коефіцієнти

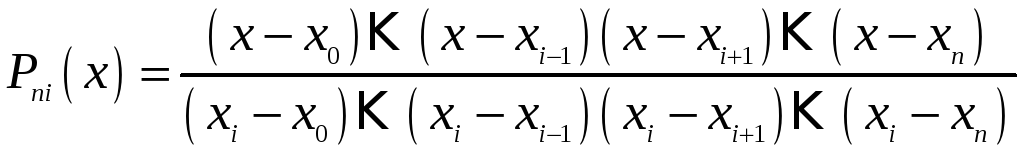
многочлена (4) називаються коефіцієнтами Лагранжа або лагранжевими коефіцієнтами.

Єдиність зображення інтерполяційного многочлена у вигляді (4) випливає з єдиності розв'язку системи лінійних алгебраїчних рівнянь (3).

Досить поширеними випадками З формули (4) можна отримати вирази для лінійної () і квадратичної () інтерполяції.

При маємо многочлен першого степеня:

;

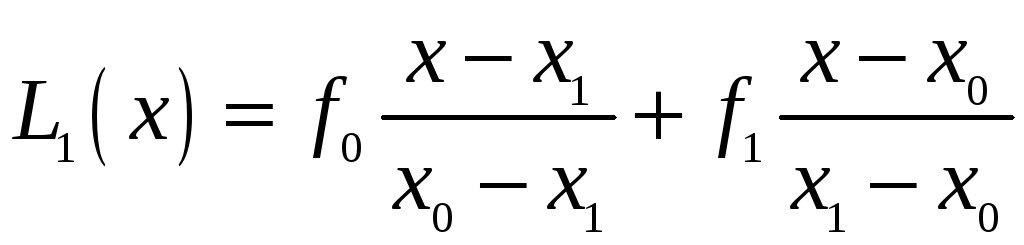При маємо многочлен другого степеня:

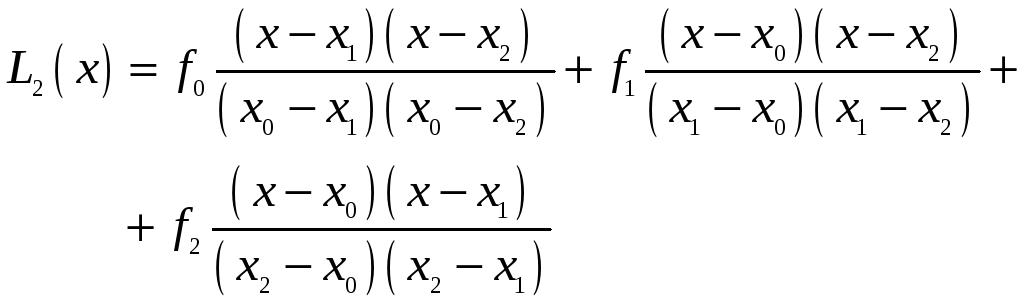
Зауважимо, що оскільки інтерполяційний многочлен (4) лінійно залежить від значень функції , то інтерполяційний многочлен суми двох функцій дорівнює сумі інтерполяційних многочленів доданків (коли вузли інтерполяції збігаються).

Для запису інтерполяційного многочлена Лагранжа зручно користуватися таблицею:

			…
			…
			…
…	…	…	…	…	…	…
			…

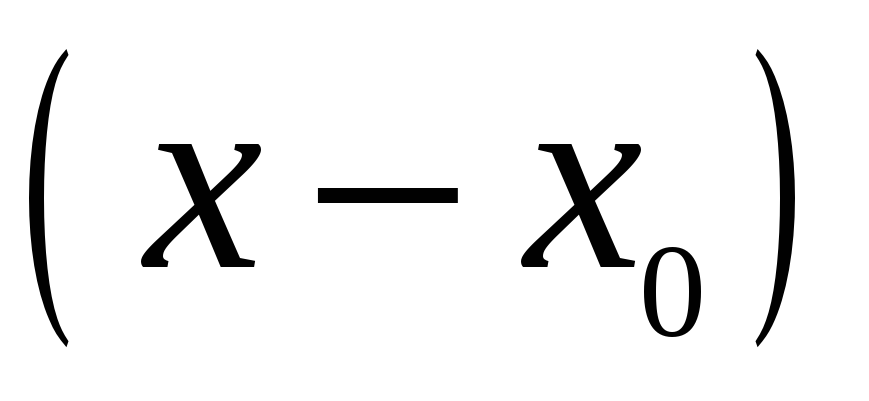
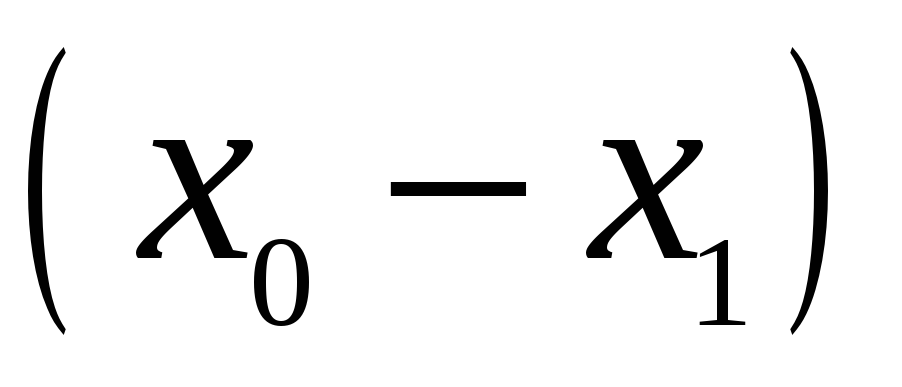
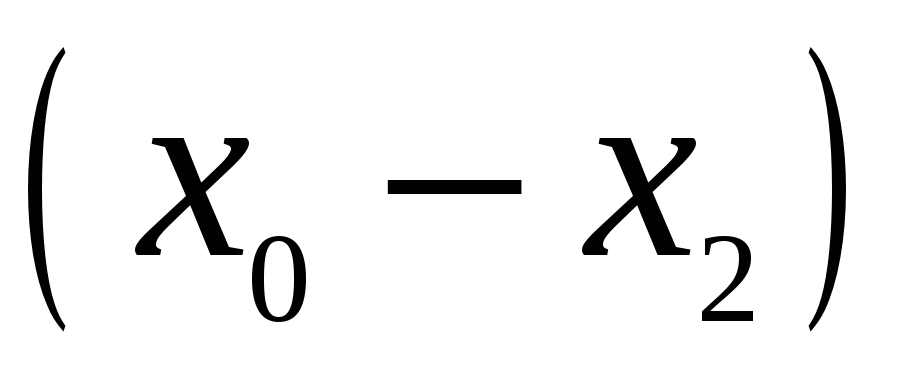
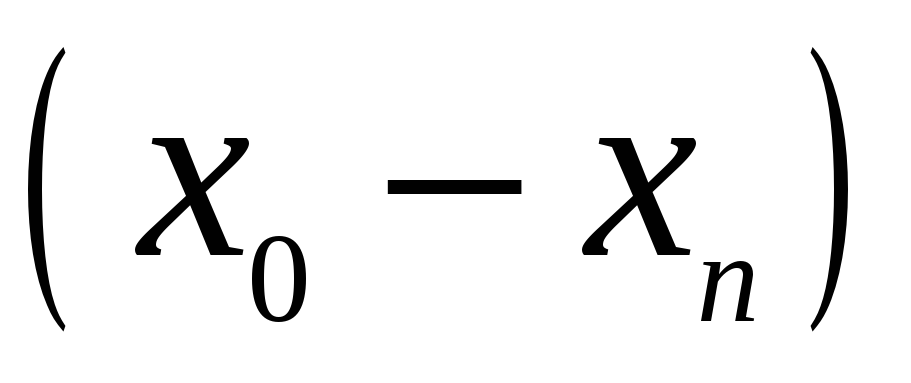
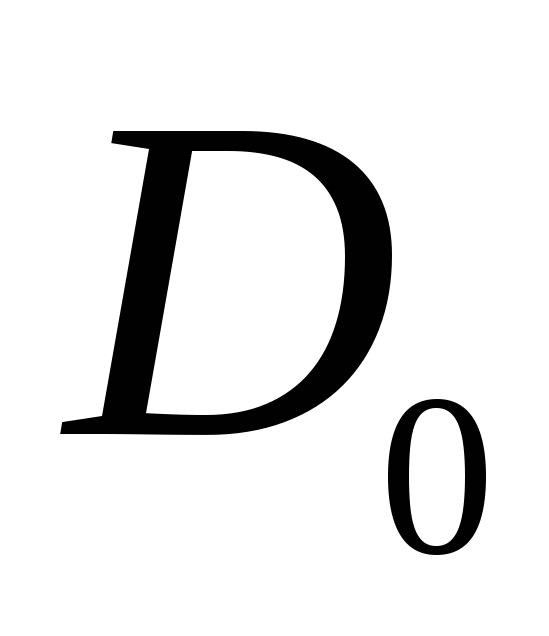
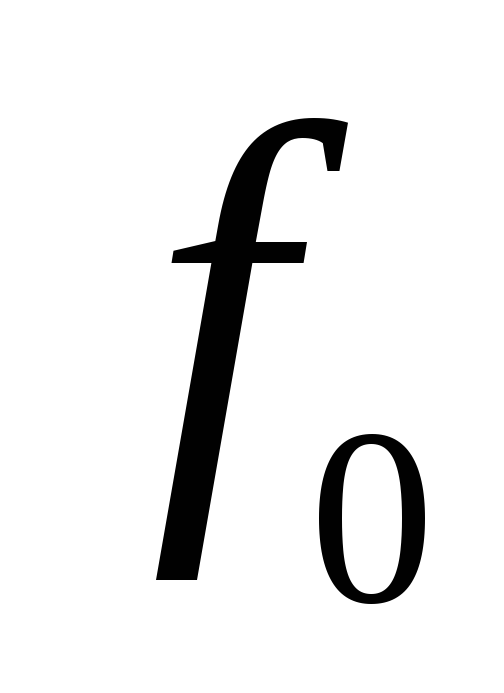
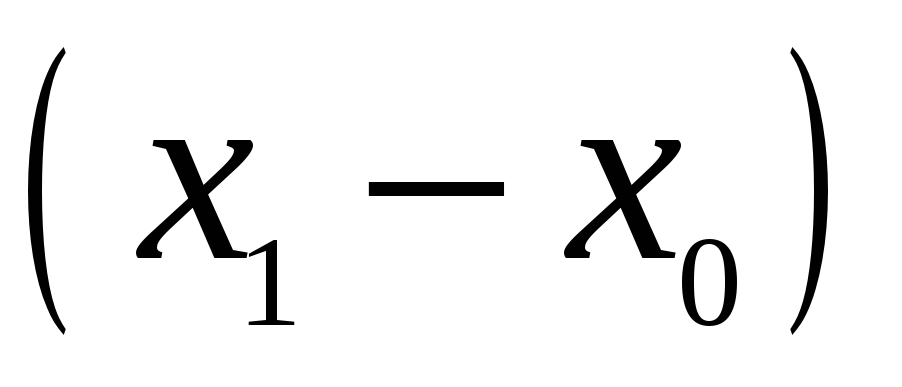
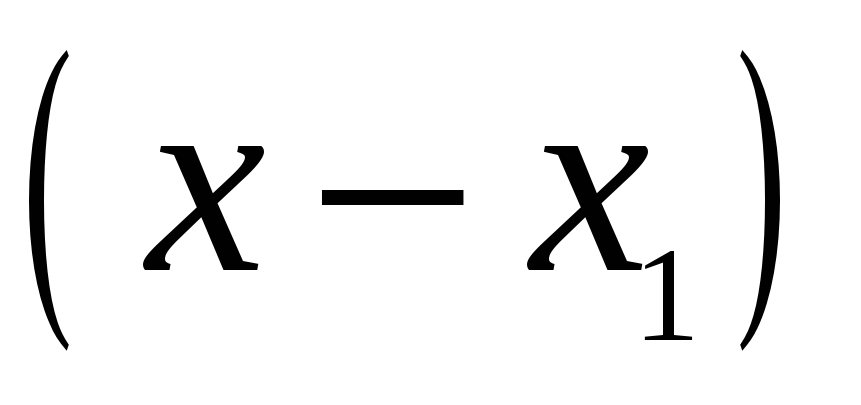
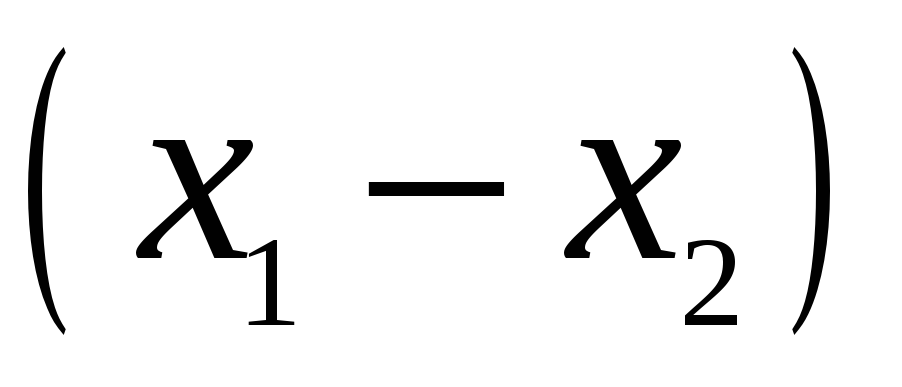
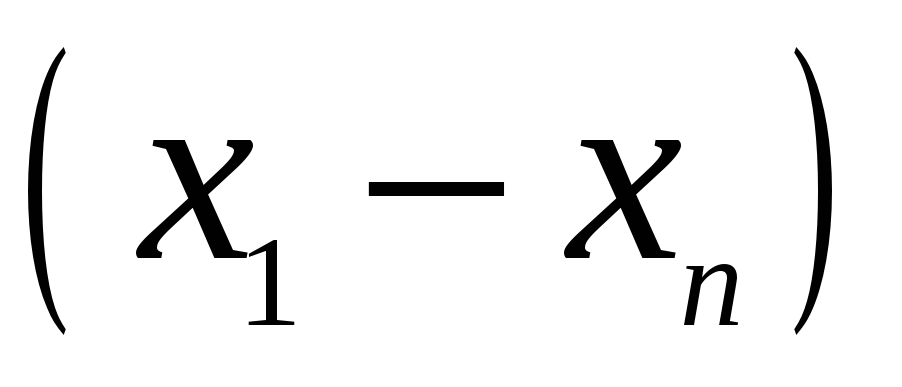
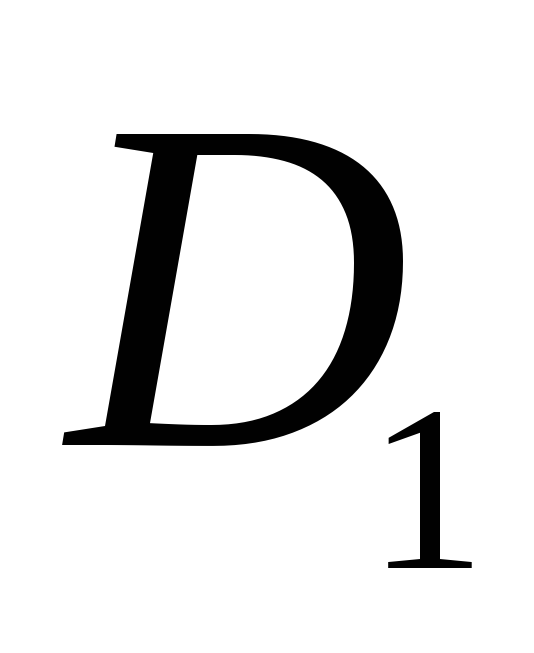
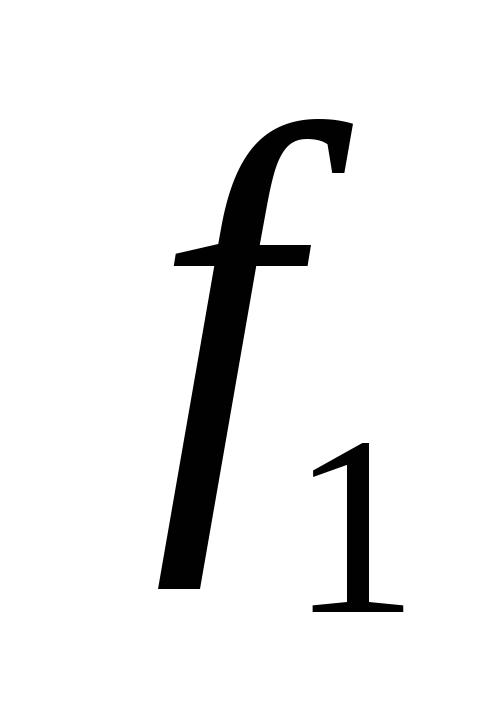
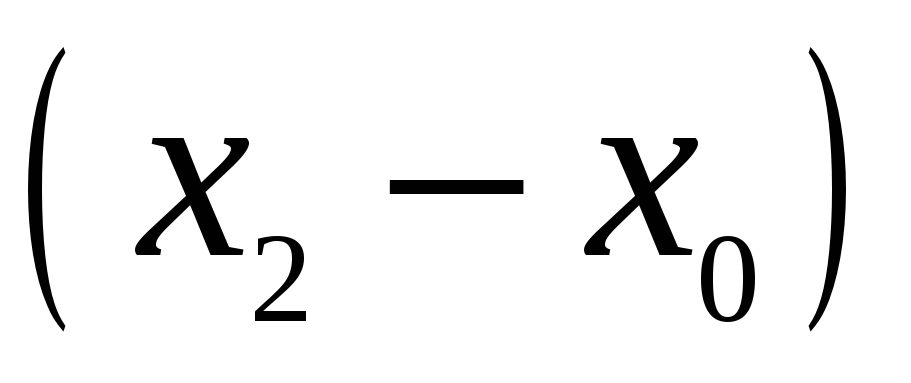
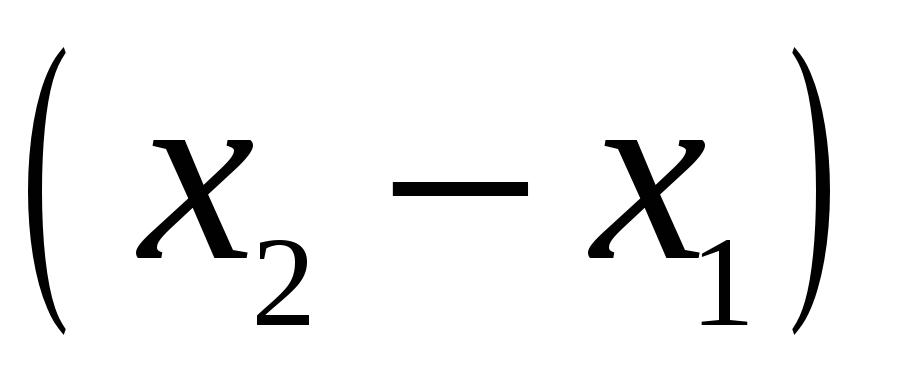
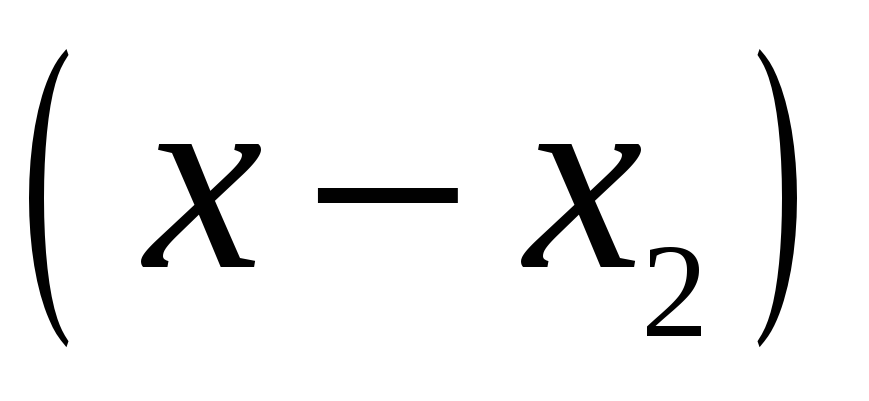
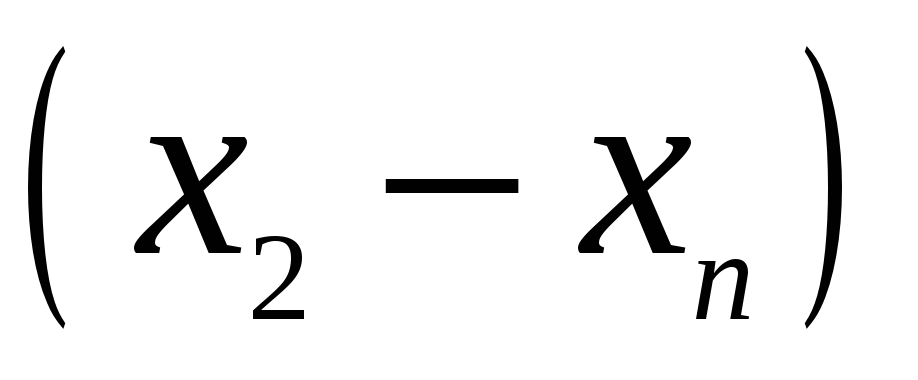
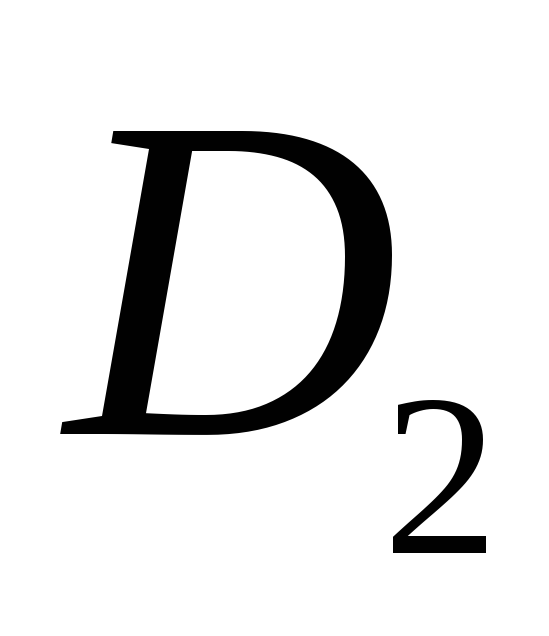
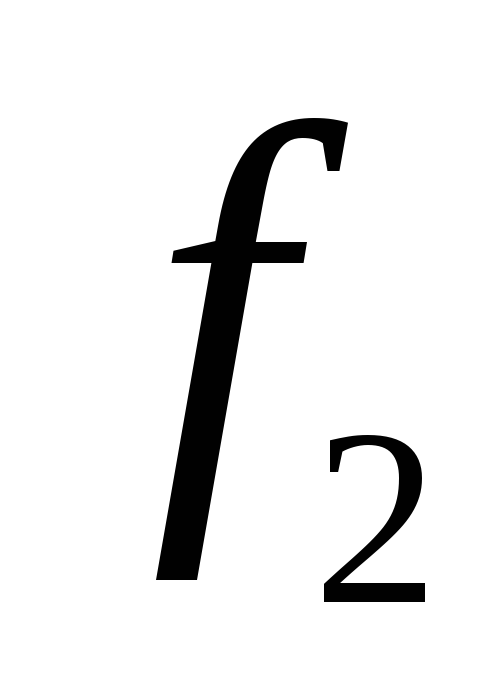
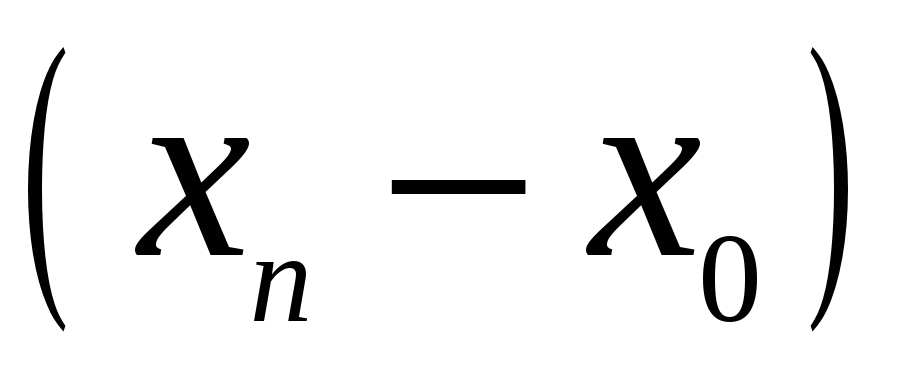
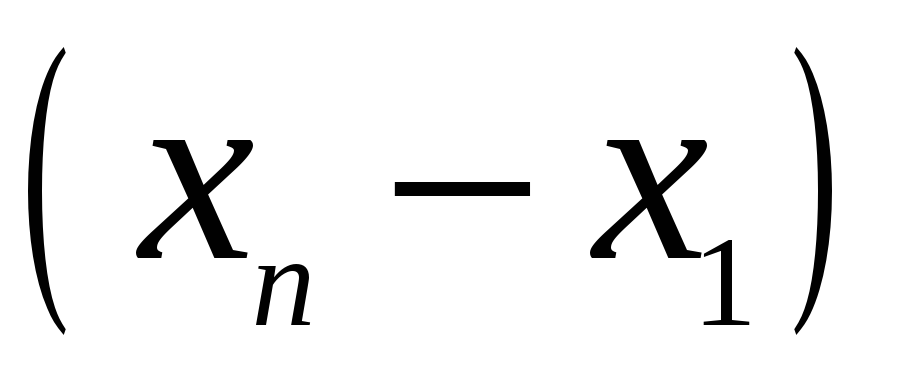
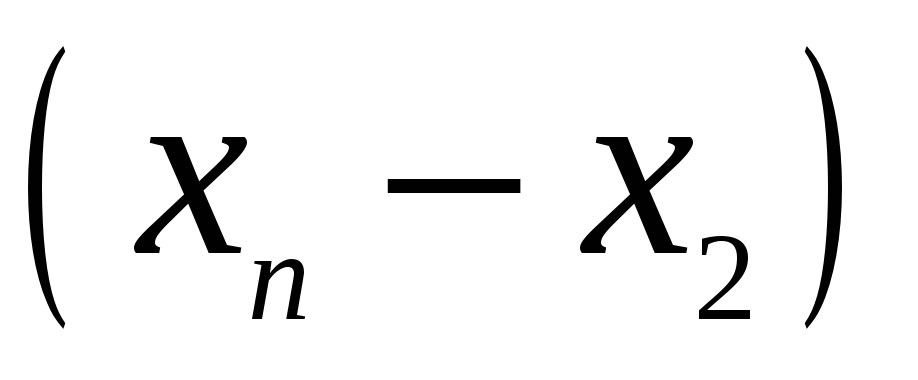
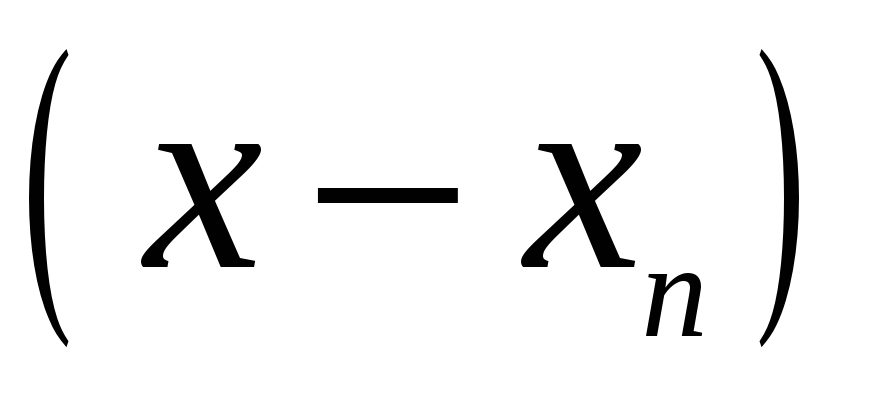
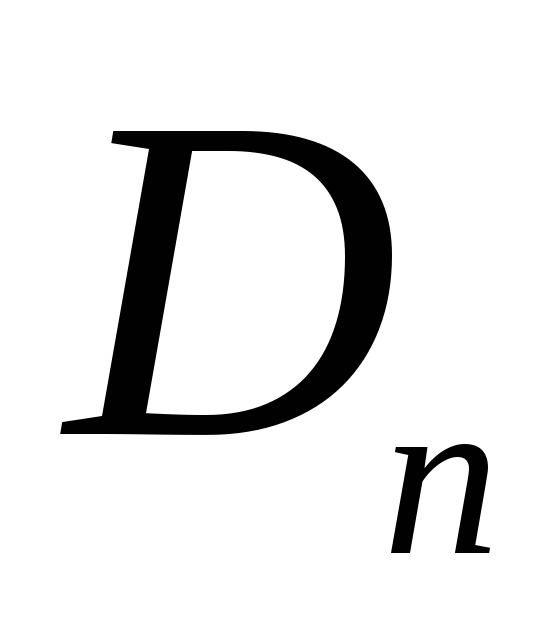
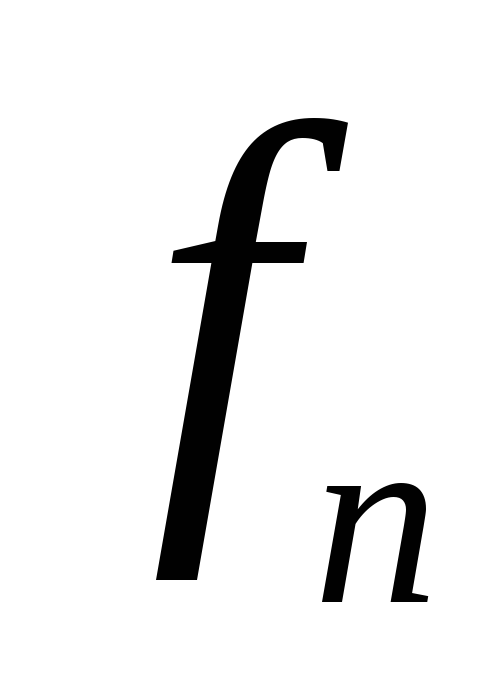
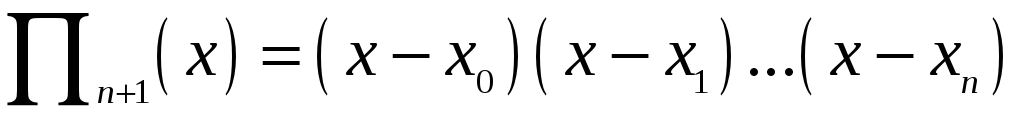
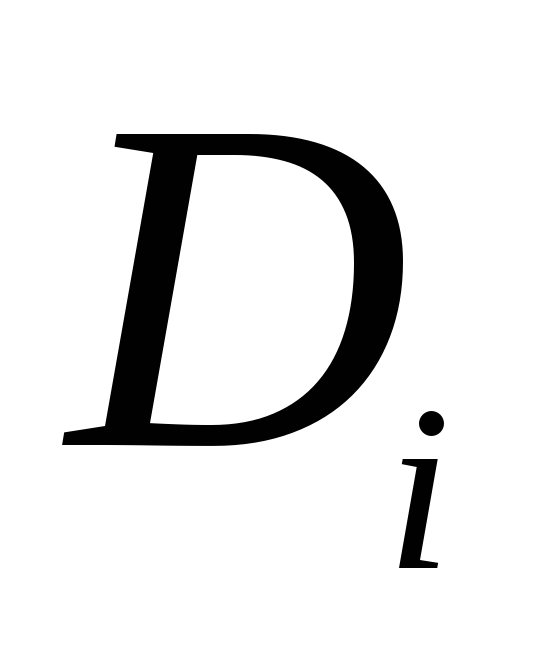
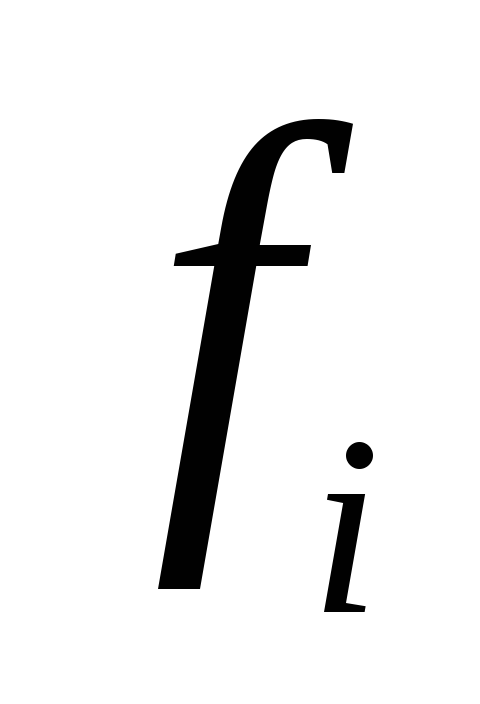
Тут – добуток елементів -го рядка, – добуток елементів головної діагоналі, , .

Тоді многочлен Лагранжа може бути записаним в формі:

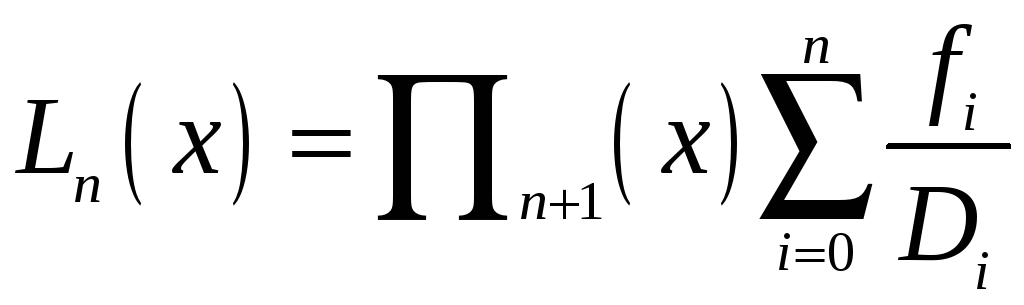. (5)

Приклад 1. Для функції , заданої таблицею своїх значень, побудувати інтерполяційний многочлен 3-го степеня у формі Лагранжа. Обчислити значення функції в точці .

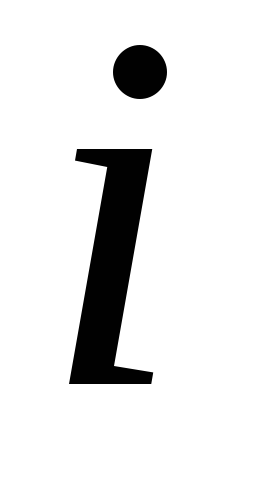
	0	1	2	3
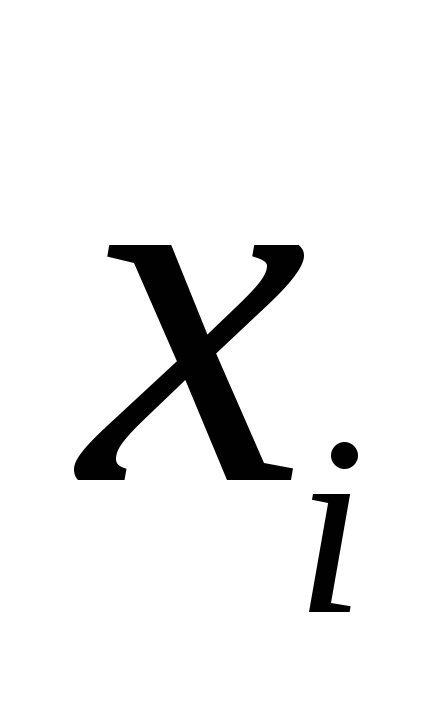
	2	3	4	5
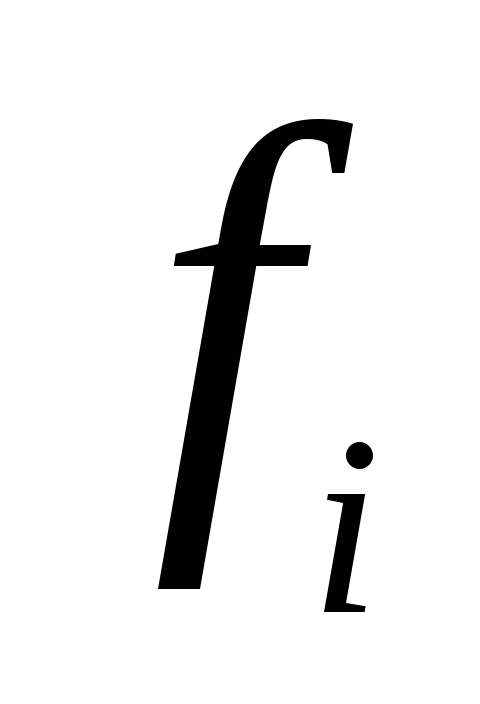
	7	5	8	7

Розв’язання. Побудуємо многочлен Лагранжа. Для цього побудуємо таблицю:

	–1	–2	–3		7
1		–1	–2		5
2	1		–1		8
3	2	1			7

За формулою (5) одержимо:

.
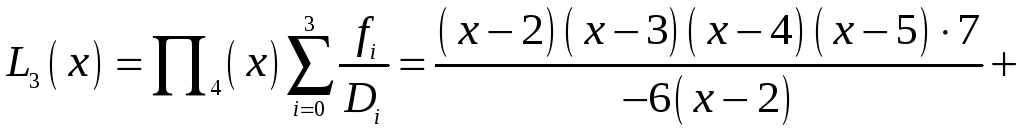
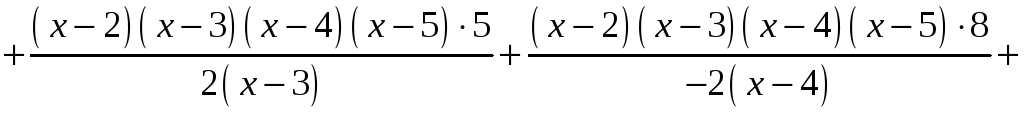
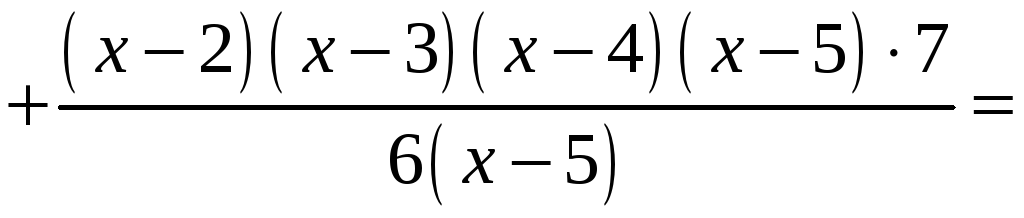
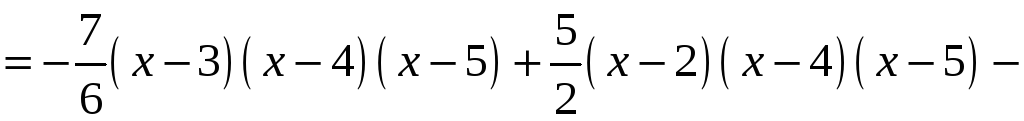
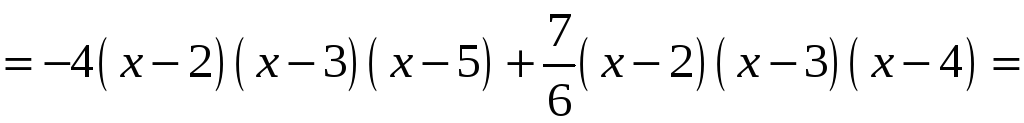
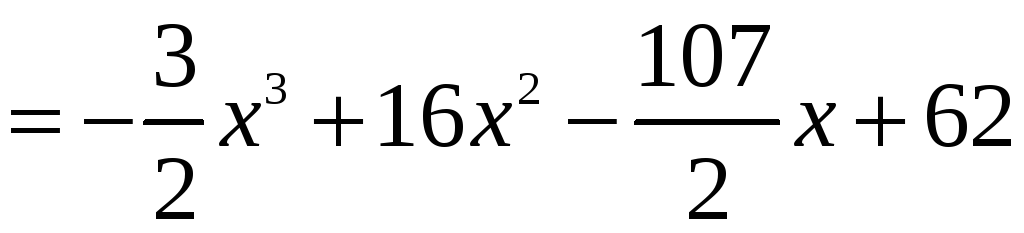