Элементы математической логики

Согласно общим представлениям логика есть область научных знаний, в которой исследуются различные способы суждений и умозаключений и анализируются наиболее общие законы и формы мышления.

Основные определения

 

В математической логикевысказыванием называется повествовательное предложение (утверждение, суждение), которое может быть либо только истинным, либо только ложным. Высказывания будем обозначать буквами латинского алфавита , ,  и т.д., которые назовем логическимипеременными (или пропозициональнымипеременными).

            Пусть  есть множество высказываний, а множество  состоит из двух символов — 0 и 1 (). Установим отображение  так, что каждому истинному высказыванию соответствует  1, а каждому ложному —  0. Символы 1 и 0 назовем значениямиистинности высказываний.

            Из простых высказываний можно с помощью некоторых стандартных связок образовать новые (составные) высказывания. Саму процедуру применения логических связок называют логическими операциями.

Определение 1. Отрицанием высказывания  называется высказывание, соответствующее словам: «не », «неверно, что ». Отрицание обозначается символом  или  ┐ и задается таблицей истинности .

                               

Отметим, что отрицание является унарной логической операцией.

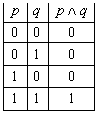
Определение 2.  Конъюнкцией  двух высказываний ,  называют третье высказывание  (читается « и », другое обозначение конъюнкции &), которое истинно тогда и только тогда, когда истинно  и  истинно  .

Определение 3.  Дизъюнкцией двух высказываний ,  называется высказывание  (читается « или »), которое ложно в том и только в том случае, когда ложно  и ложно  

           

                               

Элементы математической логики

Определение 4.  Импликацией  высказываний ,    называется высказывание  («если , то  », «из  следует  »), которое ложно в том и только в том случае, когда   истинно, а   ложно. Высказывание  называютпосылкой, а высказывание  – заключением импликации.

Определение 5.  Эквиваленцией высказываний ,   называется высказывание  («равносильно  »), которое истинно тогда и только тогда, когда значения истинности высказываний  и  совпадают

 

           

Пример 1. Пусть множество  есть подмножество некоторого множества   (). Рассмотрим два высказывания  и  соответственно: «элемент » и «элемент ». Тогда импликации  соответствует следующее высказывание: «если элемент , то элемент ».

При этом трем различным положениям точки, отвечающей элементу  на рис. 1, можно сопоставить три строки таблицы 4, в каждой из которых импликация принимает значение «истина». Действительно, ситуация, когда    и  ,  возможна, этой ситуации соответствует строка  таблицы 4. Точно так же возможны еще два расположения точки   – когда  и  (строка ) и когда и   (строка ). Наконец, в рамках нашего условия () абсолютно невозможно представить ситуацию, когда элемент   и одновременно элемент  (строка ). Таким образом, именно в том случае, когда посылка истинна, а заключение ложно, импликацию  следует признать ложной.

            Еще одно известное обоснование введения импликации с помощью таблицы 4 заключается в том, что импликация вводится таким образом, чтобы два составных высказывания: «из  и   следует » и «из  и   следует » всегда, т.е. при любых значениях истинности высказываний , ,  принимали только значение «истина».

Пример 2. Рассмотрим еще одну импликацию: «если студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту импликацию следует признать ложной лишь в том случае, когда студент сдал на «отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не все экзамены сданы на «отлично» и стипендия получена (например, в силу того, что студент проживает в малообеспеченной семье) либо когда экзамены вообще не сданы и о стипендии не может быть и речи, импликацию можно признать истинной.

             

Определение 6. Выражение называетсялогической формулой (пропозициональнойформулой), если это выражение удовлетворяет следующим условиям:

1)     любая логическая переменная есть формула;

2)     если  и  — формулы, то (┐), (), (), (), () тоже являются формулами;

3)     других формул нет.

Пример 3.  Выражение  ┐ не является формулой, а запись ┐)) представляет собой формулу.  Действительно,  в первом выражении между высказыванием   и высказыванием ┐ вообще нет никакой логической связки, поэтому ┐ не является формулой.