3 Датчик обратной связи

Датчик наклона РФ 711 содержит пузырьковый уровень, подобный ампуле обычного столярного уровня, но более точный. Положение пузырька определяется электроникой путем очень точного измерения его положения относительно проводника, проходящего через уровень. Положение пузырька отслеживается постоянно. Таким образом, блок управления может вычислять угол коррекции.

Выходной сигнал: аналоговый 0…5 В или цифровой RS-232;

Диапазон измеряемой величины -90…+90

Постоянная времени не более 0,1 c;

Погрешность: 10 угл.мин.;

Степень защиты: IP65;

Нелинейность: не более 2%;

Рабочая температура: -40…+50;

Габариты: 80x40x36 мм;

Вес 1,1 кг.

Габаритные и установочные размеры указаны на рисунке 3.

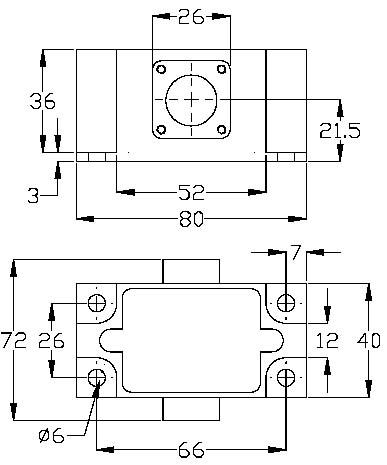
Рисунок 4 – Установочные и габаритные размеры датчика РФ711.

Крепление датчика производится основанием к вертикальной поверхности (отклонение 21), причем верхней стороной считается сторона с маркировкой “U”.

Статической характеристикой данного датчика является зависимость U_вых = f(), где U_вых – выходное напряжение,  - угол наклона датчика.

Uвых, В

, град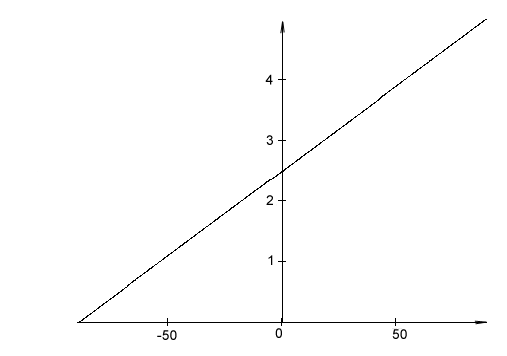

Рисунок 5 – Статическая характеристика.

Зависимость линейная, т.к. чувствительный элемент пропорционально переводит угол наклона прибора в положение пузырька воздуха относительно металлической нити, что изображено на рисунке 2.

Рисунок 6 - Чувствительный элемент датчика наклона. 1 - Корпус уровня; 2 – жидкость; 3 - пузырек газа; 4 – металлическая нить.

Нелинейность возможна при изменении формы корпуса и соответственно профиля дуги, по которой перемещается пузырек.

Передаточная характеристика.

Движение пузырька газа в жидкости, ограниченное круглой или цилиндрической поверхностью, описывается уравнением

, (32)

где  - угол наклона пузырька [рад]; F – внешнее воздействие на уровень, эквивалентное наклону [Н]; m, m₁ – масса воды в уровне и пузырька воздуха, [кг]; e – радиус движения пузырька, [м]; , ₁ – динамические вязкости жидкости и воздуха [Пас];  - кинематическая вязкость жидкости [м²/с];  - плотность жидкости [кг/м³] ; V – объем пузырька воздуха [м³]; g – ускорение свободного падения [м/с²].

Физические размеры уровня датчика РФ711:

Рисунок 7 - Физические размеры чувствительного элемента датчика РФ711: a = 0,025 м, b = 0,004 м, c = 0,002 м.

Учитывая, что

- объем пузырька газа; (33)

- масса пузырька воздуха; (34)

₁ = 1,1 кг/м³ – плотность воздуха; (35)

- масса жидкости; (36)

Примем значения величин m = 0,094 кг, m₁ = 3,610^-6 кг, e = 0,0029 м,  = 1,78 Пас, ₁ =10^-7 Пас,  = 3,5 м²/с,  = 1000 кг/м³ , V = 3,3510^-8 м³, g = 9,8 м/с²;

получим уравнение динамики вида

. (37)

Передаточная функция запишется в виде:

. (38)

Коэффициент при p² на три порядка меньше коэффициента при p, поэтому пренебрежем им. Передаточная функция примет вид

. (39)

Таким образом, геометрические параметры чувствительного элемента датчика угла наклона серии РФ700 удовлетворяют требованиям быстродействия, предъявляемым к данной системе.

4 Исследование устойчивости системы

Структурная схема системы имеет следующий вид:

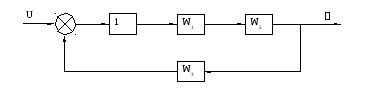
Рисунок 8 – Структурная схема системы регулирования наклона.

Передаточные функции блоков имеют вид

, (40)

, (41)

, (42)

Передаточная функция прямой цепи

; (43)

; (44)

. (45)

Передаточная функция разомкнутой системы

; (46)

. (47)

Передаточная функция замкнутой системы

, (48)

. (49)

Корни характеристического уравнения

(50)

имеют вид -1,0012; -0,8910; -0,1786; -0,0467; -0,0141.

Известно, что при отрицательных вещественных частях характеристического уравнения система устойчива, следовательно, система W_z устойчива.

Годограф Найквиста для разомкнутой системы представлен на рисунке 9.

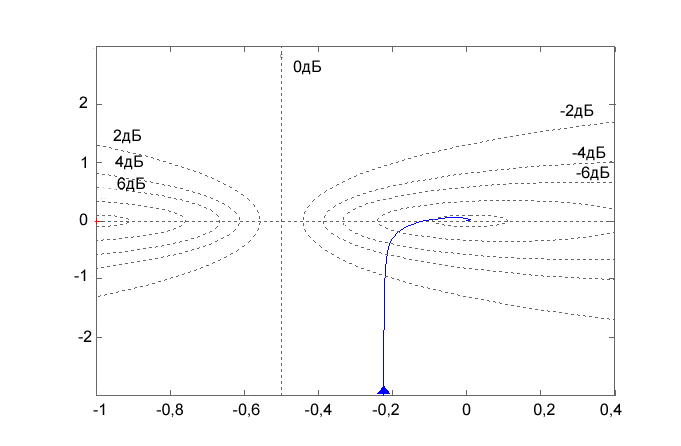
Рисунок 9 – Годограф Найквиста для нескорректированной системы.

Разомкнутая система обладает астатизмом первого порядка, следовательно началом годографа принимается точка (,0). Годограф не охватывает точку (-1;0), следовательно замкнутая система устойчива.

Передаточная функция замкнутой системы с учетом дискретности (T₀=0,05c) и фиксатором нулевого порядка имеет вид

. (51)

Нули характеристического уравнения имеют вид 0,93188; 0,7916; 0,4092; 0,0116; 0,0066.

Нули характеристического уравнения по модулю меньше 1, следовательно замкнутая дискретная система устойчива.

Передаточная функция разомкнутой системы с учетом дискретности и фиксатора нулевого порядка имеет вид

(52)

Проведем  - преобразование, z = (1+) / (1-).

(53)

Сделав замену =0,5T₀s, где T₀ = 0,05 с – период дискретности, получим

, (54)

что соответствует выражению

. (55)

Частоты среза

0,05 Гц = -20 дБ/дек; log(0,05)=-1,3;

6,807 Гц = -20 дБ/дек; log(6,807)=0,833;

15,96 Гц = -20 дБ/дек; log(15,96)=1,2;

40 Гц = -40 дБ/дек; log(40)=1,602;

40,36 Гц = +20 дБ/дек; log(40,36)=1,605;

45,11 Гц = +20 дБ/дек; log(45,11)=1,654;

147 Гц = +40 дБ/дек; log(147)=2,167;

156,5 Гц = +20 дБ/дек; log(156,5)=2,194.

По полученной передаточной функции строим ЛАЧХ системы от псевдочастоты .

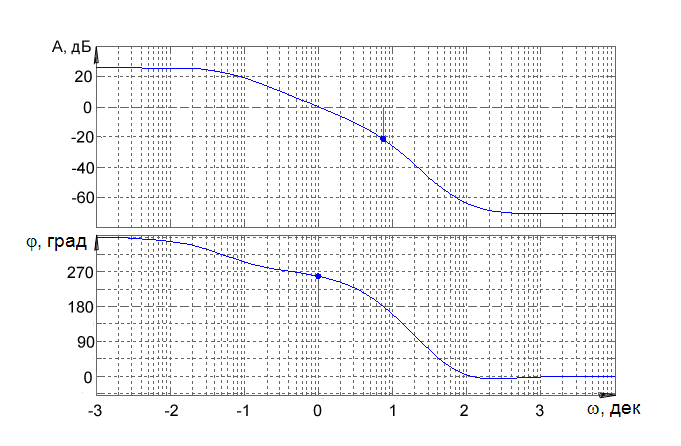
Рисунок 10 – ЛАЧХ и ЛФЧХ нескорректированной системы.

Запасы устойчивости: по амплитуде = 21,5 дБ, по фазе 78,7.

Переходный процесс замкнутой нескорректированной системы с учетом дискретности приведен на рисунке 11.

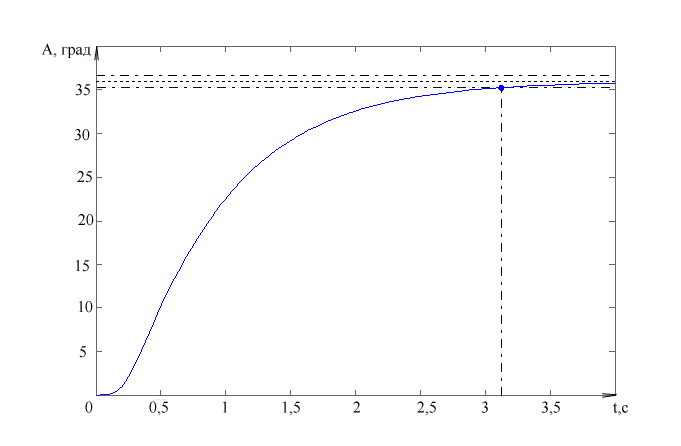
Рисунок 11 – Переходный процесс нескорректированной системы.

Время переходного процесса 3,12с, что не удовлетворяет техническому заданию, следовательно требуется коррекция.