№ документа

Содержание

БИТТУ УИТ –41 2

2

2

3. 2 Определение устойчивости по критерию Шур-Кона 23

3. 3 Билинейное преобразование 24

3. 4 Вывод по исследованию дискретной системы 26

ЗАКЛЮЧЕНИЕ 27

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 28

Введение

Целью данной курсовой работы является исследование характеристик система автоматического регулирования пара в котле. Принципиальная схема системы автоматического регулирования пара в барабане котла представлена на рисунке 1.

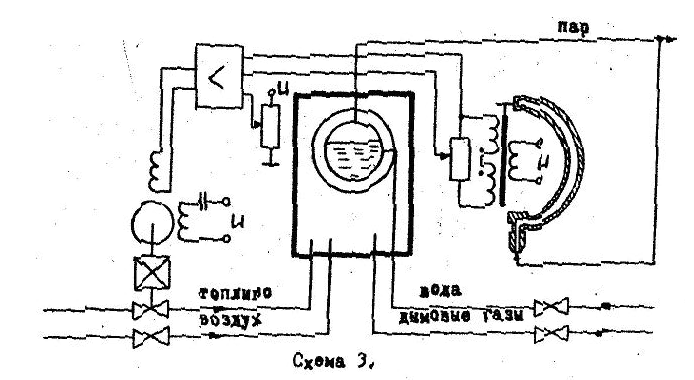
Рисунок 1 - САР давления пара в котле

Объектом управления (ОУ) рассматриваемой САР является котел. Регулируемой величиной является количество подачи топлива , которое сжигается и даёт определенную температуру в котле. При определенной температуре в котле будет определённое давление в барабане котла. Управляющим воздействием на ОУ является открытие вентиля, который регулирует подачу топлива. Основное возмущающее воздействие изменение расхода пара (изменение нагрузки котла).

Система работает следующим образом:

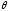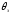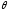в установившемся режиме при равенстве давления в котле заданной напряжение . При отклонении давления пара в котле от заданной, на входе ДУ появляется разность напряжений, отличная от нуля, что приводит к появлению потенциала на его выходе. Начинает вращаться двигатель, отклоняя через редуктор фрамуги на угол , до того момента, пока разность напряжений не станет равна нулю.

1. ПРЕОБРАЗОВАНИЕ ЛИНЕЙНОЙ СИСТЕМЫ

1. 1. Построение функциональной схемы и преобразование её в структурную.

P_з

U_з

U_y

φ_дв

φ_о

Q

P

-

P_д

З – задающее устройство;

У – усилитель;

Дв – двигатель;

Р – редуктор;

К – котел.

Рисунок 2 - Функциональная схема САР давления пара в котле

Преобразуем функциональную схему в структурную с передаточными функциями.

P_з

U_з

U_y

φ_дв

φ_о

Q

P_д

P

-

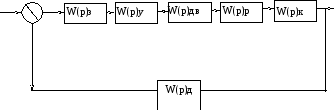
Рис. 3 Структурная схема САР давления пара в котле

1. 2. Нахождение передаточной функции системы

- передаточная функция задатчика

- передаточная функция усилителя

- передаточная функция двигателя

- передаточная функция редуктора

- передаточная функция котла

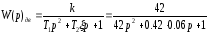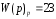- передаточная функция двигателя

Найдем общую передаточную функцию системы.

Звенья соединены встречно-параллельно, поэтому запишем общую передаточную функцию системы:

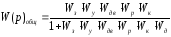
Воспользовавшись математическим редактором Mathcad 11, получим передаточную функцию системы с численными значениями.

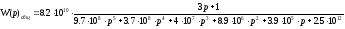
Вынесем за скобки 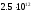, получим:

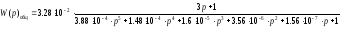
Найдем корни характеристического уравнения, для этого приравняем знаменатель к нулю.

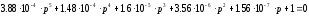
Система является неустойчивой, так как корни характеристического уравнения есть и с положительным и с отрицательным знаком. Согласно критерию устойчивости Ляпунова корни должны лежать в левой полуплоскости комплексной плоскости, а для этого они должны иметь отрицательную вещественную часть комплексного числа.

Воспользовавшись критерием устойчивости Евсюкова можно определить коэффициент, который влияет на устойчивость системы, и изменить его, добившись устойчивости системы.

Определим через k величину возрастания коэффициентов характеристического уравнения:

; ; ; ;

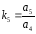
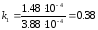
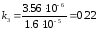
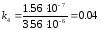
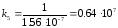
Для устойчивости системы необходимо чтобы выполнялось условие:

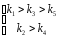
Данное условие не выполняется. Чтобы система стала устойчивой необходимо уменьшить коэффициент k₅, который равен k₅=a₅/ a₄ . Для этого уменьшим коэффициент a₅, и примем его равным 10^-8.

Получим характеристическое уравнение вида:

Найдем его корни с помощью Mathcad 11.

Система является устойчивой, так как все корни характеристического уравнения имеют отрицательную вещественную часть комплексного числа. Следовательно, все корни располагаются в левой полуплоскости комплексной плоскости. Условие устойчивости Ляпунова выполняется.

Получим передаточную функцию:

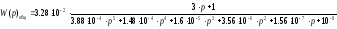
Приведем передаточную функцию к стандартной форме, для этого вынесем 10^-8 за скобку.

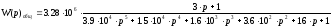
1. 3. Проверка устойчивости по критерию Гурвица

Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны.

Составим главный определитель Гурвица по коэффициентам характеристического уравнения

∆=

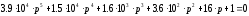
Вычислим все миноры с помощью Mathcad 11:

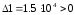
∆2=

∆3=

∆4=

∆5=

Система является устойчивой, так как все миноры определителя Гурвица больше нуля. Необходимое и достаточное условие выполняется.

1. 4. Проверка устойчивости по критерию Михайлова

Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения, последовательно проходя эти квадранты.

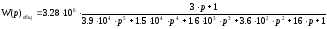
Введем замену p=jω.

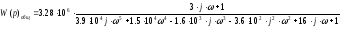Запишем характеристическое уравнение системы:

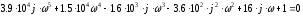
Выделим вещественную и мнимую части:

Определим особые точки. Это точки пересечения годографа с осями координат. Для системы пятого порядка таких точек 5.

Определим значение частот, при которых вещественная часть характеристического вектора равна нулю, воспользовавшись Mathcad 11. Для построения годографа берем только положительные частоты.

Определим значение мнимой части в этих точках:

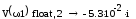
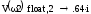
Определим значение частот, при которых мнимая часть характеристического вектора равна нулю.

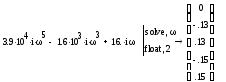
Определим значение вещественной части в этих точках:

Результат вычисления особых точек сведем в таблицу 1.

Таблицу 1

№	1	2	3	4	5
ω	0	5.7*10-2	0.13	0.14	0.15
U(ω)	1	0	-0.8	0	0.49
V(ω)	0	0.64j	0	-5.3*10-2j	0

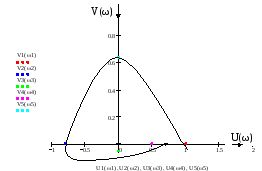
Рисунок 4 – Годограф Михайлова

Система является устойчивой, так как условие устойчивости выполняется.