5 Построение лачх системы и ее анализ

Для того чтобы построить ЛАЧХ системы необходимо найти передаточную функцию разомкнутой системы.

(68)

(69)

Передаточная функция разомкнутой системы имеет вид передаточной функции апериодического звена, где k=5.18; Т=0.04.

Логарифмическая характеристика апериодического звена:

(70)

(71)

Выполним анализ выражения (71) для следующих диапазонов частот:

пусть w< или wT<1, тогда ;

пусть w> или wT>1, тогда

Таким образом, на участке w< логарифмическая характеристика проходит горизонтально и наклона не имеет, а на участке w > 1/Т логарифмическая характеристика будет иметь наклон (-20)дБ/дек.

w= - частота сопряжения, при Т=0.04, w=25

ЛАЧХ проектируемой системы будет иметь вид соответствующий рисунку 11.

L(w)

20

10

0

-10

-20

10

w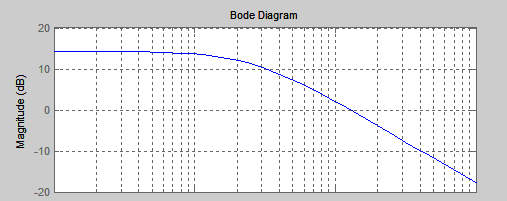

10

10

10

Рисунок 11 - ЛАЧХ разомкнутой системы регулирования мышеловкой

Построим ЛФЧХ системы.

(72)

Если w=0, тогда =0;

если w=, тогда;

еслиw,тогда. .

ЛФЧХ проектируемой системы будет иметь вид, соответствующий рисунку 12.

0

w

-90

-45

10

10

10

10

Рисунок 12 - ЛФЧХ разомкнутой системы регулирования мышеловкой

Выполним анализ ЛАЧХ и ЛФЧХ и определим запасы устойчивости по амплитуде и фазе.

По фазе запас устойчивости определяется превышением (w) над осью 180 на частоте пересечения L(w) с осью lgw:

(73)

По амплитуде запас устойчивости определяется превышением L(w) над осью lgw на частоте пересечения (w) с осью 180. Так как (w) не достигает 180, находясь выше этого значения, то запас устойчивости по амплитуде L_з = .

Низкочастотная асимптота имеет наклон (0 дБ/дек) и лежит в области частот от 0 до 25 Гц.

Среднечастотная асимптота имеет наклон (-20 дБ/дек) и лежит в области частот от 25 до Гц.

6 ПОСТРОЕНИЕ ЖЛАЧХ СИСТЕМЫ

ЖЛАЧХ для систем строится, используя номограмму Солодовникова. По номограмме Солодовникова определяем частоту среза по заданному перерегулированию и времени регулирования системы:

σ_m = 20% (74)

t_p = 0.5 c (75)

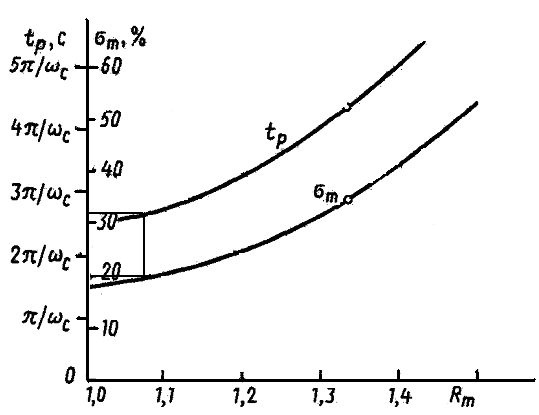
Рисунок 13 - Номограмма Солодовникова

Определение частоты среза поипо формуле:

, (76)

где k определяется по номограмме Солодовникова (k=2.6).

рад/с (77)

Среднечастотная асимптота ЖЛАЧХ проводится через точку w_c с наклоном (-20 дБ/дек), так как при большем наклоне трудно обеспечить необходимый запас устойчивости и допустимое перерегулирование. Основные динамические свойства связаны с длиной этой асимптоты. Для ее определения примем показатель колебательности М = 2 , тогда:

(78)

(79)

Прямые инаносятся на график параллельно осиlgw. Они пересекают L_ж в точках (а) и (б). Среднечастотная асимптота L_ж проходит из точки (а) под наклоном (-20 дБ/дек).

Низкочастотная асимптота L_ж проходит параллельно асимптоте L. При этом получаем новый коэффициент передачи системы: 20lgk_ж = 6.02; k_ж = 2

Передаточная функция ЖЛАЧХ.

W_ж= (80)

где k_ж = 2, Т_ж=0.1 сек.

Рисунок 14 – ЛАЧХ и ЖЛАЧХ системы регулирования мышеловкой

Для того чтобы найти запасы устойчивости по фазе и амплитуде необходимо построить ЖЛФЧХ системы.

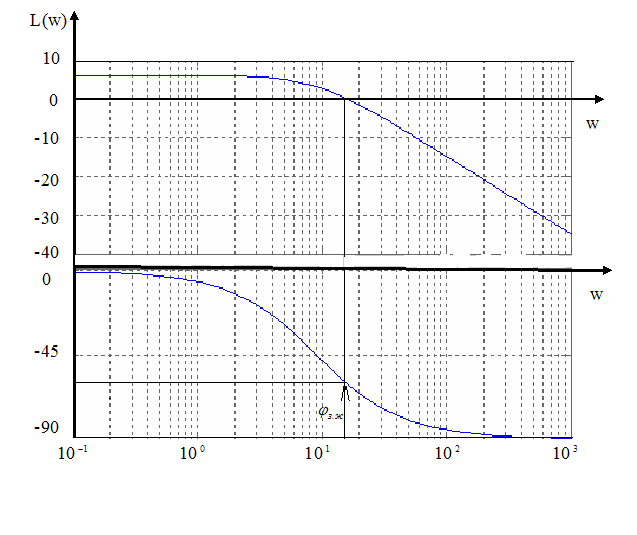
Рисунок 15 – ЖЛАЧХ и ЖЛФЧХ системы регулирования мышеловкой

По фазе запас устойчивости определяется превышением (w) над осью 180 на частоте пересечения L(w) с осью lgw:

. (81)

По амплитуде запас устойчивости определяется превышением L(w) над осью lgw на частоте пересечения (w) с осью 180. Так как (w) не достигает 180, находясь выше этого значения, то запас устойчивости по амплитуде L_з.ж = .

7 ПОСТРОЕНИЕ ЛАЧХ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА РАСЧЕТ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

Коррекция динамических свойств САР осуществляется для выполнения требований по точности, устойчивости и качеству переходных процессов.

Коррекция применяется также как средство обеспечения устойчивости неустойчивой системы или расширения области устойчивости, а также повышения качества переходного процесса.

Осуществляется коррекция с помощью введения в систему специальных корректирующих звеньев с особо подобранной передаточной функцией. Принципиально корректирующие звенья могут включаться либо последовательно с основными звеньями САУ, либо параллельно им (существуют и комбинированные способы включения).

Наиболее удобно использовать корректирующее устройство последовательного типа, поскольку оно обеспечивает наиболее простую схему включения, не требует сложных элементов для согласования, передает значительные величины управляющих сигналов (тока, напряжения).

К достоинствам последовательной коррекции можно отнести:

- ускорение переходного процесса;

- снижение установившейся ошибки;

- простоту включения элементов коррекции.

К недостаткам можно отнести:

- увеличение чувствительности к помехам;

- необходимость согласования сопротивления корректирующих элементов с входным и выходным сопротивлением элементов системы, к которым они подключаются;

- снижение величины основного сигнала.

Рассмотрим коррекцию заданной системы с помощью последовательного корректирующего устройства.

Передаточная функция желаемой системы

, (82)

где W – передаточная функция разомкнутой САУМ; W_к – передаточная функция корректирующего устройства.

Логарифмируя выражение (82), получим:

(83)

Логарифмическая характеристика корректирующего устройства

, (84)

где L_ж – логарифмическая характеристика желаемой системы; L – логарифмическая характеристика САУМ.

Вычитание производится графически. По построенной ЛАЧХ корректирующего устройства можно выполнить переход к передаточной функции W_к. Для этого для каждой точки излома ЛАЧХ корректирующего устройства определяются частоты сопряжения, соответствующие постоянным времени. Участку 1-2 L_к соответствует апериодическому звену с передаточной функцией . На участке 2 -наклон уменьшается на 20 дБ, значит, появляется влияние форсирующего звена (Т₂р+1).

Таким образом, передаточная функция корректирующего устройства

, (85)

где k= 0.386; Т₁ = 0,11 с; Т₂ = 0,04 с.

(86)

Рисунок 16 – Построение ЛАЧХ КУ

По виду ЛАЧХ КУ и по найденной W_к подбирается соответствующее корректирующее устройство, представленное на рисунке 17.

Рисунок 17 - Последовательное корректирующее устройство

Используя формулы (87) - (90), рассчитаем параметры корректирующего устройства.

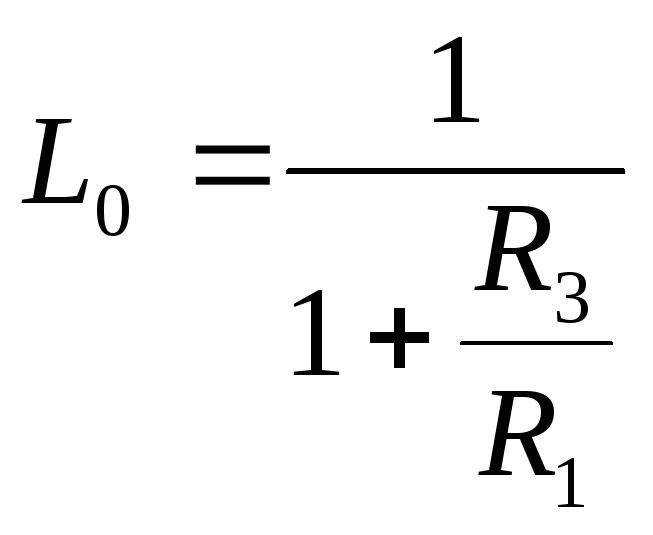(87)

(88)

(89)

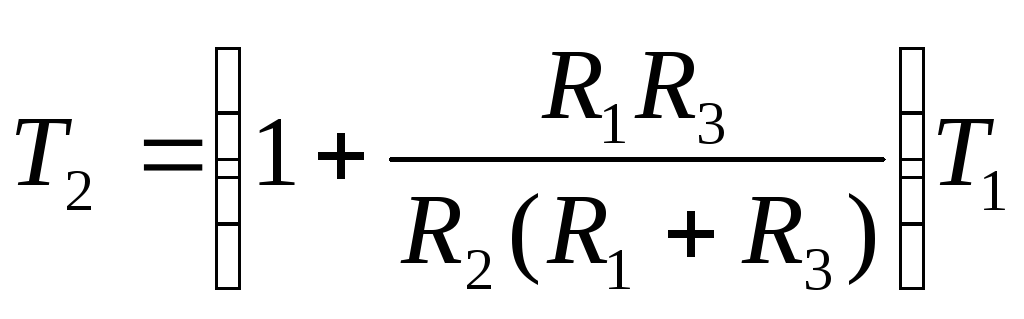(90)

По виду передаточной функции определяем: T₁ =0,04, T₂ =0,11, L_ = 0.143, L₀ = k = =0.386.

Выбирая = 10 мкФ, рассчитаем, выразив его из формулы (90):

(91)

к Ом (92)

Рассчитаем отношение , выразив его из формулы (87):

(93)

Рассчитаем , выразив его из формулы (88):

(94)

к Ом (95)

Из формулы (93) определим :

к Ом (96)

Выбранное корректирующее устройство поместим в САУМ, наиболее предпочтительным вариантом включения электрического корректирующего устройства является участок перед двигателем, так как наибольшую ошибку в работу системы вносит датчик угла поворота.

Рисунок 18 – САУМ с включенным в нее корректирующим устройством

Передаточная функция скорректированной системы:

(97)

Построим график переходного процесса скорректированной системы (рисунок 19).

(98)

Рисунок 19 – Переходный процесс скорректированной САУМ

По графику переходного процесса (рисунок 19) определим показатели качества САУМ:

- перерегулирование:  = ;

- время нарастания: t_н = 1 сек;

- время регулирования: t_р = 0.5 сек.

Скорректированная система удовлетворяет требованиям, предъявляемым к проектироваемой системе в техническом задании.

ЗАКЛЮЧЕНИЕ

В рамках заданной курсовой работы разработана система автоматического управления мышеловкой, которая соответствует требованиям технического задания.

В процессе выполнения курсовой работы были построены логарифмические амплитудно и фазочастотные характеристики, желаемые логарифмические амплитудно и фазочастотные характеристики, были определены запасы устойчивости по данным характеристикам а также с помощью методов синтеза было разработано корректирующее устройство, приводящее параметры системы к величинам из технического задания. В качестве корректирующего устройства используется RC-цепочка.

Таким образом, курс ЛСА был приложен к практической задаче, и она была разрешена в соответствии с теорией.