4 Расчет устойчивости системы

4.1 Передаточная функция системы

Структурная схема системы автоматического управления движением век терминатора имеет вид, показанный на рисунке 5.

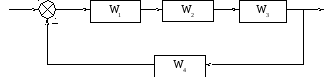
W₁ – передаточная функция микропроцессора; W₂ – передаточная функция гидроцилиндра; W₃ – передаточная функция объекта управления;

W₄ – передаточная функция магнитожидкостного датчика угла.

Рисунок 5 – Структурная схема замкнутой системы автоматического

управления движением век терминатора

Передаточные функции блоков имеют вид:

;

;

;

.

Рассчитаем передаточную функцию замкнутой системы.

.

Упростим передаточную функцию с помощью программы Mathcad:

.

4.2 Оценка устойчивости аналоговой системы

Оценку устойчивости проведем по критерию устойчивости Гурвица. Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительными. Характеристическое уравнение системы:

Все коэффициенты характеристического уравнения положительные,

значит необходимое условие устойчивости выполняется.

По коэффициентам характеристического уравнения составляется определитель Гурвица. Для этого по главной диагонали определителя выписываются все коэффициенты характеристического уравнения, начиная со второго, затем вверх записываются коэффициенты с возрастающим индексом, а вниз с убывающим индексом.

Составленный определитель называется главным определителем Гурвица, он имеет порядок, совпадающий с порядком характеристического уравнения. Из главного определителя составляются частные определители первого, второго, третьего и т.д. порядков их образования из главного определителя.

Вычисляя главный определитель и частные определители, Гурвиц установил, для того, чтобы система была устойчива необходимо и достаточно, чтобы все определители были положительны. Если хотя бы один определитель отрицательный, то система неустойчива.

Порядок характеристического уравнения: n = 3.

Коэффициенты характеристического уравнения:

a₀ = 0.00002, a₁ = 0.0013, a₂ = 0.035, a₃ = 1.

Определитель Гурвица для заданной системы будет иметь вид:

.

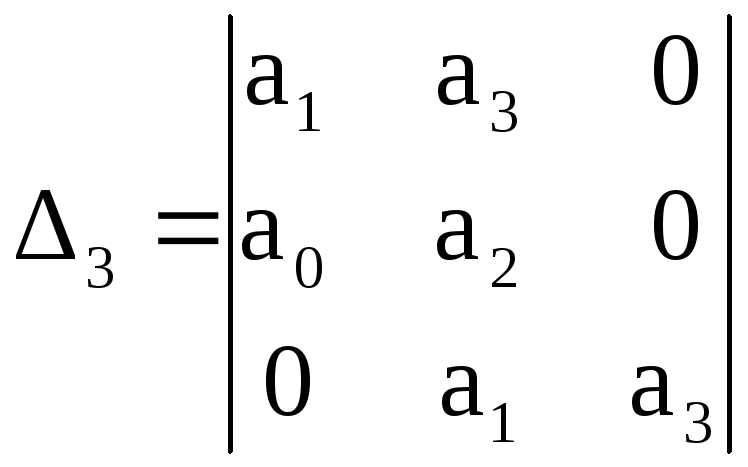Подставим в общую формулу для определителя Гурвица значения коэф-

фициентов характеристического уравнения, получим:

.

Определим значения миноров определителя Гурвица.

;

;

.

Вывод: все коэффициенты характеристического уравнения положительные, значит, необходимое условие устойчивости выполняется. Кроме того, все миноры определителя Гурвица положительны, значит, вещественная часть корней характеристического уравнения отрицательна, и, согласно теореме Ляпунова, система устойчива.

4.3 Расчет показателей качества системы

Переходная функция – это реакция системы на ступенчатое входное воздействие. Она определяет динамические свойства и качественные показатели САУ.

Для того чтобы построить переходный процесс, используем обратное преобразование Лапласа от функции вида .

Следовательно, переходная функция:

Для построения переходного процесса используем программу MathCAD.

h(t)

20

16.67

13.33

10

6.67

0

0.033

0.067

0.1

0.13

0.17

0.2

3.33

0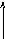

t, с

Рисунок 6 – График переходного процесса

Анализируя график (рисунок 6), можно судить о том, что полученная линейная система устойчива. По переходной функции определим характеристики:

– установившееся значение переходного процесса h_уст = 18.03;

– максимальное значение переходного процесса: h_max = 19.39;

– время первого согласования t₁ = 0.067 c;

– время регулирования t_р = 0.046 c;

– перерегулирование:

.

Построим амплитудно-частотную характеристику системы.

Амплитудно-частотная характеристика строится для того, чтобы определить косвенные оценки качества системы.

Для того, чтобы определить амплитудно-частотную характеристику системы, необходимо в передаточной функции W_зам(p) р заменить на jω:

.

Построим амплитудно-частотную характеристику системы, используя

прикладную программу MathCAD.

.

На рисунке 7 представлен график амплитудно-частотной характеристики.

Определим по графику, представленному на рисунке 7, косвенные оценки качества системы:

– амплитуда при нулевой частоте A(0) = 17.9;

– максимальная амплитуда А_max = 18.83;

– резонансная частота _p = 61 Гц;

– полоса пропускания (промежуток частот, при котором значения амплитуды больше ) 0<<152.44 Гц;

– показатель колебательности:

20

.

А(ω)

166.67

333.33

500

666.67

833.33

16.67

13.33

10

6.67

3.33

0

0

1000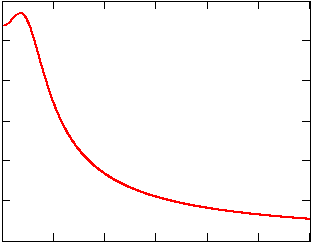

ω, Гц

Рисунок 7 – Амплитудно-частотная характеристика системы

По характеру переходного процесса можно сделать вывод, что исследуемая система устойчивая, т.к. через определенное время регулирования t_р = 0.046 c система приходит в установившееся состояние. Величина перерегулирования для данной системы σ = 7.5 %, что свидетельствует о наличии ошибки в работе системы и не точности передаваемого сигнала. Быстродействие системы, определяемое временем регулирования t_р, соответствует заданному в техническом задании (t_р = 0.5 с).