4 Расчет устойчивости системы

Рисунок 3 - Структурная схема автоматической системы контроля

твердой фазы в жидких дисперсных системах

Устойчивость системы будем проводить методом Ляпунова. Для этого необходимо найти характеристическое уравнение. Сначала найдем передаточную функцию разомкнутой цепи:

Теперь найдем передаточную функцию замкнутой системы

(17)

Характеристическое уравнение системы примет вид:

0,0095s⁴+11,925s³+24,32s²+1,14s+0,28=0

Корни характеристического уравнения:

s₁=-123,45; s₂=-2,03; s₃=-20,9-0,106j; s₄=20,9+0,106j

Отсюда можно сделать вывод, что система является устойчивой, так как корни характеристического уравнения находятся в левой полуплоскости.

Теперь построим переходный процесс. Для этого проведем обратное преобразование Лапласа выражения (17), получим:

h(t)=1-8,9exp(-1253,22t)-1,5exp(-2t)-0,99exp(-0,02t)cos(0,1t)

Рисунок 4 - Переходный процесс системы без учета дискретности

По рисунку 4 определим оценки качества системы.

1. Важнейшим параметром является время регулирования t_р. Под ним понимают время, в течение, которого переходная функцияh(t) достигает установившегося значенияh_устс заданной точностью ∆, где ∆ обычно выбирают 5% отh_уст. В нашем случаеt_р=130 с.

2. Перерегулирование  максимальной динамической ошибкой и определяет максимальное отклонение регулируемой величины от установившегося значения

=55%

3. Время нарастания t_н=15 с. Под ним понимают время за которое переходная функция впервые достигает установившегося значения.

4. Число колебаний

n=2

5. Максимальное значение переходного процесса

h_мах=1,55

6. Минимальное значение переходного процесса

h_min=0,7

7. Период колебания

Т=60 с

8. Частота колебаний

ω=0,105 1/с

9. Декремент затухания к=1,83. Чем больше декремент затухания, тем быстрее затухает процесс и тем качественнее управление

Так как система имеет микропроцессор, то необходимо проводить z преобразование и также исследовать ее на устойчивость. Для этого зададим период дискретности, но так как микропроцессор может обрабатывать информации намного больше, чем нам надо, то поэтому мы не можем взять период дискретности всей ЦВМ. По этой причине мы берем период дискретности который нужен для нормальной работы системы: Т₀=0,01 К=1,166

Проведем z преобразование для АЦП, ЦАП, ЦВМ.

W_АЦП(Z)=КТ₀=11,66

W_ЦАП(Z)=

W_ЦВМ(Z)==

Проведем z преобразование передаточной функции бака со взвесью.

Проведем z преобразование передаточной функции электродвигателя. Разложим передаточную функцию (2) на элементарные дроби методом неопределенных коэффициентов

0,019As²+23,812As+A+Bs²+Cs=0,8

Найдем передаточную функцию разомкнутой системы

Найдем передаточную функцию замкнутой системы

Устойчивость системы будем проводить методом Ляпунова. Для этого необходимо найти характеристическое уравнение. Характеристическое уравнение будет иметь вид:

Корни характеристического уравнения

; ;

Система является устойчивой, потому что корни находятся в левой полуплоскости.

Для того чтобы построить переходный процесс, необходимо провести

замену 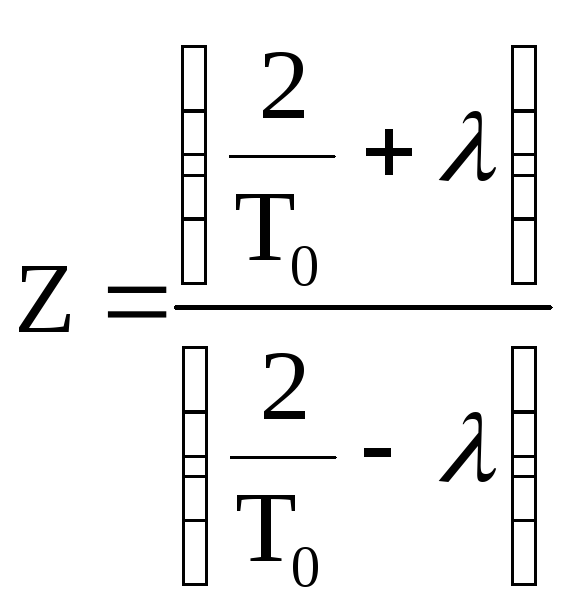, тогда получим

(18)

Произведем обратное преобразование Лапласа

h(t)=0,086+0,14exp(-376,2t)+0,288exp(629,7t)-6,4exp(-201,35t)

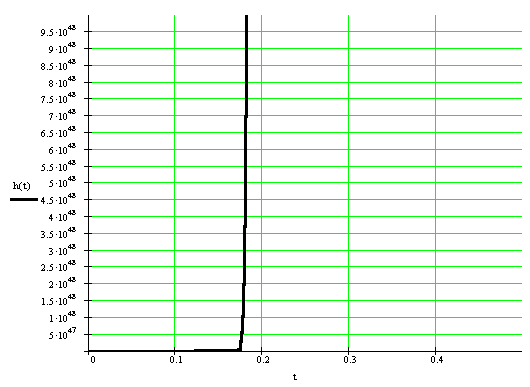
Рисунок 5 Переходный процесс системы с учетом дискретности

Система с учетом дискретности устраивает те параметры, которые были заданы в расширенном техническом задании, то есть время регулирования этой системы меньше, чем у той величины которая была задана.

5 ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДО-

ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ И ЕЕ АНАЛИЗ

При помощи математических вычислений передаточную функцию (18) можно привести к виду:

Найдем частоты излома логарифмической амплитудо-частотной характеристики системы

₁=0,0012; ₂=0,0041; ₃=0,0059; ₄=0,0094; ₅=0,463; ₆=0,5

Теперь построим логарифмическую амплитудо-частотную характеристику

Рисунок 6 - Логарифмическая амплитудо-частотная характеристика

системы

Для определения запасов устойчивости необходимо построить фазо-частотную характеристику

Рисунок 7 - Фазо-частотная характеристика системы

Запас устойчивости по амплитуде достаточен, так как ФЧХ не пересекает угол /2 и уходит в бесконечность. Запас устойчивости по фазе =15⁰ и является достаточным для этой системы.

6 ПОСТРОЕНИЕ ЖЕЛАЕМОЙ ЛОГАРИФМИЧЕСКОЙ

АМПЛИТУДО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ,

ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДО-ЧАСТОТНОЙ

ХАРАКТЕРИСТИКИ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

Строить ЖЛАЧХ будем методом запретной зоны. Построение ЖЛАЧХ начинается с низкочастотной области из условия требуемой точности работы определяемое положением контрольной точки. Низкочастотная часть ЖЛАЧХ должна проходить не ниже контрольной точки или так чтобы не заходить в запретную зону. Перед построением необходимо определить некоторые параметры: М=А_max/A(0)=2; _ср=b/t_р=9.

Так как у нас в системе есть компьютер и большинство электрических связей, то максимально допустимая ошибка 0,005. Максимальная скорость изменения сигнала, так как скорость прохождения света через бак со взвесью небольшая. Максимальное ускорение изменения сигнала будет еще меньше потому, что свет проходя сквозь бак со взвесью теряет свою скорость.

(19)

А=(20)

Вычислив значение по формуле (20) подставим его в следующую формулу

(21)

Получив значения вычисленные по формулам (19) и (21) можно найти положение контрольной точки А(_к; 20lgА₁). Подставив значения получим точку с координатами А(0,01;46)

Протяженность находится по формуле

Граничные частоты ;

Теперь построим ЖЛАЧХ.

Рисунок 8 - Желательная амплитудо-частотная характеристика системы

Так как ЛАЧХ лежит в запретной зоне, поэтому нам необходимо поднять ЛАЧХ и тогда она будет проходить по ЖЛАЧХ. Теперь можно построить ЛАЧХ корректирующего устройства. Она находится как разность ЖЛАЧХ и ЛАЧХ и выглядит следующим образом.

Рисунок 9 - Логарифмическая амплитудо-частотная характеристика

корректирующего устройства