Гармоническая линеаризация нелинейности. Расчёт знсау частотно-амплитудным методом

Рассмотрим метод гармонической линеаризации. Пусть на вход нелинейного элемента подан гармонический сигнал: (6.1). На выходе получим сигнал(6.2), который можно разложить в ряд Фурье:

Где – коэффициенты ряда Фурье:

Где .

Примем:

Тогда уравнение (6.2) примет следующий вид:

В области изображений:

Передаточная функция гармонически линеаризованного нелинейного элемента:

Частотная передаточная функция ГЛНЭ:

Коэффициенты для нелинейности:

(т.к. нелинейность однозначная).

Определим наличие периодического режима частотно-амплитудным методом.

1. Гармоническая линеаризация нелинейного элемента:

2. Условие существования периодического режима:

(6.3)

Где – АФХ разомкнутой гармонически линеаризованной системы (РГЛС), т.е. используется критерий Найквиста: в замкнутой ГЛНС будет периодический режим, если АФХ РГЛС проходит через точку с координатами.

Уравнение (6.3) в иной форме:

С помощью программы MathCadстроим АФХ линейной части и инверсную АФХ нелинейного элемента.

Значение амплитуды от 0 до 300.

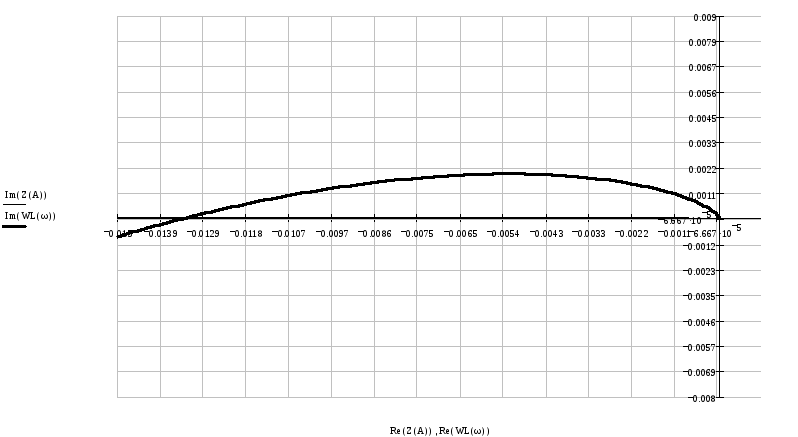
Получаем графикиW_лч(jω) и -1/Z _НЭ(A):

Рис.6 определение ПР

Рис. 6 определение ПР

рис. 5 определение ПР

Рис.5 определение ПР

Из графика видно (рис. 6), что кривые пересекаются, следовательно, в данном случае периодический режим существует.

Построим кривую , пренебрегая произведением.

рис.7 определение ПР без

Рис. 7 определение ПР без

Из графика видно (рис. 7), что кривые не пересекаются, следовательно, и в данном случае периодический режим не наблюдается. Значит чем больше значение , то тем круче будет проходить.

Влияние параметров лч и нэ на процессы в знсау. Рекомендации по стабилизации системы

Определим как влияет изменение параметров ЛЧ: k_лч , Т₁ ,Тм и НЭ: c на процессы в системе.

а) Оценка влияния параметров статической характеристики релейного усилителя

Значение c

При уменьшении c например при c<5.9 в системе периодический режим не происходит, что мы наблюдаем на графике (рис. 8) W_лч(jω) и -1/Z _НЭ(A), например, с=5:

Рис. 8 при с=5

При с>17800не будет пересеченияW_лч(jω) и -1/Z _НЭ(A), а следовательно в этом случае периодического режима возникать не будет (рис. 9). Например, при с=20000.

Рис. 9 при с=20000

При5.9<с<17800будет возникать периодический режим (рис. 10), например, при с=16000:

Рис. 10при с=16000

б) Оценка влияния параметров линейной части.

1) Общий коэффициент усиления линейной части k_лч.

При уменьшении k_лч в системе периодического режима не будет возникать, так как W_лч будет проходить более круче, например, при k_лч=0.0047 (рис. 11):

Рис.11 при k_лч=0.0047

При увеличенииk_лч процесс в системе затухает с медленней скоростью. Например при k_лч=2 (рис.12 ), где частота и амплитуда системы резко возрастает:

Рис. 12 при k_лч=2

Как видно из рисунка (рис. 12) мы наблюдаем пересечение двух кривых, то в этом случае возникает периодический режим.

2) Значения электромеханической постоянной времени двигателя Т_м и постоянной времени линейного усилителя Т₁.

При увеличении суммы T₁+T_м≥0.03926 система будет затухать с большей скоростью, а также при этом возникает периодический режим, например при T₁+T_м=2.03925 (рис.13):

При уменьшении суммы (T₁+T_м) процесс в системе затухает с большей скоростью, например при значении T₁+T_м=0.03926 (рис. 14), где частота и амплитуда резко уменьшается:

Рис.14 при T₁+T_м=0.03926

ВЫВОД:

Таким образом, система изначально находится в стабильном режиме, так как нет периодического режима. Можно использовать следующие методы для стабилизации системы, т.е. для того, чтобы в системе был затухающий процесс:

1. Изменение параметров НЭ:

– уменьшить значение с≤5.9и увеличить с>17800 нелинейного элемента.

2. Изменение параметров ЛЧ:

– уменьшить значение коэффициента усиления приk_лч;

– уменьшить значение суммы постоянных времени при T₁+T_м.

Итак, 2-мя методами (методом построения фазового портрета и частотно-амплитудным методом) система была исследована на существование периодического режима. При построении фазового портрета мы пренебрегли произведением Т₁*Т_ми нарисовали фазовый портрет с помощью уравнения 2-ого порядка, где наглядно видно, что периодического режима нет. С помощью частотно-амплитудным методом мы учитывали Т₁*Т_ми на графике наглядно видно, что есть периодический режим, т. е. в этом методе строили графики с помощью уравнения 3-его порядка.