5. Построение лачх и лфчх.

1. Запишем передаточную функцию разомкнутой системы.

2. Заменим в передаточной функции p на jω. После подстановки передаточная

функция примет следующий вид:

3. Разобьем передаточную функцию на:

– вещественную часть

– мнимую часть

4. Строим ЛАЧХ и ЛФЧХ:

т.М1 ( 0,25; 0 )

Рис. 6 Логарифмическая амплитудно–частотная характеристика

Рис. 7 Логарифмическая фазо–частотная характеристика.

–запас устойчивости по фазе γ = 108°.

–запаса устойчивости по амплитуде  = 11⁰ .

т. Р1 ( 1,55; -180 )

2. Нелинейная часть.

Структурная схема с нелинейным элементом имеет вид:

W1

W2

Н.Э.

W3

W4

W5

Рис.8 Структурная схема нелинейной системы

W1(p)=2.18 W2(p)=W3(p)=W4(p)=

W5(p)=

Нелинейный элемент имеет статическую характеристику вида:

Y

2

-0.5X

0.5

-2

Рис.9 Статическая характеристика нелинейного элемента

С точки зрения энергетических затрат, использование нелинейных элементов нецелесообразно. Проанализируем статическую характеристику данного нелинейного элемента на трех ее участках.

- передаточная функция звена.

Тогда на первом и третьем участках , то есть на этих участках система не работоспособна.

Работает система только на втором участке, где K==4 (равен тангенсу угла наклона прямой проходящей через начало координат).

Таким образом, нелинейный элемент в данной схеме целесообразней заменить линейным элементом с передаточной функцией Wne=K, где К=4 – коэффициент усиления.

Эквивалентная линеаризованная структурная схема примет вид:

W1

W2

Wne

W3

W4

W5

Рис. 10 Эквивалентная линеаризованная структурная схема

Определим передаточную функцию системы.

W6(p)=

2.1. Устойчивость линеаризованной системы

Проверим устойчивость системы по критерию Ляпунова. Для этого найдем корни характеристического полинома полученной передаточной функции.

-2.78

-33.3

solve, p -23.3

(0.36p+1)(0.03p+1)(0.043p+1)(0.072p+1)(0.93p+1)(15.02p+1) float, 3 -13.8

-1.08

-0.0666

Так как в результате получили шесть отрицательных корней, то, согласно критерию Ляпунова, можно сделать вывод, что система устойчива.

Если сравнить передаточную функцию, полученную в линейной части курсовой работы с передаточной функцией линеаризованной системы

, то можно сделать вывод, что их отличие мало. Следовательно, все характеристики также должны совпадать.

Для исследования данной системы ее структурную схему преобразовывают так, чтобы получить простую одноконтурную схему, в которой нелинейный элемент и линейная часть будут соединены последовательно.

2.2. Переходный процесс

Построим переходный процесс линеаризованной системы.

-передаточная функция замкнутой системы.

h(t)= …

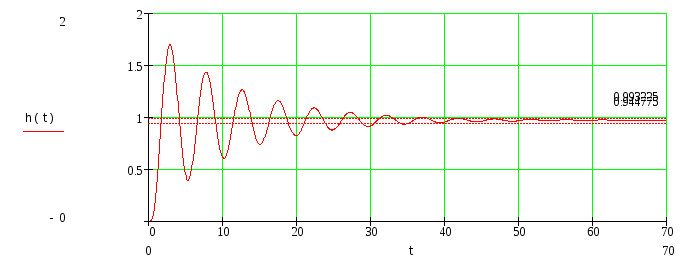
Рис. 11 График переходного процесса замкнутой системы

График переходного процесса аналогичен переходному процессу линейной части.

По графику переходного процесса определим прямые оценки качества системы:

1. время переходного процесса t_п =35 c

2. время первого согласования t₁=2 c

3. установившееся значение h_уст =0.969

4. максимальное значение h_мах =1.71

5. перерегулирование 76%

6. период колебаний Т=5с

7. время нарастания рег. Величены t_н=3с

8. колебательность n=7