
- •Кафедра управления и информатики в технических системах курсовая работа по дисциплине тау
- •1 Анализ линейной сау
- •1.1 Преобразование структурной схемы сау
- •1.2 Анализ устойчивости сау
- •2.4 Построение афчх системы
- •1.4 Построение ачх системы
- •1.5 Построение фчх и лачх системы
- •1.6 Построение переходного процесса
- •1.7 Анализ качества управления
- •2 Анализ нелинейной сау
- •2.1 Преобразование структурной схемы сау
- •2.2 Построение фазового портрета
Б АЛАКОВСКИЙ
ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
АЛАКОВСКИЙ
ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖИНЕРО – СТРОИТЕЛЬНЫЙ
Кафедра управления и информатики в технических системах курсовая работа по дисциплине тау
Исследование устойчивости линейных и нелинейных систем
автоматического управления
Выполнили ст. гр. УИТ-41
Данилова В.А.
Принял доцент каф. УИТ
Скоробогатова Т.Н._______
«___»_______________2003
2003
СОДЕРЖАНИЕ
1 Анализ линейной САУ 3
Задание 3
1.1 Преобразование структурной схемы САУ 4
1.2 Анализ устойчивости 6 1.3 Построение АФЧХ системы 7
1.4 Построение АЧХ системы 11
1.5 Построение ФЧХ 13
1.6 Построение переходного процесса 15
1.7 Анализ качества управления 17
2 Анализ нелинейной САУ 19
Задание 19
2.1 Преобразование структурной схемы САУ 20
2.2 Построение фазового портрета 22
Список использованной литературы 26
1 Анализ линейной сау
Вариант №55
ЗАДАНИЕ
Дана структурная схема САУ вида рисунка
1, с передаточными функциями звеньев:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Требуется проверить данную систему на
устойчивость, построить её частотные
характеристики и переходный процесс.
.
Требуется проверить данную систему на
устойчивость, построить её частотные
характеристики и переходный процесс.
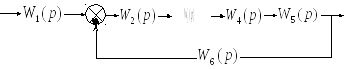 Рисунок 1
Рисунок 1
1.1 Преобразование структурной схемы сау
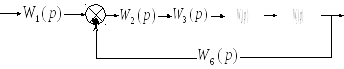
Рисунок 2
Звенья W2(p),W3(p),W4(p),W5(p) соединены последовательно, следовательно, имеем:
![]()
![]() ,
,
![]() .
.
В соответствии с данным преобразованием, структурная схема САУ примет вид:
![]()
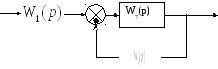
Рисунок 3
Звенья W6(p),W7(p) включены встречно – параллельно, следовательно:
![]() ,
,
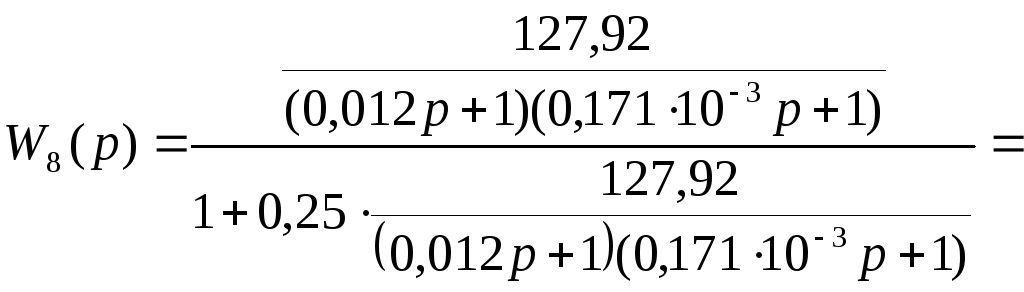
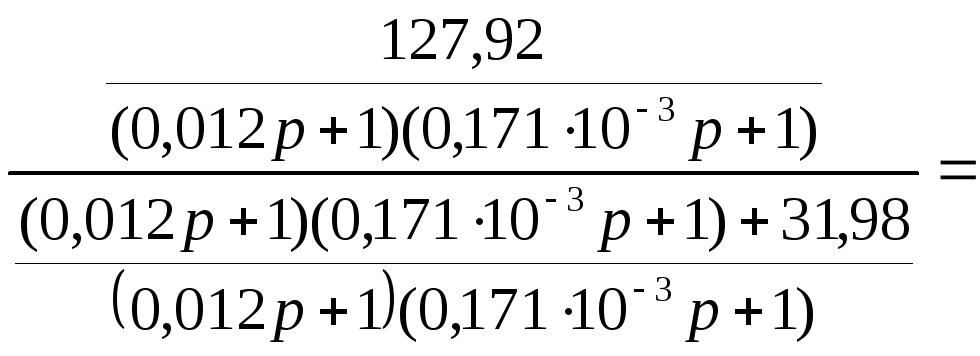
![]() .
.
Т огда:
огда:
Рисунок 4
Исходя из схемы рисунка 4, по правилу преобразования структурных схем, получим передаточную функцию системы:
![]() ,
,
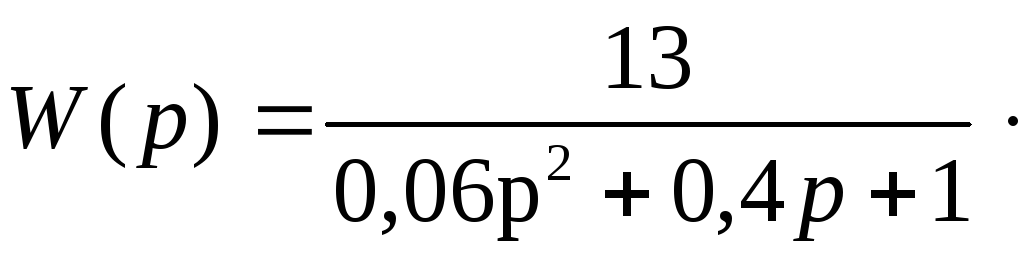
![]()
![]()
![]()
![]()
![]() .
.
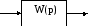 Получим:
Получим:
Рисунок 5
Т.е. передаточная функция системы имеет вид:
![]()
![]() .
.
1.2 Анализ устойчивости сау
Запишем характеристическое уравнение для рассматриваемой системы, получим:
![]() .
.
Характеристическое уравнение является уравнением 4-го порядка, коэффициенты которого положительны, а значит и корни все левые, из чего можно сделать вывод, что необходимое условие устойчивости выполняется.
Для определения устойчивости системы
воспользуемся критерием Гурвица, для
этого составим определители Гурвица
из коэффициентов характеристического
уравнения:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
=0,63;
=0,019;

![]() ;
;
![]() .
.
![]()
Согласно критерию Гурвица, система
устойчива, т.к. определители имеют
одинаковые знаки с коэффициентом
![]() .
.
2.4 Построение афчх системы
Для того чтобы построить АФЧХ, охватим всю систему обратной отрицательной связью, т.е.:

Рисунок 6
Следовательно, общая передаточная функция вычисляется по формуле:
![]() ;
;

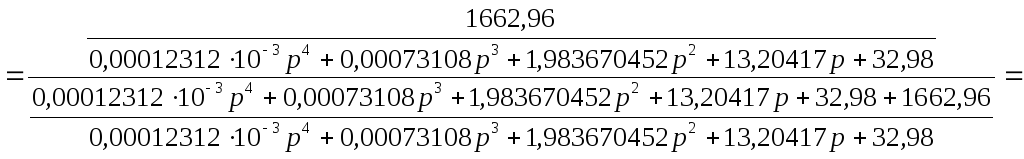
![]()
Т.е.:
![]() .
.
Перейдем от операторной формы записи передаточной функции к передаточной функции, записанной в изображениях по Лапласу.
![]() .
.
Получим частотную форму записи передаточной функции, для этого произведем замену S=j.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Получим действительную и мнимую части:
![]()
![]()
![]()
![]() .
.
Построим АФЧХ системы:
![]()
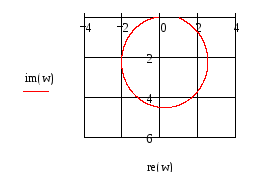
Рисунок 6
Построение ведем по дискретным значениям частоты ω. Таблица значений приведена ниже.
Таблица 1
|
|
|
|
|
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 125 130 |
0.98052997157918322582 1.0084485009018784885 1.1019372159571485472 1.2989171166204859743 1.7031455359304846680 2.4497450832331243372 -0.99200703940622451579 -1.6852283584907447707 -1.0174245719148391201 -0.68140407884800887984 -0.49467475098085696182 -0.37892889424957109749 -0.30138490392702830738 -0.24644766895131822463 -0.20586691793997478742 -0.17490666369799117423 -0.15067027173732774446 -0.13129468170258978653 -0.11553174628309174711 -0.10251664739608098455 -9.1632996824093312133∙10-2 -8.2430777691210490411∙10-2 -7.4574559037687050079∙10-2 -6.7809766324934812594∙10-2 -6.1940101632000652401∙10-2 -5.6812060374720179205∙10-2 -5.2304086520400463154∙10-2 |
0 -4.0384206375094887931∙10-2 -9.6620294594600036642∙10-2 -0.20331126042190430504 -0.48733020729596249604 -1.7113057482790731256 -4.1828602890835266876 -0.98927106211866177453 -0.33145619060490940927 -0.15491871026006233880 -8.6248429455795480600∙10-2 -5.3235022345403594575∙10-2 -3.5119559198966672541∙10-2 -2.4246903265880167652∙10-2 -1.7286660681564814817∙10-2 -1.2609738072223806215∙10-2 -9.3465060877881177653∙10-3 -7.0002882791636129204∙10-3 -5.2717277840178526351∙10-3 -3.9723045708815438440∙10-3 -2.9788927247484640115∙10-3 -2.2085663177524794806∙10-3 -1.6039874643708245434∙10-3 -1.1246000099971785280∙10-3 -7.4114346359862597615∙10-4 -4.3213530784615182597∙10-4 -1.8155750699651811638∙10-4 |
Найдем запасы устойчивости по фазе и амплитуде. Для этого будем рассматривать график АФЧХ в окрестности точки (-1, 0·j) и фрагмент окружности единичного радиуса (рис.7).
h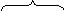
ψ
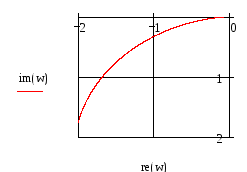

Рисунок 7
Получим:
-запас устойчивости по фазе ψ = 16,699 deg;
-запас устойчивости по амплитуде h=1.
