2 Разработка устройства управления

1. Синтез управления

Устройство управления (УУ) ищется та­ким, чтобы замкнутая система обладала астатизмом порядка =1 к задающему воздействию g. При этом время регулирования по задающему воздействию должно быть не более , а перерегулирование не более . Предполагается, что на вход УУ поступают два сигнала: задающее воздейст­вие g и управляемая переменная у. Относительная степень УУ равна .

Рассмотрим методику синтеза УУ по заданным показа­ниям качества, при =1, а заданная часть описывается уравнением [3]

_(2.1)

где у - управляемая переменная системы;

- возмущение (для рассматриваемой следящей системы ,а ),

причем ,

Будем предполагать также, что полином В(р) в (9) является числом или полиномом, удовлетворяющим условиям Гурвица, т.е. В(р) =

Так как заданный объест управления является минимально-фазовым, поэтому можно синтезировать систему, полагая характеристический полином замкнутой системы равным

_(2.2)

где ,

- ко­эффициент полинома В(р) при p в старшей степени т;

- гурвицевый полином, выбираемый по условиям качества синтезируемой системы.

- полином, имеющий нули, равные тем нулям полинома А(р), модуль реальной части которых является достаточно боль­шим, т.е. эти нули располагаются в области , комплексной плоскости, допустимой для дайной системы. Выражения для высокочастотной и низкочастотной составляющей запишутся в виде [1]

_(2.3)

_(2.4)

В соответствии с рассматриваемым методом синтеза сначала ищется уравнение «вход-выход» искомого УУ в виде [1]

R(p)u = Q(p)g-L(p)y, (2.5)

где R(p), Q(p), L(p) -полиномы, подлежащие определению в процессе синтеза. При этом по условиям физической реализуемости должны выполняться неравенства

(2.6)

или

где - заданная относительная степень УУ. Относительная степень УУ зависит от свойств элементов, из которых строится синтезируемое УУ.

Как видно, УУ (2.1) имеет, в общем случае, не менее двух входов по задающему воздействию g и по управляемой переменной - у (выходу системы), поэтому оно и называется двумерным устройством управления (ДУУ).

Относительной степенью управляемой ди­намической системы называется минимальный порядок производ­ной по времени от выхода системы, которая явно зависит от управ­ления. В случае линейного ДУУ его относительная степень

(2.7)

Для обеспечения астатизма порядка v_g по задающему воздействию необходимо, чтобы в разомкнутой цепи системы управления было v_g интеграторов. Если

(2.8)

причем v₀ < v_g , то в ДУУ необходимо ввести

(2.9)

интеграторов. Подставляя заданные значения в (2.9) получим

Таким образом очевидно что вводить в ДУУ дополнительные интеграторы не нужно.

Для определения уравнения «вход-выход» искомого УУ (2.5) применяют следующие формулы

(2.10)

(2.11)

где , - неизвестные пока полиномы. При этом характеристический полином D(p) замкнутой системы имеет вид

(2.12)

Так как в этом равенстве

, (2. 13)

то сокращая общие множители и ,подставляя получим

(2. 14)

или подставляя , =1,95 и выражение (2.4), получим

. (2. 15)

Степень полинома в (2.15), равна степе­ни произведения . Следовательно, в системе уравнений, которой эквивалентно полиномиальное уравнение (6.15), содержится

N_y =+ 1

уравнений и

N_k=+ 1 + +1=+ +2

неизвестных коэффициентов, т.е.

N_y N_y =+ 1=+ ,

N_k=

Для разрешимости указанной системы необходимо, чтобы выполнялось следующее условие

N_k =N_у.

Отсюда, используя приведённые выражения, найдём неизвестные величины( при )

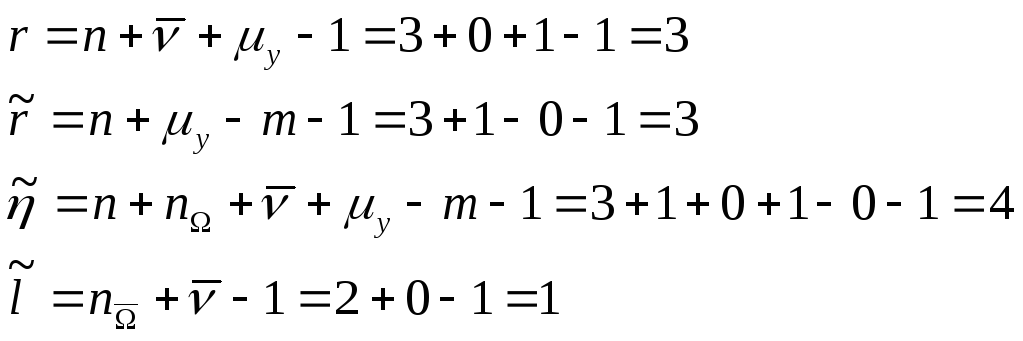
Для выбора коэффициентов полинома степени пользуются стандартные передаточные функции [1]. По заданному порядку астатизма =1 , степени =5 и перерегулированию выбираются коэффициенты и величина .

Таблица 6.1

Порядок астатизма	Степень знаменателя	Коэффициенты						Перерегулирование	Время регулирования ,с	Примечание
1	5	1	3,64	5,46	5,3	2,6	1	нет	5,7	Минимальное время регулирования

Далее вычисляются временной масштабный коэффициент

а затем желаемые коэффициенты полинома по формуле

(2. 16)

Подставляя выбранные коэффициенты, получим

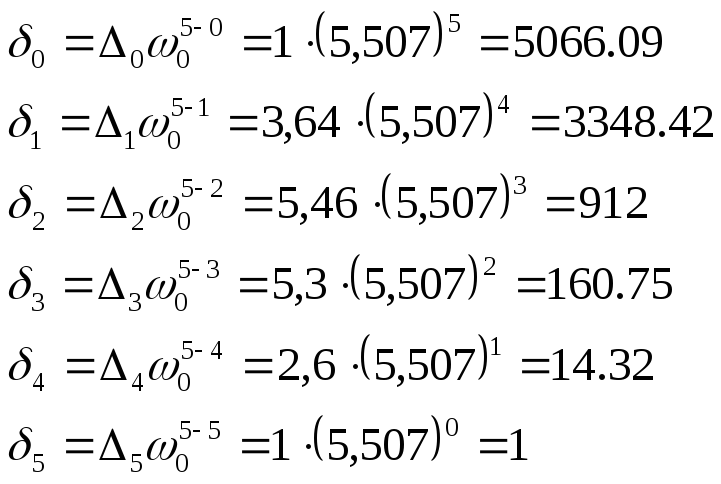
После этого записывается соответствующая система уравнению (2.15) система следующего вида:

(2.17)

Матрица этой системы имеет +1=2 столбцов, составленных из коэффициента , и +1 =4 столбцов, составленных из коэффициентов полинома

_{Получим систему}

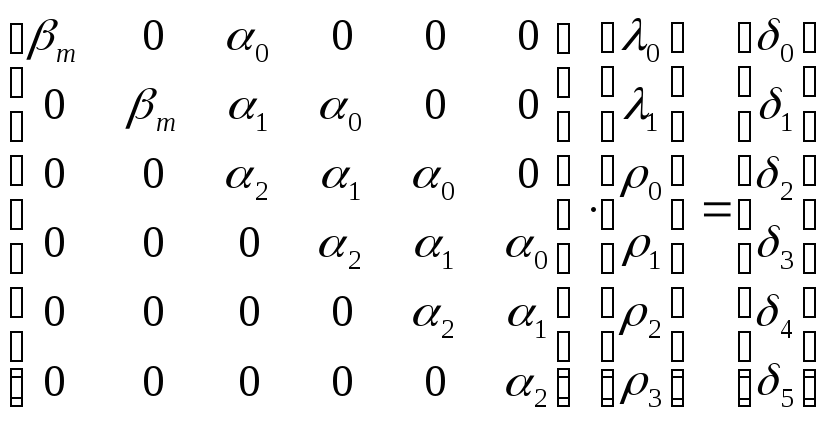
_{Подставив численные значения, получим}

_{Перемножив матрицу на столбец получим систему уравнений}

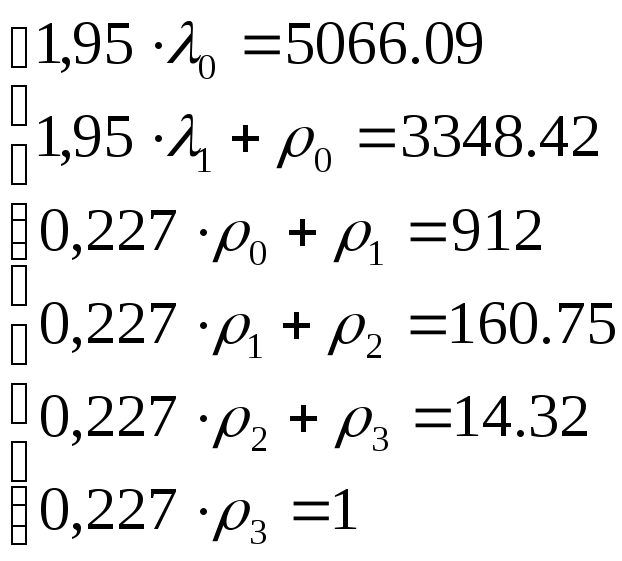(2.18)

Решая систему уравнений (2.18) относительно и , получим численные значения коэффициентов полиномов и

Решение системы (2.18) позволяет записать полиномы:

(2.19)

(2.20)

а затем полиномы R(p), L(p) по приведённым выше выражениям (2.10),(2.11).

Полином Q(p) определяется по формуле

(2.21)

Подставив известные значения и выражение (2.4) получим

Проверим условие физической реализуемости по (2.6)

Условие выполняется.

Таким образом, найдены все полиномы ДУУ, и можно записать его уравнение по формуле (2.5). В синтезируемой следящей системе измеряемыми являются отклонение

(2.22)

и управляемая переменная , а управлением – напряжение на входе усилителя мощности Поэтому заменяя в формуле (2.5) g по формуле (2.22) и приводя подобные, получим следующее уравнение

R(p)U_y = Q(p) – (L(p) - Q(p) ), (2.23)

Подставим раннее найденные полиномы R(p), Q(p) и L(p) в (2.23)

()U_y = () –

-((5)-()),

Приведем подобные и в результате получим уравнение

()U_y = () -

-()) (2.24)

Наконец, заменяя в уравнении (2.23) и из выражений (1.2), (1.4), получим уравнение физически реализуемого ДУУ

(2.25)

Подставив найденные полиномы, получим

_{Упростив выражение, получим:}

(2.26)

Уравнение (2.26) позволяет представить схему синтезированной следящей системы в виде, показанном на рисунке 2.1

Рисунок 2.1 – Структурная схема следящей системы

На рисунке 2.1 символом ИУ обозначены исполнительные элементы следящей системы: усилитель, двигатель и редуктор, а символом РДДУ – реализуемое двумерное устройство управления.

2. Описание схемы модели и результатов моделирования разработанной следящей системы.

Структурная схема следящей системы, выполненная с учетом выражения (6.26) и схемы 2.1 выполненная в MatLab показана на рисунке 2.2.

Рисунок 2.2 – Структурная схема следящей системы, выполненная в MatLab

Произведем моделирование переходных процессов в системе, подавая на ее вход сначала единичную ступенчатую функцию, затем линейно – нарастающее воздействие, при отсутствии и наличии момента сопротивления нагрузки

.

В результате моделирования получим следующие графики, показанные на рисунках 2.3 – 2.6.

Рисунок 2.3 – Переходная функция системы без момента сопротивления нагрузки

Время регулирования на основе переходной характеристики 1,4 с.

Рисунок 2.5 – Реакция системы на линейно – нарастающую функцию без момента сопротивления нагрузки

Скоростная онибка равна 0,7 радиан. На основе анализа графиков можно заключить, что система обладает астатизмом первого порядка.

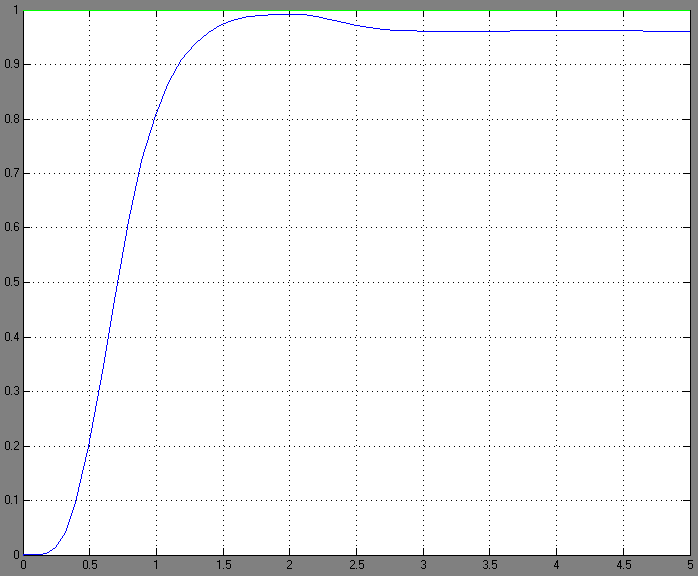
Рисунок 2.4 – Переходная функция системы с моментом сопротивления нагрузки

Время регулирования 1.45с.

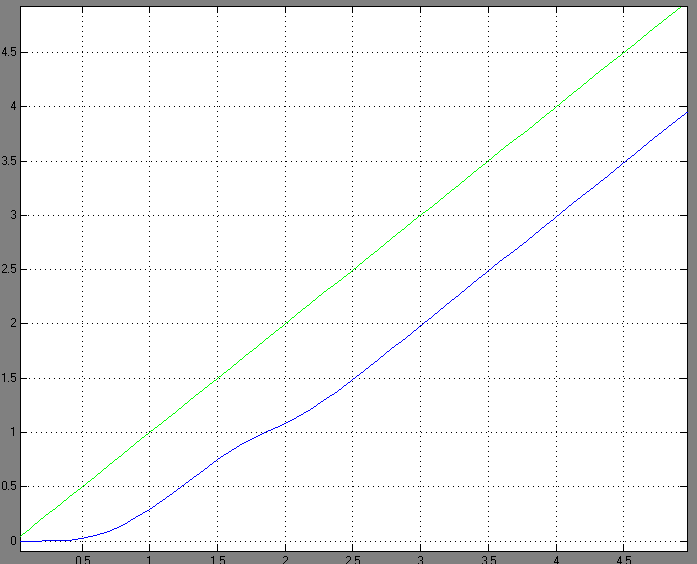
Рисунок 2.5 – Реакция системы на линейно – нарастающую функцию с моментом сопротивления нагрузки