
- •Введение
- •Оу (бункер и питатель)
- •Построение ачх линейной части системы
- •Определение устойчивости линейной части системы по критерию Гурвица
- •Определение устойчивости линейной части системы по критерию Найквиста
- •3.5 Построение переходного процесса импульсной системы
- •Заключение
- •Список использованной литературы
-
Построение ачх линейной части системы
АЧХ строиться для того, чтобы определить косвенные оценки качества системы.
Для
того, чтобы определить АЧХ системы,
необходимо в передаточной функции
![]() р заменить на jw,
знаменатель уравнения помножить на
сопряженное выражение, выделить мнимую
и вещественную части по формулам
определить АЧХ:
р заменить на jw,
знаменатель уравнения помножить на
сопряженное выражение, выделить мнимую
и вещественную части по формулам
определить АЧХ:
АЧХ:
![]() ,
(16)
,
(16)
где
![]() - действительная часть передаточной
функции;
- действительная часть передаточной
функции;
![]() -
мнимая часть передаточной функции.
-
мнимая часть передаточной функции.
Используя прикладную программу MathCAD вычислим АЧХ по формуле (13). График АЧХ изображен на рисунке 7.
Определим по графику косвенные оценки качества системы:
- амплитуда при нулевой частоте A(0)=1;
- максимальная амплитуда Аmax=5.2;
- резонансная частота wp=180 Гц;
- частота среза, при которой амплитуда, равна 0.1 wcp=475 Гц;
-
полоса пропускания (промежуток частот,
при котором значения амплитуды больше
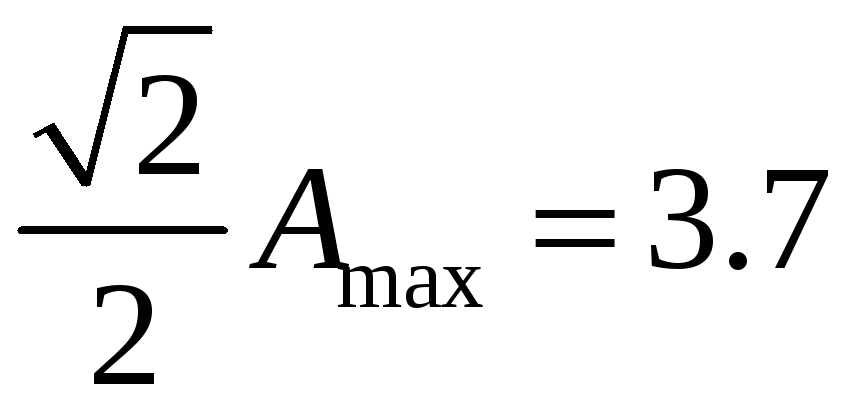 ):
175 Гц<
):
175 Гц<![]() <200
Гц.
<200
Гц.
, Гц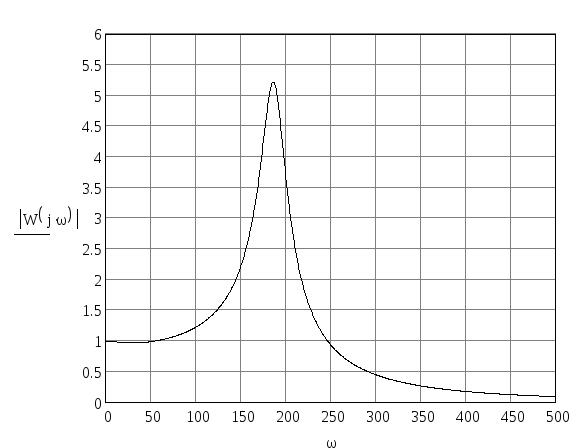








Рисунок 7 – Амплитудо – частотная характеристика линейной части системы
-
Определение устойчивости линейной части системы по критерию Гурвица
Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительными.
По коэффициентам характеристического уравнения составляется определитель Гурвица. Характеристическое уравнение – это знаменатель передаточной функции:
![]() (17)
(17)
Выпишем коэффициенты характеристического уравнения:
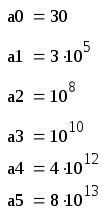
Для нахождения определителя по главной диагонали выписываются все коэффициенты характеристического уравнения, начиная со второго, затем вверх записываются коэффициенты с возрастающим индексом, а вниз с убывающим индексом.
Составленный определитель называется главным определителем Гурвица, он имеет порядок совпадающий с порядком характеристического уравнения. Из главного определителя составляются частные определители первого, второго, третьего и так далее порядков их образования из главного определителя.
Вычисляя главный определитель и частные определители, Гурвиц установил, для того, чтобы система была устойчива необходимо и достаточно, чтобы все определители были положительны. Если хотя бы один определитель отрицательный, то система неустойчива.
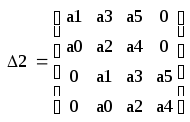
Определитель Гурвица и миноры для данного характеристического уравнения:
 (18)
(18)
![]() >0
>0
 (19)
(19)
![]() >0
>0
 (20)
(20)
![]() >0
>0
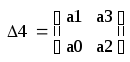 (21)
(21)
![]() >0
>0
![]() a1=3*105
>0 (22)
a1=3*105
>0 (22)
Все миноры определителя Гурвица больше ноля, следовательно система устойчива.
-
Определение устойчивости линейной части системы по критерию Найквиста
Критерий
Найквиста позволяет по годографу
амплитудной фазовой характеристики
системы судить об устойчивости замкнутой
системы. Годограф имеет действительную
![]() и мнимую
и мнимую
![]() оси,
на которых откладываются соответственно
действительные и мнимые значения
передаточной функции
оси,
на которых откладываются соответственно
действительные и мнимые значения
передаточной функции
![]() в зависимости от частоты. Критерий
Найквиста можно сформулировать следующим
образом: САР, устойчивая в разомкнутом
состоянии, будет устойчива в замкнутом
состоянии, если годограф не охватывает
точку (-1, j0).
В противном случае, при неустойчивости
системы, годограф охватывает эту точку
в положительном направлении
в зависимости от частоты. Критерий
Найквиста можно сформулировать следующим
образом: САР, устойчивая в разомкнутом
состоянии, будет устойчива в замкнутом
состоянии, если годограф не охватывает
точку (-1, j0).
В противном случае, при неустойчивости
системы, годограф охватывает эту точку
в положительном направлении
![]() раз, где p
– количество корней.
раз, где p
– количество корней.
Построим годограф, используя MathCad. На графике присутствуют обозначения:
![]()
![]() -
мнимая часть передаточной функции
W(jω).
-
мнимая часть передаточной функции
W(jω).
![]()
 -
действительная часть передаточной
функции W(jω).
-
действительная часть передаточной
функции W(jω).



Рисунок 8 – Годограф Найквиста
Система является устойчивой, поскольку годограф Найквиста не охватывает точку с координатами (-1;0).
Вывод.
Проведя ряд упрощений предложенной исходной схемы, была получена передаточная функция, преобразовав которую, был получен ряд значений характеризующих систему.
Анализ этих значений и характеристик показывает, что система устойчива и точна в регулировании. Система имеет затухающий периодический переходный процесс.
Для
системы массобмена аппарат работает
весьма быстро, так как время регулирования
системы tр=1.9c.
Полоса пропускания частот системы
175Гц<![]() <200Гц.
<200Гц.
2 ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ ЧАСТИ СИСТЕМЫ
2.1 Структурная схема с нелинейным элементом
Добавим в схему нелинейный элемент NLE с нелинейной характеристикой реле с гистерезисом. Полученная схема приведена на рисунке 9, статическая характеристика элемента – на рисунке 10.
WОУ WРег.
1 WРег.
2 WИМ1 WИМ2
WДm WДрасх NLE



















u
Рисунок 9 – Структурная схема нелинейной системы
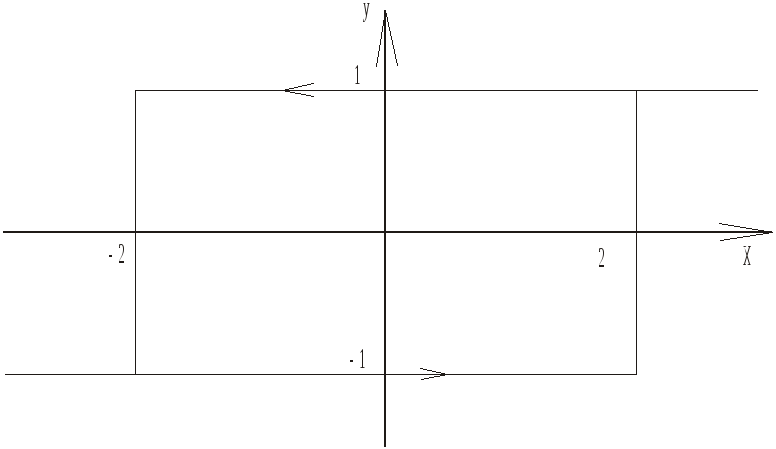
Рисунок 10 - Статическая характеристика нелинейного элемента
Численные значения передаточных функций описываются выражениями (1) – (8).
Отрезок (-2, 2) называется шириной петли гистерезиса, в ряде случаев ширина петли должна быть большой и это является полезным для системы, а в ряде случаев петля гистерезиса приводит к нежелательным последствиям, поэтому ее стремятся уменьшить. Приведенной характеристикой обладают электромагнитные реле и электромагниты. Обычно для электромагнитный реле величина «2» называется порогом срабатывания, а величина «-2» - порогом отпускания.
2.2 Упрощение структурной схемы нелинейной системы
По правилам преобразования структурных схем преобразуем нелинейную систему (рисунок 11):
![]() (23)
(23)
![]() (24)
(24)
 (25)
(25)
![]() (26)
(26)
W4 A


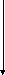
W3 W1 u NLE









W2


Рисунок 11 – Вид 1 структурной схемы нелинейной системы
Перенесем узел А через звено W3, получаем схему, изображенную на рисунке 12. В итоге получаем схему, изображенную на рисунке 13. Полученные промежуточные передаточные функции:
![]() (27)
(27)
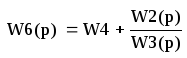 (28)
(28)
W3 W1 W4 W2 u NLE 1/W3 A















Р исунок
12 - Вид 2 структурной схемы нелинейной
системы
исунок
12 - Вид 2 структурной схемы нелинейной
системы
Рисунок 14 - Вид 3 структурной схемы нелинейной системы
Полученную схему разрываем в месте обратной связи и насильственно замыкаем данную цепь единичной ООС (рисунок 15) и запишем уравнение линейной части:
![]() (29)
(29)
Используя программу MathCad для преобразования функций, получим выражение вида:
 (30)
(30)
Wл NLE








u
Рисунок 15 - Вид 4 структурной схемы нелинейной системы
2.3 Построение фазового портрета
Передаточная
функция линейной системы есть
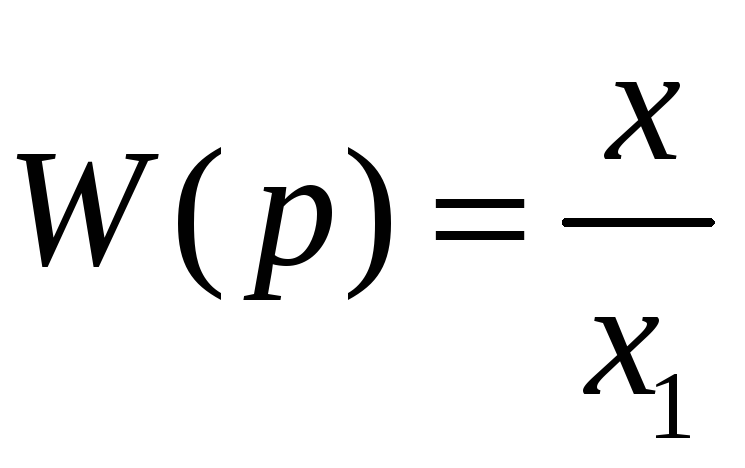 или
или
![]() (31)
(31)
Подставляя в формулу (31) значение передаточной функции получим:
 (32)
(32)
Приведенную формулу можно записать в виде:
![]() (33)
(33)
Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.
Введем
замену
![]() и исключим из правой части уравнения
производную:
и исключим из правой части уравнения
производную:
![]() (34)
(34)
Для того чтобы построить фазовый портрет, необходимо, чтобы степень числителя и знаменателя не превышала вторую степень, поэтому элементы выше второй степени исключаем. Тогда получим:
![]() (35)
(35)
![]() (36)
(36)
![]()
Так
как в качестве нелинейного элемента
используется реле с гистерезисом со
статической характеристикой, представленной
на рисунке 10, то подставляя значение
![]() для четырех участков, получим систему:
для четырех участков, получим систему:
 (37)
(37)
Создадим матрицу для решения дифференциального уравнения в программе MathCad:
 (38)
(38)
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для двух начальных условий:
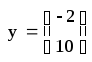 ,
,
 (39)
(39)
Возьмем количество точек равным 1000 и конечное время интегрирования 200, то матрица решений запишется как:
 (40)
(40)
Построим фазовый портрет


Рисунок 17 - Фазовый портрет нелинейной системы
Построим переходные процессы нелинейной системы.
t
, с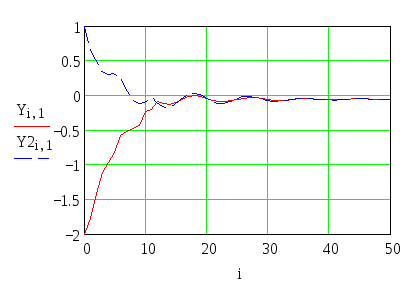

Рисунок 18 – Переходный процесс нелинейной системы
Вывод.
На рисунке 17 представлен фазовый портрет нелинейной системы. Из графика видно, что при различных начальных условиях система будет оставаться устойчивой. С течением времени процесса амплитуда колебаний будет уменьшаться, система придет к устойчивому равновесию – точке (-0,2;11) на рисунке 17, то есть произойдет процесс переключения. Устойчивость системы подтверждает график переходного процесса.
3 Исследование системы с импульсным элементом
3.1 Техническое задание
По заданию проведем z-преобразование данной системы. Для этого первый элемент системы (регулятор 2) на рисунке 2 и сумматор заменим на цифровой элемент.
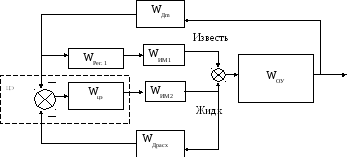
Рисунок 19 – Структурная схема импульсной системы
Передаточная функция цифрового элемента: Wцэ принимаем равным единице. Другие значения передаточных функций приведены в выражениях (1) – (8).
3.2 Нахождение передаточной функции замкнутой системы
Упростим структурную схему (показано на рисунке 20). Передаточные функции элементов:
![]() (41)
(41)
![]() (42)
(42)
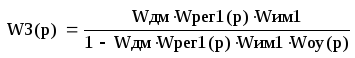 (43)
(43)
![]() (44)
(44)
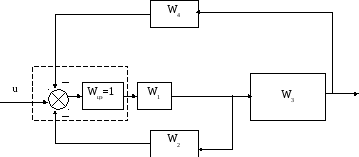
Рисунок 20 – Вид 1 структурной схемы цифровой системы
Найдем общую передаточную функцию замкнутой системы:
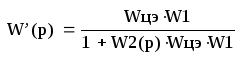 (45)
(45)
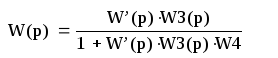 (46)
(46)
W(р)=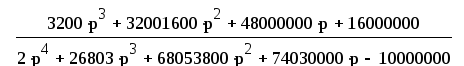 (47)
(47)
3.3 Проведение z-преобразования
Для импульсных систем характерно построение решетчатых функций.
Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа.
Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него.Z-преобразование проведем по формуле:
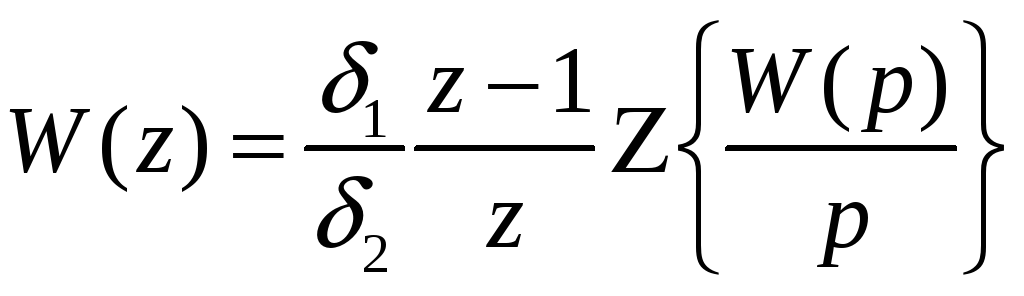 ,
(48)
,
(48)
где
![]() и
и
![]() - показатели цифрового преобразования.
В рамках курсовой работы принимает их
равными 1;
- показатели цифрового преобразования.
В рамках курсовой работы принимает их
равными 1;
![]() -
передаточная функция импульсной системы.
-
передаточная функция импульсной системы.
Воспользуемся программным продуктом MathLAB для получения искомой передаточной функции уже в форме z-преобразования. Создадим переменную передаточной функции:
>> W=tf([3200 32001600 48000000 16000000],[2 26803 68053800 74030000 10000000]);
Проведем z-преобразование с осуществлением выборки времени 0.6:
>> W=c2d(W,0.6)
Transfer function:
0.5792 z^3 - 0.7621 z^2 + 0.2448 z + 3.185e-018
-------------------------------------------------------
z^4 - 1.482 z^3 + 0.5205 z^2 + 2.649e-017 z + 9.01e-035
Получили передаточную функцию:
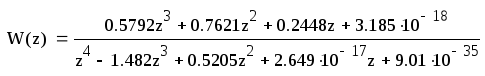 (49)
(49)
3.4 Определение устойчивости системы
Алгебраический критерий Шур-Кона по характеристическому уравнению замкнутой системы позволяет судить об устойчивости импульсной системы. В нашем случае получили характеристическое уравнение:
![]() (50)
(50)
Корни характеристического уравнения
![]() (51)
(51)
будут лежать внутри единичной окружности (что указывает на устойчивость системы), если его коэффициенты удовлетворяют следующим условиям:
![]() для
нечетных определителей,
для
нечетных определителей,
![]() для
четных определителей,
для
четных определителей,
где
![]() - определить Шур-Кона.
- определить Шур-Кона.
Коэффициенты характеристического уравнения для исходной передаточной функции импульсной системы:
![]()
![]()
![]()
![]()
Составим определители Шур-Кона:
 (52)
(52)
 (53)
(53)
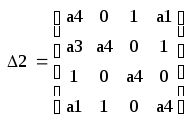 (54)
(54)
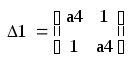 (55)
(55)
Подставив значения коэффициентов в выражения (52) – (55), получаем:

Таким образом, условия Шур-Кона выполняются, система является устойчивой.
