7. Построение графика переходной функции h(t) заданной нескорректированной системы в Matlab.
Переходная функцияh(t) звена – это реакция звена на единичное воз - действие1(t) при условии, что до момента приложения воздействия звено находилось в состоянии покоя, т.е. начальные условия были нулевыми.
Построим график переходной функции h(t) заданной нескорректированной системы в приложенииSimulinkпакетаMatlab.
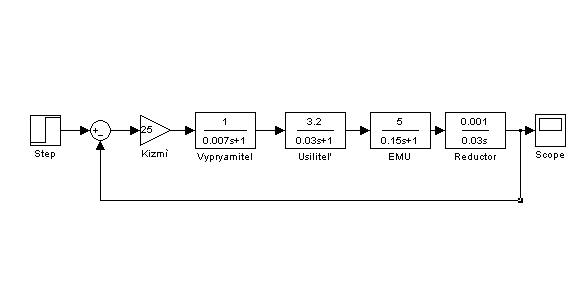
Рис. 7. Структурная схема замкнутой системы
Рис. 8. Переходный процесс нескорректированной системы (сходящийся)
Показатели качества нескорректированной системы:
Полученные значения показателей качества нескорректированной системы не удовлетворяют требуемым (tрег<=1.5;<=0%).
Оценка показателей качества нескорректированной системы
Перерегулирование нескорректированной системы не удовлетворяет требуемому (<=5%), а время регулирования лежит в пределах требуемых значений (tрег<=2.5).
8. Проведение синтеза последовательного корректирующего устройства методом Соколова
Передаточная функция замкнутой
нескорректированной системы: Фн/ск=
Исходя из технических
требований к системе, известно, что
перерегулирование системы должно быть
%,
а время регулирования
tр= 1.5 с, значит данная система в скорректированном состоянии должна удовлетворять второму условию закона распределения нолей и полюсов, когда достаточно медленное время регулирования, но перерегулирование системы мало. Для второго случая передаточная нормированная функция выглядит следующим образом:
Фн=
,
гдеn=np-mp+
зад-1=4-0+1-1=4
n=4, значит передаточная нормированная функция для данной системы будет иметь следующий вид:
Фн=
.
Зная нормированную передаточную
функцию Фн,
сформируем желаемую передаточную
функцию Фж(s)=Фн(
).Желаемая
передаточная функция выбирается с
использованием теоремы масштабов
преобразования Лапласа:
.
Тогда желаемая передаточная функция для данной системы будет иметь следующий вид:
Фж(s)=
Фн(
)=
=
=
=
=
p– аргумент нормированной передаточной функции,
s– комплексный аргумент Лапласа,
z– коэффициент масштаба времени,
tрег – заданное время регулирования,
–
время регулирования нормированной
передаточной функции.
Тогда передаточная функция корректирующего устройства имеет следующий вид:
Wку=
=
=
Найдем передаточную функцию скорректированной разомкнутой системы:
Wск=
=
9. Построение лах и лфх скорректированной разомкнутой системы в Matlab
Листинг программы:
w=tf([1],[ 0.007 0.076 0.367 0.882 0]);
margin(w);
Рис.9 Графики ЛАХ и ЛФХ скорректированной разомкнутой систем
Оценка запасов устойчивости скорректированной системы по модулю (амплитуде) и по фазе
Запас устойчивости по амплитуде
=10,4
дБ,m=1-L=0.7
Запас устойчивости по фазе
.
Значит, система обладает достаточными
запасами устойчивости, как по амплитуде,
так и по фазе.
Сравнение с запасами устойчивости нескорректированной системы
После введения корректирующего устройства система стала более устойчивей, что наглядно видно из ЛАХ и ЛФХ скорректированной разомкнутой системы по увеличению запасов устойчивости по модулю (m=0.7) и по фазе (=62,7).
Построение графика переходной функции h(t) скорректированной системы в приложении Octave
Передаточная функция скорректированной замкнутой системы имеет следующий вид:
Фск=
Листинг программы:
w=tf([1],[0.007 0.076 0.367 0.882 1])
step(w)
Рис.10 График переходной функции скорректированной систем
Оценка показателей качества скорректированной системы
Время регулирования по графику примерно равно tp=1,5c.
Перерегулирование системы:
Таким образом, с помощью метода Соколова Н.И. было синтезировано последовательное корректирующее устройство, которое было введено в систему для достижения требуемых показателей качества. В результате была получена скорректированная система, удовлетворяющая требуемым показателям качества, но с незначительным отклонением величины перерегулирования: время регулирования равно 1.5 секунды и величина перерегулирования равна 3%.