курсовая работа / курсач-tau / Kurs1_1
.docАнализ линейной САУ.
По заданной структурной схеме системы управления вычислить эквивалентную передаточную функцию разомкнутой и замкнутой системы. Построить АФЧХ разомкнутой и замкнутой системы. Исследовать устойчивость по одному из критериев. Определить запасы устойчивости системы по амплитуде и по фазе. Построить переходный процесс системы методом трапеций, по переходному процессу провести анализ качества управления и определить все его показатели. При необходимости дать рекомендации методов улучшения этих параметров.
x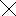
вх xвых
Kc
Рис. 1 – Структурная схема
Исходные данные:
|
Ke = 0.56; |
Td = 0.2; |
Ce = 0.036; |
|
KU = 198; |
Tm = 0.34; |
jp = 218. |
|
K0 = 0.43; |
T0 = 0.58; |
|
АФЧХ разомкнутой и замкнутой системы.
Вычислим эквивалентную передаточную функцию разомкнутой и замкнутой системы.
;
;
;
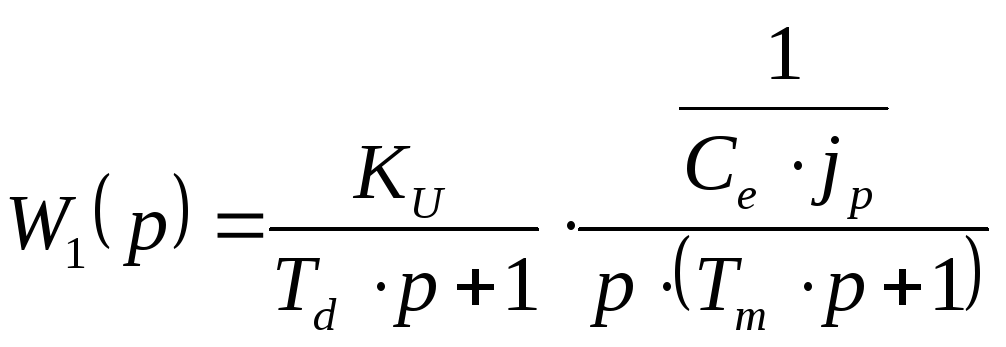Упростим данное выражение
;
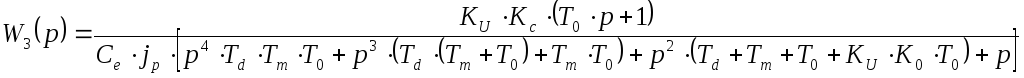Введем новые переменные
получим следующее выражение
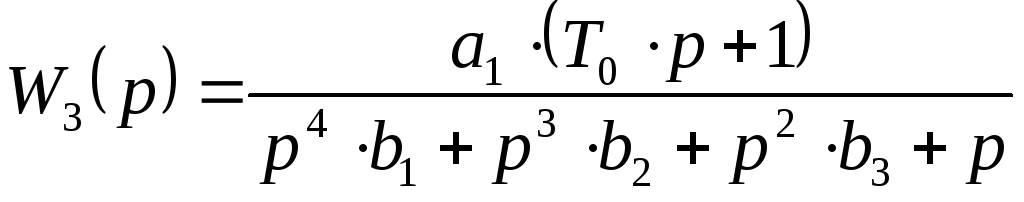
Построим АФЧХ, для этого заменим p = j
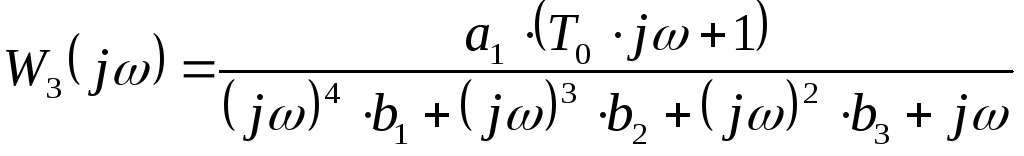
Преобразуем выражение и выделим вещественную и мнимую часть
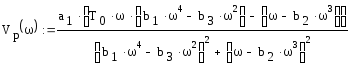
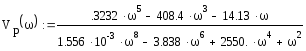
График АФЧХ разомкнутой системы представлен на рис.1, см. Приложение 1. На рис.2, Приложения 1, представлен график АФЧХ разомкнутой системы в вблизи точки (0;j0).
Передаточная функция замкнутой системы
Упростим выражение
;
Построим АФЧХ, для этого заменим p = j
;
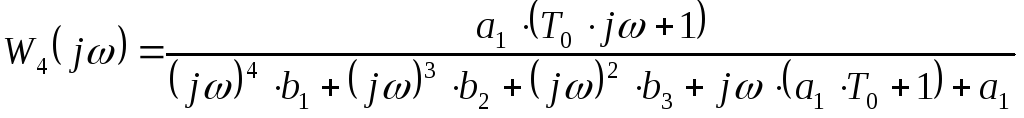Преобразуем выражение и выделим вещественную и мнимую часть
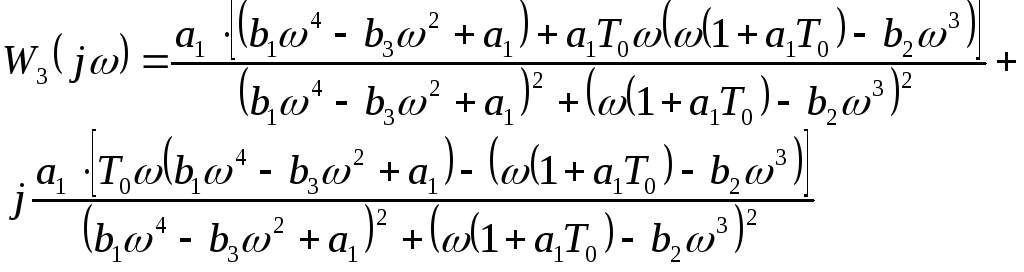
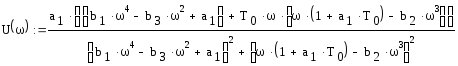
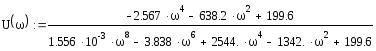
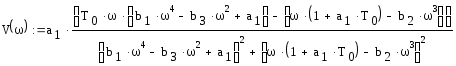
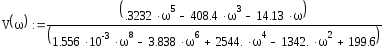
График АФЧХ замкнутой системы представлен на рис. 3, см. Приложение 1. На рис. 4, Приложения 1, представлен график АФЧХ в вблизи точки (0;j0).
Определение устойчивости системы.
Для определения устойчивости системы воспользуемся критерием Гурвица.
Критерий Гурвица: для того чтобы система управления была устойчива необходимо и достаточно, чтобы выполнялось неравенство а0 > 0, а все определители Гурвица были положительными.
Характеристическое уравнение имеет вид:
или
введем обозначение
с0 = b1;
c1 = b2;
c2 = b3;
c3 = a1T0+1;
c4 = a1.
Условие устойчивости с0 >0; с1 >0; с2 >0; с3 >0; с4 >0.
Определим определители Гурвица
c0 = 0.059 > 0;
c1 = 0.527> 0;
c2 = 27.294 > 0;
c3 = 7.841> 0;
c4 = 10.525> 0;
=
0.527
=
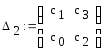
13.911
=
106.157
=
1.117E+3
Как видно из результатов, система по Гурвицу устойчива.
Используем графический метод Михайлова для определения устойчивости
Заменим p на j в выражении D(p)
выделим реальную и мнимую часть
Система будет устойчивой, если при
возрастании частоты
от 0 до вектор D(j)
повернется на угол
,
где n – степень
уравнения D(p)
= 0, или, что то же самое, если характеристическая
кривая при изменении частоты
от 0 до , начиная с
положительной действительной оси,
обходит последовательно в положительном
направлении, т.е. против часовой стрелки
n квадрантов.
На рис. 2 приведена характеристическая кривая. Степень уравнения D(p) = 0 равна n = 4, как видно из рисунка характеристическая кривая последовательно проходит 4 квадранта и в 4 квадранте уходит в бесконечность, что соответствует устойчивой системе.
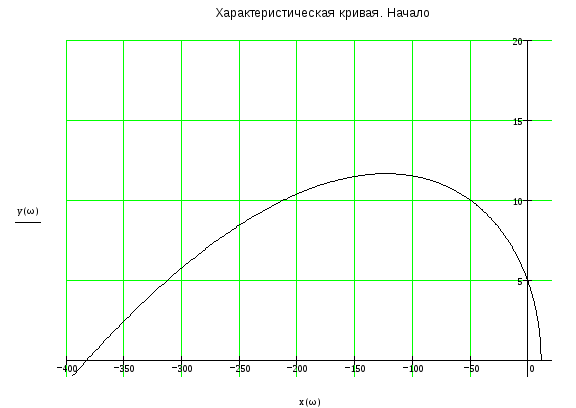
Рис. 2а – Характеристическая кривая. Область вблизи точки (0; j0)
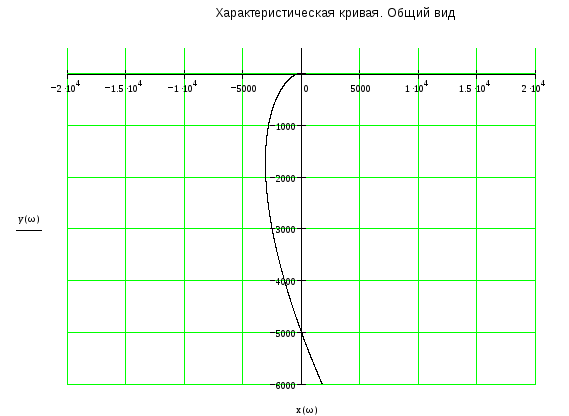
Рис. 2б.
Используя два критерия устойчивости, критерий Гурвица и критерий Михайлова, определили, что система является устойчивой.
Определение запаса устойчивости по амплитуде и по фазе.
Для этого построим ЛАХЧ и ФЧХ
;
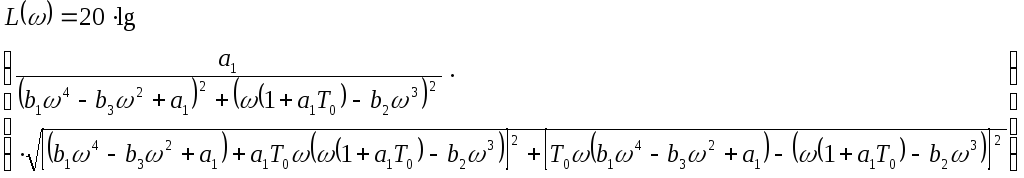
Подставим численные значения
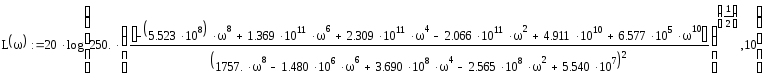
На рис. 5, Приложения 1, представлена ЛАЧХ характеристика.
ФЧХ определяется по следующей формуле
;
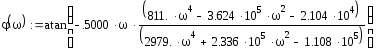
На рис. 6, Приложения 1, представлен график ФЧХ.
Из данного графика определим запасы устойчивости по амплитуде и по фазе
= 0.8719 при данной частоте L() = 0;
Запас по фазе равен = -61.722
= 21.141 при данной частоте = -180
Запас по амплитуде равен L() = 20 log (h) = -30.387 h = 0.03
Переходный процесс.
Построим переходный процесс методом трапеции.
Для этого построим график вещественной частотной характеристики
1 2 3 4
Рис. 3.
Разобьем вещественную частотную характеристику на трапециевидные частотные характеристики. Параметры трапеций занесем в таблицу.
Таблица №1
|
Трапеция |
Параметры трапеции |
|||
|
ro |
d |
n |
|
|
|
1 |
-1,2 |
0,25 |
0,45 |
0,56 |
|
2 |
3 |
0,45 |
0,6 |
0,75 |
|
3 |
-0,6 |
0,65 |
1,1 |
0,59 |
|
4 |
-0,2 |
1,1 |
5 |
0,22 |
На рисунке 3 представлены трапеции, сведенные большим основание к оси
1 2 3 4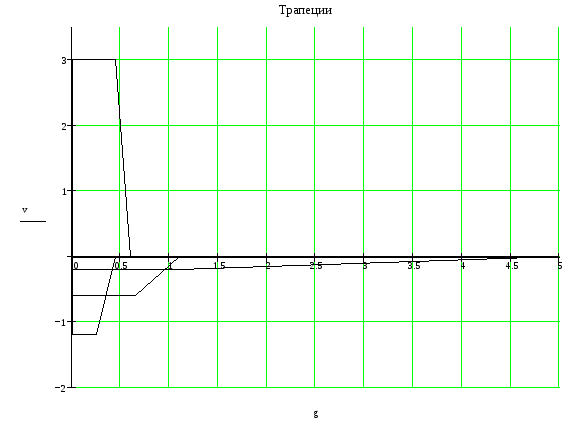
Рис. 4
Значения составляющих кривой переходного процесса. Таблица №2
|
1 Трапеция |
2 Трапеция |
||||||||
|
tтабл |
h |
tдейств |
hr0 |
tтабл |
h |
tдейств |
hr0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0,1 |
0,0496 |
0,222222 |
-0,05952 |
0,1 |
0,055 |
0,166667 |
0,165 |
||
|
0,5 |
0,248 |
1,111111 |
-0,2976 |
0,5 |
0,275 |
0,833333 |
0,825 |
||
|
1 |
0,476 |
2,222222 |
-0,5712 |
1 |
0,534 |
1,666667 |
1,602 |
||
|
1,5 |
0,685 |
3,333333 |
-0,822 |
1,5 |
0,758 |
2,5 |
2,274 |
||
|
2 |
0,856 |
4,444444 |
-1,0272 |
2 |
0,938 |
3,333333 |
2,814 |
||
|
2,5 |
0,985 |
5,555556 |
-1,182 |
2,5 |
1,06 |
4,166667 |
3,18 |
||
|
3 |
1,082 |
6,666667 |
-1,2984 |
3 |
1,142 |
5 |
3,426 |
||
|
3,5 |
1,132 |
7,777778 |
-1,3584 |
3,5 |
1,166 |
5,833333 |
3,498 |
||
|
4 |
1,152 |
8,888889 |
-1,3824 |
4 |
1,161 |
6,666667 |
3,483 |
||
|
4,5 |
1,134 |
10 |
-1,3608 |
4,5 |
1,127 |
7,5 |
3,381 |
||
|
5 |
1,115 |
11,11111 |
-1,338 |
5 |
1,069 |
8,333333 |
3,207 |
||
|
5,5 |
1,083 |
12,22222 |
-1,2996 |
5,5 |
1,016 |
9,166667 |
3,048 |
||
|
6 |
1,037 |
13,33333 |
-1,2444 |
6 |
0,956 |
10 |
2,868 |
||
|
6,5 |
1,001 |
14,44444 |
-1,2012 |
6,5 |
0,936 |
10,83333 |
2,808 |
||
|
7 |
0,975 |
15,55556 |
-1,17 |
7 |
0,917 |
11,66667 |
2,751 |
||
|
7,5 |
0,958 |
16,66667 |
-1,1496 |
7,5 |
0,911 |
12,5 |
2,733 |
||
|
8 |
0,951 |
17,77778 |
-1,1412 |
8 |
0,936 |
13,33333 |
2,808 |
||
|
8,5 |
0,949 |
18,88889 |
-1,1388 |
8,5 |
0,958 |
14,16667 |
2,874 |
||
|
9 |
0,96 |
20 |
-1,152 |
9 |
0,99 |
15 |
2,97 |
||
|
9,5 |
0,972 |
21,11111 |
-1,1664 |
9,5 |
1,015 |
15,83333 |
3,045 |
||
|
10 |
0,985 |
22,22222 |
-1,182 |
10 |
1,036 |
16,66667 |
3,108 |
||
|
10,5 |
0,996 |
23,33333 |
-1,1952 |
10,5 |
1,046 |
17,5 |
3,138 |
||
|
11 |
1,002 |
24,44444 |
-1,2024 |
11 |
1,047 |
18,33333 |
3,141 |
||
|
11,5 |
1,006 |
25,55556 |
-1,2072 |
11,5 |
1,043 |
19,16667 |
3,129 |
||
|
12 |
1,006 |
26,66667 |
-1,2072 |
12 |
1,025 |
20 |
3,075 |
||
|
12,5 |
1,006 |
27,77778 |
-1,2072 |
12,5 |
1,01 |
20,83333 |
3,03 |
||
|
13 |
1,006 |
28,88889 |
-1,2072 |
13 |
0,993 |
21,66667 |
2,979 |
||
|
13,5 |
1,006 |
30 |
-1,2072 |
13,5 |
0,982 |
22,5 |
2,946 |
||
|
14 |
1,006 |
31,11111 |
-1,2072 |
14 |
0,974 |
23,33333 |
2,922 |
||
|
14,5 |
1,006 |
32,22222 |
-1,2072 |
14,5 |
0,97 |
24,16667 |
2,91 |
||
|
15 |
1,007 |
33,33333 |
-1,2084 |
15 |
0,976 |
25 |
2,928 |
||
|
15,5 |
1,007 |
34,44444 |
-1,2084 |
15,5 |
0,984 |
25,83333 |
2,952 |
||
|
16 |
1,008 |
35,55556 |
-1,2096 |
16 |
0,993 |
26,66667 |
2,979 |
||
|
16,5 |
1,008 |
36,66667 |
-1,2096 |
16,5 |
1,001 |
27,5 |
3,003 |
||
|
17 |
1,007 |
37,77778 |
-1,2084 |
17 |
1,008 |
28,33333 |
3,024 |
||
|
17,5 |
1,005 |
38,88889 |
-1,206 |
17,5 |
1,012 |
29,16667 |
3,036 |
||
|
18 |
1,002 |
40 |
-1,2024 |
18 |
1,014 |
30 |
3,042 |
||
|
18,5 |
0,999 |
41,11111 |
-1,1988 |
18,5 |
1,012 |
30,83333 |
3,036 |
||
|
19 |
0,995 |
42,22222 |
-1,194 |
19 |
1,009 |
31,66667 |
3,027 |
||
|
19,5 |
0,992 |
43,33333 |
-1,1904 |
19,5 |
1,005 |
32,5 |
3,015 |
||
|
20 |
0,991 |
44,44444 |
-1,1892 |
20 |
1,001 |
33,33333 |
3,003 |
||
|
20,5 |
0,991 |
45,55556 |
-1,1892 |
20,5 |
0,996 |
34,16667 |
2,988 |
||
|
21 |
0,993 |
46,66667 |
-1,1916 |
21 |
0,993 |
35 |
2,979 |
||
|
21,5 |
0,995 |
47,77778 |
-1,194 |
21,5 |
0,992 |
35,83333 |
2,976 |
||
|
22 |
0,996 |
48,88889 |
-1,1952 |
22 |
0,991 |
36,66667 |
2,973 |
||
|
22,5 |
1 |
50 |
-1,2 |
22,5 |
0,992 |
37,5 |
2,976 |
||
|
23 |
1,001 |
51,11111 |
-1,2012 |
23 |
0,994 |
38,33333 |
2,982 |
||
|
23,5 |
1,002 |
52,22222 |
-1,2024 |
23,5 |
0,997 |
39,16667 |
2,991 |
||
|
24 |
1,002 |
53,33333 |
-1,2024 |
24 |
1 |
40 |
3 |
||
|
25 |
1,002 |
55,55556 |
-1,2024 |
25 |
1,003 |
41,66667 |
3,009 |
||
|
26 |
1,002 |
57,77778 |
-1,2024 |
26 |
1,004 |
43,33333 |
3,012 |
||
|
3 Трапеция |
4 Трапеция |
|
|||||||
|
tтабл |
h |
tдейств |
hr0 |
tтабл |
h |
tдейств |
hr0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
0,1 |
0,051 |
0,090909 |
-0,0306 |
0,1 |
0,0384 |
0,02 |
-0,00768 |
|
|
|
0,5 |
0,255 |
0,454545 |
-0,153 |
0,5 |
0,192 |
0,1 |
-0,0384 |
|
|
|
1 |
0,49 |
0,909091 |
-0,294 |
1 |
0,371 |
0,2 |
-0,0742 |
|
|
|
1,5 |
0,706 |
1,363636 |
-0,4236 |
1,5 |
0,538 |
0,3 |
-0,1076 |
|
|
|
2 |
0,878 |
1,818182 |
-0,5268 |
2 |
0,683 |
0,4 |
-0,1366 |
|
|
|
2,5 |
1,01 |
2,272727 |
-0,606 |
2,5 |
0,867 |
0,5 |
-0,1734 |
|
|
|
3 |
1,1 |
2,727273 |
-0,66 |
3 |
0,896 |
0,6 |
-0,1792 |
|
|
|
3,5 |
1,145 |
3,181818 |
-0,687 |
3,5 |
0,963 |
0,7 |
-0,1926 |
|
|
|
4 |
1,158 |
3,636364 |
-0,6948 |
4 |
1,008 |
0,8 |
-0,2016 |
|
|
|
4,5 |
1,134 |
4,090909 |
-0,6804 |
4,5 |
1,029 |
0,9 |
-0,2058 |
|
|
|
5 |
1,107 |
4,545455 |
-0,6642 |
5 |
1,042 |
1 |
-0,2084 |
|
|
|
5,5 |
1,07 |
5 |
-0,642 |
5,5 |
1,046 |
1,1 |
-0,2092 |
|
|
|
6 |
1,021 |
5,454545 |
-0,6126 |
6 |
1,037 |
1,2 |
-0,2074 |
|
|
|
6,5 |
0,982 |
5,909091 |
-0,5892 |
6,5 |
1,03 |
1,3 |
-0,206 |
|
|
|
7 |
0,957 |
6,363636 |
-0,5742 |
7 |
1,024 |
1,4 |
-0,2048 |
|
|
|
7,5 |
0,944 |
6,818182 |
-0,5664 |
7,5 |
1,019 |
1,5 |
-0,2038 |
|
|
|
8 |
0,941 |
7,272727 |
-0,5646 |
8 |
1,02 |
1,6 |
-0,204 |
|
|
|
8,5 |
0,944 |
7,727273 |
-0,5664 |
8,5 |
1,021 |
1,7 |
-0,2042 |
|
|
|
9 |
0,961 |
8,181818 |
-0,5766 |
9 |
1,025 |
1,8 |
-0,205 |
|
|
|
9,5 |
0,98 |
8,636364 |
-0,588 |
9,5 |
1,029 |
1,9 |
-0,2058 |
|
|
|
10 |
0,993 |
9,090909 |
-0,5958 |
10 |
1,031 |
2 |
-0,2062 |
|
|
|
10,5 |
1,007 |
9,545455 |
-0,6042 |
10,5 |
1,033 |
2,1 |
-0,2066 |
|
|
|
11 |
1,014 |
10 |
-0,6084 |
11 |
1,031 |
2,2 |
-0,2062 |
|
|
|
11,5 |
1,017 |
10,45455 |
-0,6102 |
11,5 |
1,028 |
2,3 |
-0,2056 |
|
|
|
12 |
1,019 |
10,90909 |
-0,6114 |
12 |
1,024 |
2,4 |
-0,2048 |
|
|
|
12,5 |
1,018 |
11,36364 |
-0,6108 |
12,5 |
1,019 |
2,5 |
-0,2038 |
|
|
|
13 |
1,014 |
11,81818 |
-0,6084 |
13 |
1,015 |
2,6 |
-0,203 |
|
|
|
13,5 |
1,01 |
12,27273 |
-0,606 |
13,5 |
1,011 |
2,7 |
-0,2022 |
|
|
|
14 |
1,008 |
12,72727 |
-0,6048 |
14 |
1,009 |
2,8 |
-0,2018 |
|
|
|
14,5 |
1,005 |
13,18182 |
-0,603 |
14,5 |
1,008 |
2,9 |
-0,2016 |
|
|
|
15 |
1,002 |
13,63636 |
-0,6012 |
15 |
1,007 |
3 |
-0,2014 |
|
|
|
15,5 |
1,001 |
14,09091 |
-0,6006 |
15,5 |
1,006 |
3,1 |
-0,2012 |
|
|
|
16 |
1 |
14,54545 |
-0,6 |
16 |
1,006 |
3,2 |
-0,2012 |
|
|
|
16,5 |
1,001 |
15 |
-0,6006 |
16,5 |
1,005 |
3,3 |
-0,201 |
|
|
|
17 |
0,999 |
15,45455 |
-0,5994 |
17 |
1,005 |
3,4 |
-0,201 |
|
|
|
17,5 |
0,997 |
15,90909 |
-0,5982 |
17,5 |
1,003 |
3,5 |
-0,2006 |
|
|
|
18 |
0,997 |
16,36364 |
-0,5982 |
18 |
1,002 |
3,6 |
-0,2004 |
|
|
|
18,5 |
0,995 |
16,81818 |
-0,597 |
18,5 |
1,001 |
3,7 |
-0,2002 |
|
|
|
19 |
0,993 |
17,27273 |
-0,5958 |
19 |
0,998 |
3,8 |
-0,1996 |
|
|
|
19,5 |
0,992 |
17,72727 |
-0,5952 |
19,5 |
0,996 |
3,9 |
-0,1992 |
|
|
|
20 |
0,992 |
18,18182 |
-0,5952 |
20 |
0,995 |
4 |
-0,199 |
|
|
|
20,5 |
0,994 |
18,63636 |
-0,5964 |
20,5 |
0,994 |
4,1 |
-0,1988 |
|
|
|
21 |
0,997 |
19,09091 |
-0,5982 |
21 |
0,994 |
4,2 |
-0,1988 |
|
|
|
21,5 |
1 |
19,54545 |
-0,6 |
21,5 |
0,995 |
4,3 |
-0,199 |
|
|
|
22 |
1 |
20 |
-0,6 |
22 |
0,995 |
4,4 |
-0,199 |
|
|
|
22,5 |
1,004 |
20,45455 |
-0,6024 |
22,5 |
0,996 |
4,5 |
-0,1992 |
|
|
|
23 |
1,006 |
20,90909 |
-0,6036 |
23 |
0,996 |
4,6 |
-0,1992 |
|
|
|
23,5 |
1,007 |
21,36364 |
-0,6042 |
23,5 |
0,996 |
4,7 |
-0,1992 |
|
|
|
24 |
1,008 |
21,81818 |
-0,6048 |
24 |
0,996 |
4,8 |
-0,1992 |
|
|
|
24,5 |
1,006 |
22,27273 |
-0,6036 |
24,5 |
0,996 |
4,9 |
-0,1992 |
|
|
|
25 |
1,004 |
22,72727 |
-0,6024 |
25 |
0,995 |
5 |
-0,199 |
|
|
|
25,5 |
1,002 |
23,18182 |
-0,6012 |
25,5 |
0,995 |
5,1 |
-0,199 |
|
|
|
26 |
1 |
23,63636 |
-0,6 |
26 |
0,995 |
5,2 |
-0,199 |
|
|