Метод Гаусса-Зейделя

В отличие от метода Якоби, в котором вычисления всех компонент вектора -го приближения проводилось однообразно, в методе Гаусса-Зейделя для расчета -й компоненты следующего приближения используется уже вычисленное на этом, т.е. -м шаге, новые значения первых компонент:

Или, в компактном виде:

, i=1, 2, …, m. (2.12)

_{Достаточное условие сходимости этого метода, как и для методы Якоби, является условие диагонального преобладания:}

, .

_{ПРИМЕР 2.6. Найдем решение СЛАУ из Примера 2.4 методом Гаусса-Зейделя.}

.

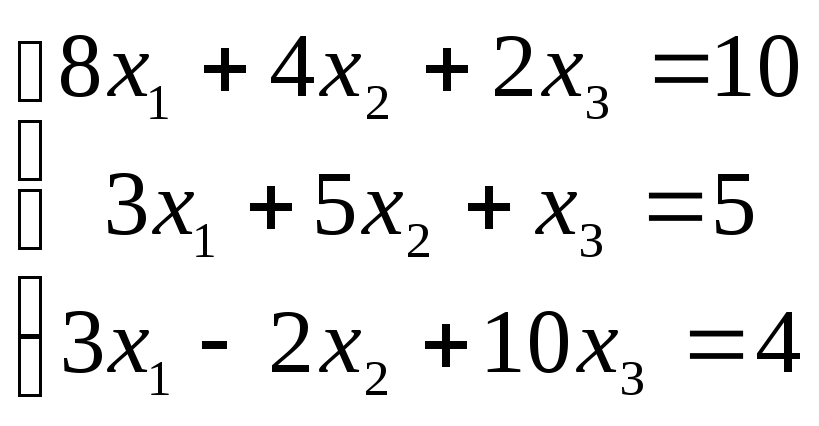Расчетные формулы:

.

Таблица итераций выглядит в данном случае следующим образом:

Номер итерации
0	0	0	0
1	1.25	0.25	0.075	1.25
2	1.10625	0.32125	0.132375	0.14375
3	1.056281	0.339756	0.151067	0.049969
4	1.042355	0.344374	0.156168	0.013926
5	1.038771	0.345504	0.157469	0.003584

Здесь

,

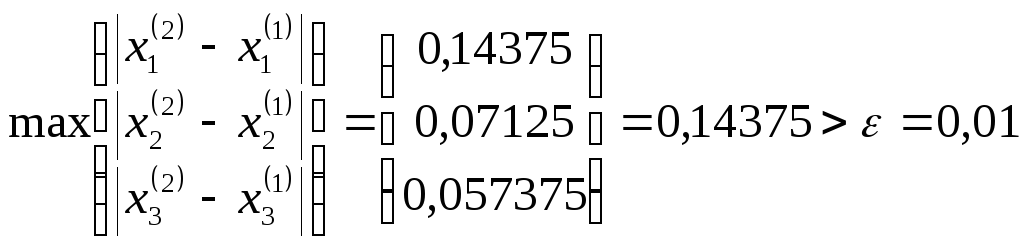, и т.д.

Из таблицы видно, что нужная точность достигнута уже на 5-ой итерации вместо 11-ой по методу простой итерации.

При реализации в Excel расчетные формулы для примут вид: =1/$B$1*($G$1-$C$1*C6-$D$1*D6),

=1/$C$2*($G$2-$B$2*B7-$D$2*D6), =1/$D$3*($G$3-$B$3*B7-$C$3*C7).

Аппроксимация функций

Слово «аппроксимация» происходит от латинского approximo — приближаюсь. Аппроксимировать – это означает приближенно заменить. Задачи интерполяции возникают при обработке результатов экспериментов, когда измерения какой-либо величины выполнены в конечном числе точек. Требуется найти промежуточные значения этой функции. Это так называемая задача о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять (аппроксимировать) алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции). Методы интерполяции используются для приближенного интегрирования и решения дифференциальных уравнений, а также являются основой компьютерной графики и других современных цифровых технологий.

Постановка задачи интерполяции

На интервале заданы точки , ; , и значения неизвестной функции в этих точках , . Требуется найти функцию , принимающую в точках те же значения . Точки будем называть узлами интерполяции, а условия  – условиями интерполяции. При этом будем искать только на отрезке . Если необходимо найти функцию вне отрезка, то такая задача называется задачей экстраполяции. Мы будем рассматривать только задачи интерполяции.

Поставленная задача имеет много решений, т.к. через заданные точки , , можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай аппроксимации функции многочленами, т.е. , где – постоянные коэффициенты.

Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале строится отдельный полином. В случае глобальной интерполяции отыскивается единый полином на всем интервале . При этом искомый полином называется интерполяционный полиномом.