1.4. Выбор частоты квантования и восстановление сигналов по дискретным выборкам

Теорема Шеннона. Квантование непрерывного процесса всегда сопровождается потерей информации. При этом очевидно, что если моменты квантования следуют достаточно часто, то потери информации незначительны и наоборот. Таким образом, при проектировании дискретных систем частоту квантования следует выбирать как можно более высокой. С другой стороны, интуитивно ясно, что потеря информации при квантовании зависит и от частотного спектра преобразуемого процесса. Так, например, квантование с любой частотой постоянного сигнала не ведет к потере информации, в то время как при квантовании процесса с высокочастотной составляющей потеря информации будет зависеть от соотношения частоты квантования и частоты этой составляющей. Таким образом, поскольку реальные процессы всегда содержат ограниченный спектр частот, то беспредельное увеличение частоты квантования является нецелесообразным.

Приводимая ниже теорема, которая носит название теоремы Шенона, устанавливает условия, при которых непрерывный процесс однозначно определяется своими дискретами.

Теорема. Непрерывный сигнал, преобразование Фурье которого равно нулю вне интервала, однозначно представляется своими значениями в равноотстоящих точках, если частота квантования. При этом непрерывный сигнал может быть получен из дискретного по формуле

. (1.4.1)

Для доказательства теоремы предположим, что - некоторый непрерывный процесс, а- его преобразование Фурье, то есть

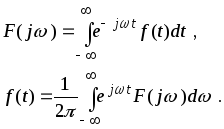(1.4.2)

Введем вспомогательную функцию

, (1.4.3)

которая по построению является периодической относительнос периодом, и следовательно, может быть разложена в ряд Фурье

, (1.4.4)

где - коэффициенты этого ряда, вычисляемые по формуле[4].

. (1.4.5)

Используя (1.4.3) это выражение можно записать в виде

.

Нетрудно увидеть, что выражение в фигурных скобках, представляющее собой бесконечную сумму собственных интегралов с конечными пределами, превращается в несобственный интеграл с бесконечными пределами. Таким образом (1.4.5) преобразуется к виду

.

Сравнивая это выражение с обратным преобразованием Фурье (1.4.2), заключаем, что , и тогда (1.4.4) принимает вид

. (1.4.6)

Отсюда следует, что квантованный сигнал однозначно определяет функцию, которую можно рассматривать как дискретное преобразование Фурье от дискретной функции.

Пусть в соответствии с условиями теоремы , причем, при. Тогда из (1.4.3) вытекает

. (1.4.7)

Графически эта связь представлена на рис.1.7, где показана зависимость от частоты модуля некоторой функции , и жирной линией выделено ее совпадение в диапазоне частотс функцией.

Таким образом, если выполняются условия теоремы, то преобразование Фурье непрерывного сигнала (а, следовательно, и сам сигнал) однозначно представляется функцией, которая в свою очередь определяется дискретной функцией, что и доказывает первую часть теоремы.

Рис. 1.7.

Для доказательства формулы (1.4.1) используем условие (1.4.7), и, применяя обратное преобразование Фурье, запишем для непрерывной функции с учетом (1.4.6) следующее соотношение

.

Меняя порядок интегрирования и суммирования, будем иметь

.

Откуда, учитывая, что , окончательно получаем формулу (1.4.1), завершая тем самым доказательство теоремы.

Из приведенной теоремы вытекает, что если непрерывный сигнал квантуется с частотой, где- граничная частота частотного спектра сигнала, то квантование будет происходить без потери информации (речь идет лишь о квантовании по времени), так как этот сигнал может быть снова восстановлен по своим дискретам.

Восстановление непрерывного процесса методом экстраполяции. Формальное восстановление непрерывного сигнала по его дискретным значениям может быть осуществлено с помощью формулы (1.4.1). Такой способ получил название восстановление Шенона. Следует, однако, заметить, что восстановление Шенона не является причинно-следственным, так как значение непрерывного сигнала в моментвыражается как через предшествующее, так и через последующиедискреты. В связи с этим в задачах непрерывно-дискретного управления, например, при цифро-аналоговом преобразовании дискретного управляющего воздействияв непрерывный процесс, восстановление Шеннона неприемлемо, так как здесь мы имеем дискретытолько до текущего момента, т.е. при. Кроме того, сама формула (1.4.1) является достаточно сложной для ее практического использования. По этой причине, в системах управления с БЦВМ в контуре для восстановления непрерывного управленияпо его дискретам обычно применяют метод экстраполяции, то есть нахождение функциина интервалепо известным значениям этой функции в текущий моменти в предшествующие моменты.

Очевидно, что наиболее точное воспроизведение функции по ее значениямможно получить, если на интервале между моментами квантованияивоспользоваться разложением этой функции в степенной ряд, то есть

(1.4.8)

где

. (1.4.9)

Реализация управления по формуле (1.4.8), в которой число членов ряда ограничено величиной, где- старшая степень ряда, называется экстраполяцией- го порядка.

Очевидно, что точность восстановления зависит от точности вычисления коэффициентов ряда по формулам (1.4.9). Однако, поскольку информация о функциидоступна только для дискретных моментов, то эти коэффициенты можно вычислить лишь приближенно.

Рассмотрим алгоритм вычисления производных (1.4.9) для восстановления управления с помощью экстраполяции-го порядка. В этом случае (1.4.8) принимает вид

(1.4.10)

Запишем это выражение для моментов времени .

В результате получим

(1.4.11)

Считая для простоты, что управление является скалярной переменной, введеммерные векторы

(1.4.12)

Тогда систему равенств (1.4.11) можно записать в векторно-матричной форме

, (1.4.13)

где -- матрица, составленная из коэффициентов уравнений (1.4.11), и определяемая следующим выражением

. (1.4.14)

По построению эта матрица является неособой. Причем можно показать, что абсолютное значение ее определителя

. (1.4.15)

Таким образом из (1.4.13) вытекает алгоритм определения производных , как компонент вспомогательного вектора, то есть

. (1.4.16)

Из этой формулы, с учетом структуры вектора , можно заключить, что для восстановленияс помощью экстраполяции- го порядка необходимо, помимо дискреты, иметь ещепредшествующих значенийвосстанавливаемого процесса, что по существу, эквивалентно введению в контур регулирования временных запаздываний по управлению натактов одновременно. Известно[3], что запаздывание всегда отрицательно сказывается на процессы, протекающие в замкнутой системе. Поэтому, при восстановлении управляющих сигналов обычно ограничиваются экстраполяцией нулевого порядка, т.е. применяют восстановление с фиксацией на период. В этом случае, при, и восстановленный процесс представляется кусочно-постоянной функцией. Ошибка такого восстановления может быть оценена[7]по формуле

.

Иногда используется экстраполяция первого порядка. Тогда в соответствии с (1.4.10), (1.4.16) будем иметь

и можно показать [7], что ошибка восстановления в этом случае удовлетворяет условию

.

Экстраполяция 2-го и более высоких порядков практически не используется в связи с тем, что выигрыш в точности восстановления оказывается несущественным по сравнению с тем отрицательным эффектом, который начинает проявляться из-за наличия запаздывания по управлению. Что касается возможности использования экстраполяции выше первого порядка при малых периодах дискретности, когда запаздывание оказывается несущественным, то здесь надо отметить следующее. Из (1.4.15) следует, что при малых и даже при относительно небольшихматрица, определяемая выражением (1.4.14), близка к вырожденной. Это означает, что в этом случае возникает проблема с определением производных, входящих в (1.4.10). Этот факт является косвенным подтверждением того, что при малыхиспользование экстраполяции 2-го и более высоких порядков является нерациональным.

18