[Править] Глобальные

• Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.

• Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.

• Областью значений функции , непрерывной на отрезке 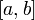, является отрезок  где минимум и максимум берутся по отрезку .

• Если функция  непрерывна на отрезке  и  то существует точка  в которой .

• Если функция  непрерывна на отрезке  и число  удовлетворяет неравенству  или неравенству  то существует точка  в которой .

• Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.

• Монотонная функция на отрезке  непрерывна в том и только в том случае, когда область ее значений является отрезком с концам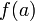и  и .

• Если функции  и  непрерывны на отрезке , причем  и  то существует точка  в которой  Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.

9. Бесконечно малые. Сравнение бескол.

10. Производная сложная и геометрический смысл.

Пусть функция    определена в точке    и некоторой ее окрестности. Придадим аргументуприращение  такое, что точка  попадает в область определения функции.  Функция при этом получит приращение  . 

     ОПРЕДЕЛЕНИЕ 1. Производной функции    в точке  называется предел отношения приращения функции в этой точке к приращению аргумента ,  при (если этот предел существует и конечен), т.е.

11. .

Обозначают: .

Производной функции  в точке справа (слева) называется

(если этот предел существует и конечен).

Обозначают:   – производная y=f(x)  в точкесправа,

  – производная y=f(x) в точкеслева.

 

Очевидно, что справедлива следующая теорема.

    Теорема 1: Функция y=f(x) имеет производную в точкетогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева. Причем

.

Следующая теорема устанавливает связь между существованием производной функции в точке и непрерывностью функции в этой точке.

ТЕОРЕМА (необходимое условие существования производной функции в точке).  Если функция  y = f(x) имеет производную в точке, то функция f(x)  в этой точке непрерывна.

ДОКАЗАТЕЛЬСТВО

Пусть существует  .  Тогда

,

где – бесконечно малая при .

⇒  ;

⇒  

.

Но это означает, что функция f(x) непрерывна в точке   (по геометрическому определению непрерывности). ∎

11. Свойства производных.

12. Производные элементарной функции.

13. Дифференцирование функции.

14. Дифференциал.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х.                                             (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

dy=ƒ'(х)dх,                                              (24.2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение

производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.