
- •Вопросы по математическому анализу
- •Основные свойства пределов.
- •Непрерывность функции в точке.
- •Свойства непрерывных функций.
- •Локальные
- •[Править] Глобальные
- •Производная сложная и геометрический смысл.
- •Дифференциал.
- •Исследование функции.
- •1) Отыскивается область определения функции.
- •3) Находим точки пересечения графика функции с осями координат.
- •5) Ищутся асимптоты графика функции.
- •6) Находятся критические точки и интервалы монотонности.
- •7) Ищутся точки перегиба и интервалы выпуклости.
- •Необходимое условие.
- •17.Достаточное условие.
- •1) Первое достаточное условие:
- •2) Второе достаточное условие
- •3) Третье достаточное условие
-
Свойства непрерывных функций.
Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения.
|
Теорема
1.
Сумма непрерывных функций есть функция
непрерывная.
Доказательство.
Пусть функции
Согласно
свойству пределов функций существование
пределов функций
что и требовалось доказать. Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная. Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция. Теорема 2. Произведение непрерывных функций есть функция непрерывная. Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль. Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю. Теорема
4.
Любая элементарная функция непрерывна
в области своего определения.
Для
доказательства этой теоремы нужно
показать, что для любого числа a
из области определения элементарной
функции
Продемонстрируем справедливость теоремы на некоторых конкретных примерах.
Первый член в правой части этого равенства представляет собой бесконечно малую функцию при x → a и, следовательно,
Теорема
5.
Пусть функция |
|
|
Локальные
-
Функция, непрерывная в точке
 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки. -
Если функция
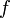 непрерывна
в точке
непрерывна
в точке  и
и  (или
(или  ),
то
),
то  (или
(или  )
для всех
)
для всех  ,
достаточно близких к
,
достаточно близких к  .
. -
Если функции
 и
и  непрерывны
в точке
непрерывны
в точке  ,
то функции
,
то функции  и
и  тоже
непрерывны в точке
тоже
непрерывны в точке  .
. -
Если функции
 и
и  непрерывны
в точке
непрерывны
в точке  и
при этом
и
при этом  ,
то функция
,
то функция  тоже
непрерывна в точке
тоже
непрерывна в точке  .
. -
Если функция
 непрерывна
в точке
непрерывна
в точке 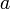 и
функция
и
функция  непрерывна
в точке
непрерывна
в точке  ,
то их композиция
,
то их композиция  непрерывна
в точке
непрерывна
в точке  .
.
