
- •Вопросы по математическому анализу
- •Основные свойства пределов.
- •Непрерывность функции в точке.
- •Свойства непрерывных функций.
- •Локальные
- •[Править] Глобальные
- •Производная сложная и геометрический смысл.
- •Дифференциал.
- •Исследование функции.
- •1) Отыскивается область определения функции.
- •3) Находим точки пересечения графика функции с осями координат.
- •5) Ищутся асимптоты графика функции.
- •6) Находятся критические точки и интервалы монотонности.
- •7) Ищутся точки перегиба и интервалы выпуклости.
- •Необходимое условие.
- •17.Достаточное условие.
- •1) Первое достаточное условие:
- •2) Второе достаточное условие
- •3) Третье достаточное условие
Вопросы по математическому анализу
-
Предел функции. Функция стремится к бесконечности.
-
Основные свойства пределов.
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
![]()
Расширенное правило суммы
![]()
Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
![]()
Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
![]()
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
![]()
Расширенное правило произведения
![]()
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
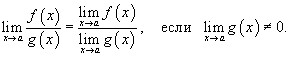
Предел степенной функции
![]()
где степень p - действительное число. В частности,
![]()
Если f ( x ) = x, то
![]()
Предел показательной функции
![]()
где основание a > 0.
Предел логарифмической функции
![]()
где основание a > 0.
Теорема "о двух милиционерах"
Предположим,
что ![]() для
всех x близких
к a,
за исключением, быть может, самой точкиx
= a.
Тогда, если
для
всех x близких
к a,
за исключением, быть может, самой точкиx
= a.
Тогда, если
![]()
то
![]()
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу L.
-
Предел функции sin x/x
-
Предел (1 + 1/n) ^ n
-
Непрерывность функции в точке.
1.
Функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
если пределы слева и справа равны и
равны значению функции в этой точке, т.
е.
,
если пределы слева и справа равны и
равны значению функции в этой точке, т.
е.
![]()
2.
Функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
если она определена в этой точке и если
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции, т. е.
,
если она определена в этой точке и если
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции, т. е. ![]() вблизи
точки
вблизи
точки ![]() .
.
Сумма, разность и произведение конечного числа непрерывных функций есть функция непрерывная.
Непрерывная
на отрезке ![]() функция
принимает любое промежуточное значение
между ее наименьшим
функция
принимает любое промежуточное значение
между ее наименьшим ![]() и
наибольшим
и
наибольшим ![]() значением,
то есть
значением,
то есть ![]() для
всех
для
всех ![]() .
Отсюда следует, что если в граничных
точках отрезка
.
Отсюда следует, что если в граничных
точках отрезка ![]() функция
имеет разные знаки, то внутри отрезка
есть по крайней мере одно такое значение
функция
имеет разные знаки, то внутри отрезка
есть по крайней мере одно такое значение ![]() ,
при котором функция обращается в ноль.
Это свойство непрерывности функций
позволяет находить приближенно корни
многочленов.
,
при котором функция обращается в ноль.
Это свойство непрерывности функций
позволяет находить приближенно корни
многочленов.
Теоремы непрерывности
Теорема
1.
Пусть
функция f (x) непрерывна
в точке x
= a,
и C является
константой. Тогда функция Сf (x) также
непрерывна при x
= a.
Теорема
2.
Даны
две функции f (x) и g (x),
непрерывные в точке x
= a.
Тогда сумма этих функций f (x)
+ g (x) также
непрерывна в точке x
= a.
Теорема
3.
Предположим,
что две функции f (x) и g (x) непрерывны
в точке x
= a.
Тогда произведение этих функцийf (x) g (x) также
непрерывно в точке x
= a.
Теорема
4.
Даны
две функции f (x) и g (x),
непрерывные при x
= a.
Тогда отношение этих функций ![]() также
непрерывно при x
= a при
условии, что
также
непрерывно при x
= a при
условии, что ![]() .
Теорема
5.
Предположим,
что функция f (x) является
дифференцируемой в точке x
= a.
Тогда функция f (x) непрерывна
в этой точке (т.е. из дифференцируемости
следует непрерывность функции в точке;
обратное − неверно).
Теорема
6 (Теорема о предельном значении).
Если
функция f (x) непрерывна
на закрытом и ограниченном интервале [a,
b],
то она ограничена сверху и снизу на
данном интервале. Другими словами,
существуют числа m и M,
такие, что
.
Теорема
5.
Предположим,
что функция f (x) является
дифференцируемой в точке x
= a.
Тогда функция f (x) непрерывна
в этой точке (т.е. из дифференцируемости
следует непрерывность функции в точке;
обратное − неверно).
Теорема
6 (Теорема о предельном значении).
Если
функция f (x) непрерывна
на закрытом и ограниченном интервале [a,
b],
то она ограничена сверху и снизу на
данном интервале. Другими словами,
существуют числа m и M,
такие, что
![]()
для всех x в интервале [a, b] (смотрите рисунок 1).
-
Непрерывность функции на интервале.
-
Точки разрыва.
Определение. Функция ![]() имеет точку
разрыва при
имеет точку
разрыва при ![]() ,
если она определена слева и справа от
точки
,
если она определена слева и справа от
точки ![]() ,
но в точке
,
но в точке ![]() не
выполняется хотя бы одно из условий
непрерывности.
не
выполняется хотя бы одно из условий
непрерывности.
Точки
разрыва функции ![]() :
:
-
Точка устранимого разрыва;
-
Точка разрыва первого рода;
-
Точка разрыва второго рода.
Точка ![]() является точкой
устранимого разрыва,
если функция в точке
является точкой
устранимого разрыва,
если функция в точке ![]() не
определена и существуют равные конечные
пределы
не
определена и существуют равные конечные
пределы ![]() и
и ![]() ,
т.е.
,
т.е.![]() .
.
Точка ![]() является точкой
разрыва первого рода,
если существуют конечные пределы
является точкой
разрыва первого рода,
если существуют конечные пределы![]() и
и ![]() ,
т.е. выполняется второе условие
непрерывности и не выполняются остальные
условия или хотя бы одно из них.
,
т.е. выполняется второе условие
непрерывности и не выполняются остальные
условия или хотя бы одно из них.
Точка ![]() является точкой
разрыва второго рода,
если один из пределов
является точкой
разрыва второго рода,
если один из пределов ![]() и
и![]() равен
бесконечности (
равен
бесконечности (![]() ).
).
