Математическое моделирование движения иглы в замке вязального механизма на эвм

Математическая модель (5) движения иглы в замке вязального механизма представляет собой нелинейное дифференциальное уравнение второго порядка. Для решения математической модели (5), с учетом (1), (6), (7) и (8) воспользуемся численным методом Рунге-Кутта ΙV, предварительно воспользовавшись заменой

, ,

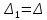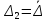приведем (5) к каноническому виду

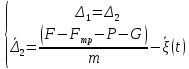, (16)

при t=0 .

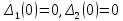Для решения математической модели на ЭВМ воспользуемся системой инженерных и научных расчетов MATLAB [4] и входящей в нее функцией ode45( ), предназначенной для решения дифференциальных уравнений методом Рунге-Кутта четвертого и пятого порядка с автоматическим выбором шага интегрирования. Обращение к функции ode45( ) в программе на языке программирования системы MATLAB имеет вид

[t,Y]=ode45(@fundydt,[t0,tk],y0);

где выходные параметры:

@fundydt – имя функции, в которой вычисляются правые части системы дифференциальных уравнений, записанных в каноническом виде;

[t0,tk] – интервал времени, на котором производится инегрирование системы дифференциальных уравнений;

y0 – вектор начальных условий;

выходные параметры:

t – вектор-строка, содержащая моменты времени, соответствующие решению Y;

Y – выходной массив, каждая строка которого соответствует решению дифференциальных уравнений в моменты времени t.

Данная программа состоит из головного модуля и трех подпрограмм – функций ksi( ), sila( ), sysdif( ).

Блок-схема работы данной программы представлена на рисунке 7. В головном модуле происходит ввод исходных данных, решение дифференциального уравнения математической модели, расчет значений и построение графиков зависимостей .

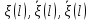Подпрограмма ksi( ) вычисляет зависимости 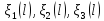и их первой и второй передаточных функций соответственно на участках Ι, ΙΙ, ΙΙΙ по зависимостям, определенным в результате синтеза профиля клиньев замка. Длины l₁, l₂, l₃ соответствующих участков вычисляются в головном модуле после задания исходных данных.

Подпрограмма sila( ) вычисляет значения сил F, F_тр и Р в функции времени t и обобщенных координат .

Подпрограмма sysdif( ) вычисляет правые части системы дифференциальных уравнений (16).

Описание графиков

По результатам работы программы, представленной в «Приложении Д», были представлены графики положения, сил и деформаций иглы в замке вязального механизма.

На рисунке 1 представлены графики функции положения, первой и второй передаточной функций. Данные графики описывают зависимость перемещения, скорости и ускорения от длины участка.

Первый график представляет собой функцию положения 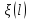. Единицы измерения на данном графике для длины L и перемещения ξ – м. Движение начинается из точки z=0 м и заканчивается в точке z=0,014. На Ι участке закон движения – парабола, на ΙΙ – прямая, на ΙΙΙ – синусоида. Стыки между Ι и ΙΙ, ΙΙ и ΙΙΙ участками плавные, скачков нет.

Второй график – это первая передаточная функция 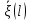или скорость. На данном графике единицы измерения скорости – м/с, длины – м. Движение начинается из точки со значением 0. Ι участок: прямая, скорость изменяется по линейному закону от 0 до 0,8. Переход на второй участок излом. На ΙΙ участке прямая, что означает что скорость постоянная. Переход на третий участок плавный. На ΙΙΙ участке – косинусоида. Скорсть меняется по закону косинусоиды от 0,8 до 0.

Третий график – вторая передаточная функция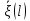 или ускорение.

На участке Ι прямая. Ускорение постоянное и равно 160 м/с². Переход на второй участок – скачёк. ΙΙ участок прямая. Ускорение равно 0. Переход на третий участок – скачёк. На ΙΙΙ участке изображена синусоида. Максимальное ускорение на данном участке равно -160 м/с².

Стык между Ι и ΙΙ, ΙΙ и ΙΙΙ участками в виде излома. Это свидетельствует о мягком ударе.

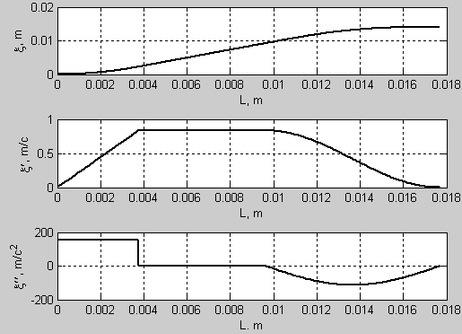
Рисунок 1 – графики функции положения, первой и второй передаточной функций

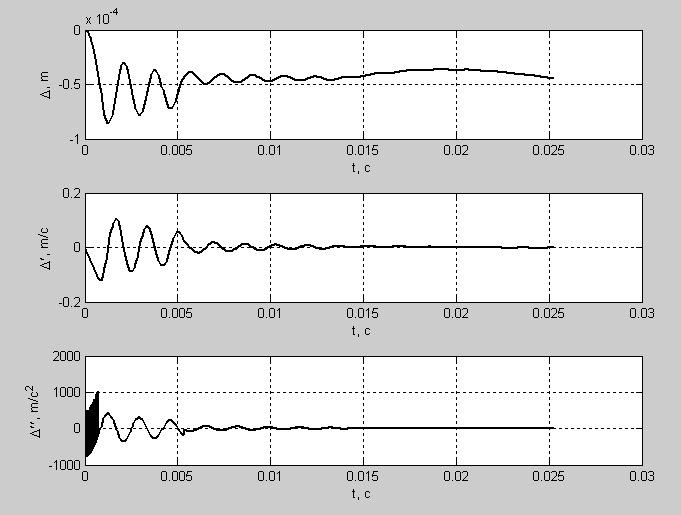
На рисунке 2 изображены графики затухающих гармонических колебаний, представляющих собой деформацию Δ, ее скорость Δ′ и ускорение Δ′′.

На первом графике деформация начинается из точки 0 до -0,4*10^-4 м, с максимальной амплитудой равной 0,7*10^-4. Затем переходит в затухающие гармонические колебания.

На втором графике представлена скорость деформации. Из начального положения, равного 0 м, скорость деформации изменяется линейно, доходя до максимума в точке 0,11 м/с. После этого скорость изменяется в виде затухающих гармонических колебаний переходя в нулевое значение.

Ускорение деформации на третьем графике изначально колеблется между максимальным и минимальным значениями, которые равны -650 м/с² и 800 м/с². Это происходит за время, равное 0,0008 с, и соответствует движению в зазоре или виброудару. После этого начинаются затухающие колебания, с небольшим изломом вначале, который описывает мягкий удар.

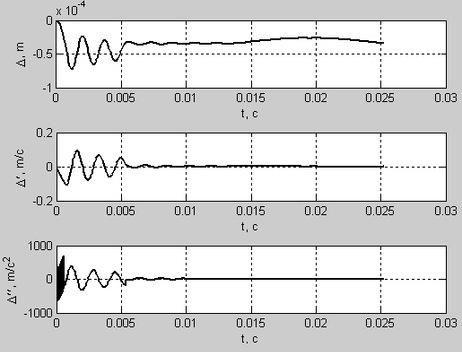
Рисунок 2 – графики деформации

На рисунке 10 представлены графики силы трения F_тр, силы полезного сопротивления P, и силы, действующей со стороны замка на иглу. Все силы имеют размерность Н.

На первом графике сила трения колеблется от –0,21 Н до 0,21 Н. Это свидетельствует о том, что в данном месте зона зазора. Со времени t=0,0007 с сила трения постоянна и равна –0,21 Н, скорость убывает в данном случае.

Сила полезного сопротивления, представленная на втором графике, попадает в зазор и колеблется там от –0,1 Н до 0,1 Н. При значении времени t=0,0003 с сила сопротивления становится постоянной и равной –0,1 Н.

На третьем графике сила действовет по гармоническому закону затухающих колебаний. С максимальной амплитудой от 0 до 0,25.

ΙΙ и ΙΙΙ участок – зеркальное отображение графика деформации

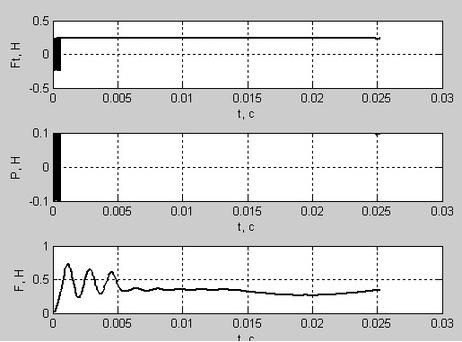
Рисунок 3 – графики сил

При увеличении усилия полезного сопротивления в два раза происходят изменения предоставленные на следующем графике

При увеличение Силы в 2 раза произошли изменения на графике ускорения деформации. Максимальная амплитуда увеличилась в 0,8 раз и колебаний до полной остановки стало больше.