2 Анализ нелинейной системы

2.1 Преобразование структурной схемы нелинейной системы управления вала дизеля

В систему, представленную на рисунке 8, введен нелинейный элемент, имеющий статическую характеристику вида:

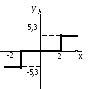
Рисунок 8 – Характеристика нелинейного элемента с зоной нечувствительности

Статическая характеристика нелинейного элемента описывается следующей системой уравнений:

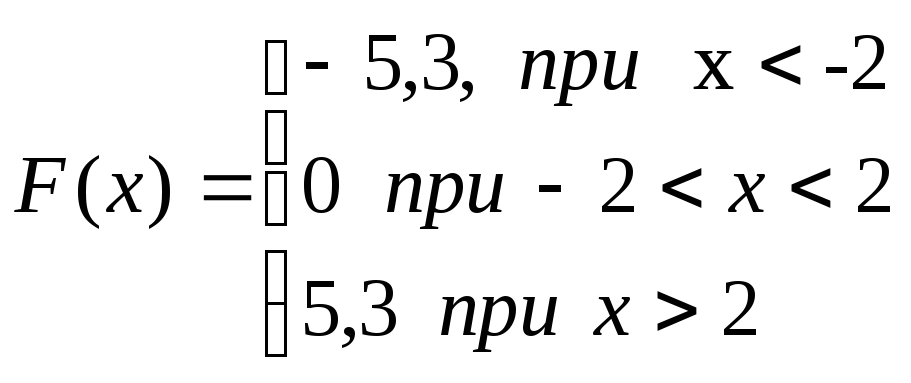
Для исследования нелинейных систем функциональную схему, а, следовательно и структурную схему преобразовывают так, чтобы получить простейшую одноконтурную систему, в которой нелинейный элемент и линейная часть были бы соединены последовательно.

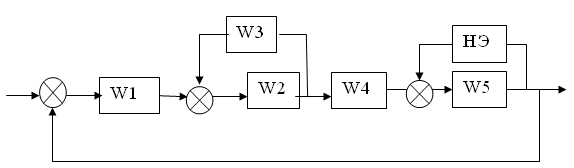
Рисунок 9 – Функциональная схема линейной системы управления вала дизеля с нелинейным элементом

Для построения фазового портрета упростим структурную схему нелинейной системы управления.

Найдем общую передаточную функцию линейной системы, для этого преобразуем в соответствии с правилами преобразования, для этого разобьем структурную схему на участки:

- передаточная функция 1 участка:

;

- передаточная функция 2 участка:

;

- передаточная функция 4 участка является общей передаточной функцией линейной части системы:

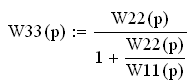
Тогда структурная схема линейной системы с выделенным нелинейным элементом имеет вид:

Рисунок 10 – Преобразованная схема нелинейной системы вала дизеля

Передаточная функция линейной части системы примет вид:

;

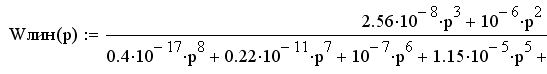
2.2 Расчет нелинейной системы методом фазовых траекторий

Для расчета нелинейной системы методом фазовых траекторий характеристическое уравнение передаточной функции линейной части не должно превышать второго порядка. С учетом этого передаточная функция линейной части:

Предположим, что задающее воздействие , тогда уравнение нелинейной САУ будет иметь вид:

Характеристика нелинейного элемента разбивается на 3 участка и для каждого из них составляется линейное дифференциальное уравнение:

1 участок:

, если

, если

2 участок:

, если

, если

3 участок:

, если

Для фазовой плоскости введем обычные координаты и . Тогда линейные уравнения для этих участков примут вид:

1 участок:

, если

2 участок:

, если

3 участок:

, если

В Mathcad программа получения фазовых траекторий на фазовой плоскости путем непосредственного решения линейных дифференциальных уравнений

будет иметь вид:

- зададим значения коэффициентов:

k=1;

b=2;

c=5.3;

T₁=0.27;

T₂=1.

- зададим начальные значения для векторов , , :

,

,

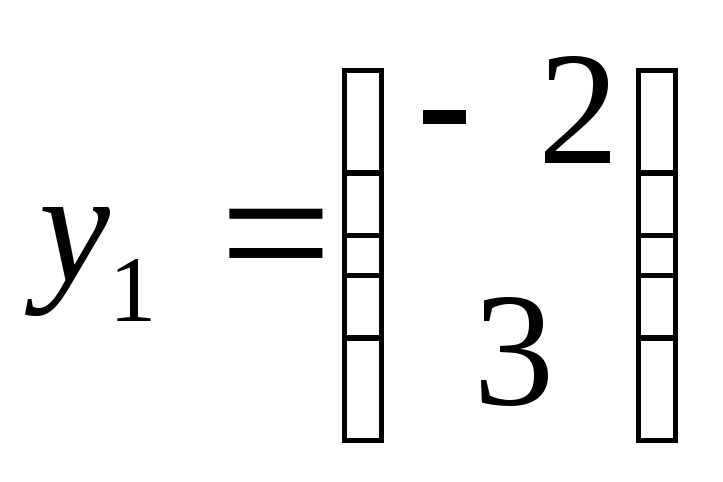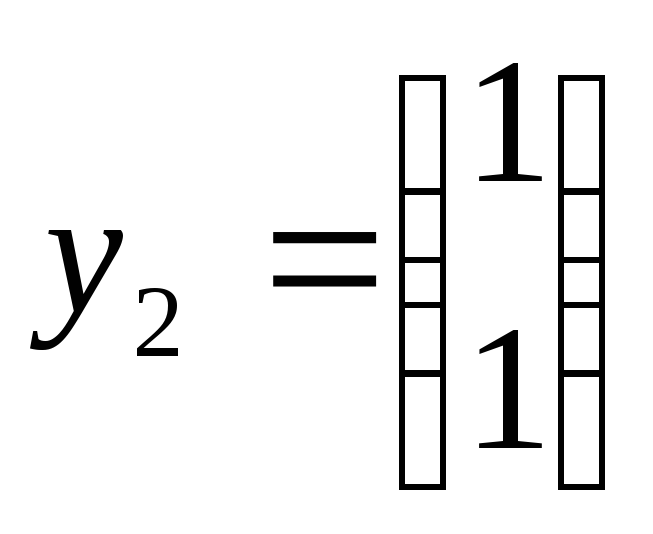
Определяем функцию по трем линейным участкам нелинейной статической характеристики, задающую производную:

;

- найдем матрицы решений для различных начальных условий:

- построим траектории на фазовой плоскости, предполагая, что первые столбцы матриц решения , , содержат точки, в которых ищется решение дифференциального уравнения, вторые - , , - содержат значения найденного решения, то есть , , и, наконец, третьи столбцы , , содер-

жат первые производные этого решения, то есть , , .

Приведем фазовые траектории и переходные процессы при различных начальных условиях:

;

;

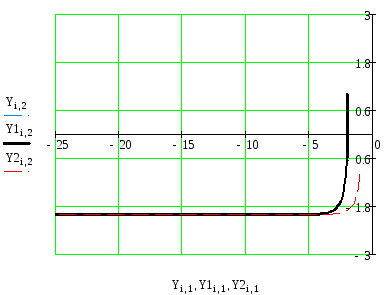
Рисунок 11 - Фазовый портрет для выходных координат

По виду фазового портрета, представленного на рисунке 11, можно утверждать, что исследуемая нелинейная система является неадекватной.

Заключение

Цель данной курсовой работы состояла в исследовании и анализе системы автоматического управления вала мощного дизеля в различных её состояниях: линейная система и нелинейная система.

Анализ линейной системы показал, что она является устойчивой, поскольку переходный процесс приходит в установившееся состояние, а также по критерию Гурвица - система устойчива. Но при исследовании переходного процесса прямая оценка качества δ-перерегулирование, равная 0 %, показала, что система является неадекватной. С введением в нее нелинейного элемента её фазовый портрет подтвердил это заключение. Система требует программной коррекции.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1 Основы теории автоматического регулирования: Учебник для машиностроительных специальных вузов/ В.И. Крутов, Ф. М. Данилов, П. К. Кузьмин и др.; Под ред. В. И. Крутова. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1984. - 368 с.: ил.

2 Теория автоматического управления/ Под ред. А.В. Нетушила. – М.: Высшая школа, 1977. – 519 с.: ил.

3 Основы автоматического регулирования/ Под ред. В.С. Пугачева. – М.: Наука, 1974. – 720 с.: ил.

4 Самоучитель MathCad 11 Кирьянов Д.В.. – СПб.: БХВ – Петербург, 2003. – 560с

5 Исследование САУ на фазовой плоскости: Методические указания к лабораторной работе по курсу «Теория автоматического управления», Балаково 2004