С учетом проведенных преобразований

Используя вычислительную среду MathCAD, получим численное выражение общей передаточной функции системы:

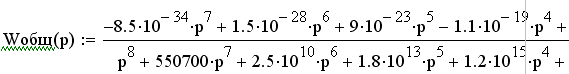
Полученные передаточные функции могут быть использованы для решения широкого круга задач анализа и синтеза. С их помощью можно определить как установившееся значение искомой переменной, так и проводить исследования в частотной и временной областях. Для анализа динамических свойств системы управления рассчитываются переходная и импульсная характеристики.

Одной из основных задач при проектировании системы автоматики является обеспечение её устойчивости. Под устойчивостью понимается свойство системы автоматического управления возвращаться в исходное состояние после вывода её из этого состояния и прекращения влияния задающего или возмущающего воздействия.

1.5 Определение устойчивости линейной системы управления вала дизеля

Исследуем устойчивость системы по критерию Гурвица:

- характеристическое уравнение системы имеет вид:

- выпишем коэффициенты:

a₀=1, а₁=5,5∙10⁵, а₂=2,5∙10¹⁰, а₃=1,8∙10¹³, а₄=1,2∙10¹⁵, а₅=1,4∙10¹⁶,

а₆=6,5∙10¹⁶, а₇=2,3∙10¹⁷, а₈=-7,18∙10¹³

- составим определитель Гурвица, начиная с а₁:

Из главного определителя выделим диагональные миноры и с помощью базы программ системы MathCAD, найдем их численное значение:

> 0;

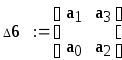
Δ6=1,37∙10¹⁶ >0;

Δ5=2,4∙10²⁹ >0;

Δ4=2,9∙10⁴⁴ >0;

Δ3=3,8∙10⁶⁰ >0;

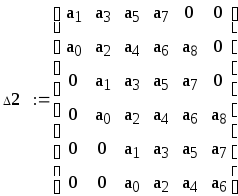
Δ2=1,6∙10⁷⁷ >0;

Δ1=3,8∙10⁹⁴ >0;

Δ=2,7∙10¹⁰⁸ >0

Так как главный определитель и все его диагональные миноры и коэффициент а₀ имеют одинаковый знак и положительны, то система устойчива.

1.6 Построение переходной характеристики линейной системы управления вала дизеля

Переходная функция h(t) представляет собой переходный процесс на выходе системы, возникающий при подаче на её вход скачкообразного воздействия при величине скачка, равного единице.

Для получения изображение переходной функции, то есть зависимости h(t), необходимо выполнить обратное преобразование Лапласа. Задача упрощается ещё больше, если воспользоваться базой программ системы MathCAD.

Переходная функция системы:

Оценить переходный процесс можно по графику переходной функции (рисунок 5).

Рисунок 5 – График переходного процесса линейной системы

1.7 Прямые показатели качества линейной системы

К основным показателям качества, которые определяются по переходной характеристике, относятся:

- установившееся значение:

h_уст= 6,57∙10^-6;

- время переходного процесса системы – это время регулирования системы, определяется как интервал времени от момента приложения какого-либо воздействия на систему до времени вхождения системы в 5% трубку:

t_п = 7.5 сек;

- максимальное значение:

h_мах= 6.57∙10^-6;

- перерегулирование (максимальная динамическая ошибка) – отношения максимального отклонения управляемой переменной относительно её установившегося значения в направлении, противоположном начальному отклонению:

;

- колебательность – число колебаний системы от момента воздействия на неё до перехода в установившееся состояние.

n=0;

- время нарастания регулируемой величины – время, при котором выходная величина достигает своего максимального значения:

t_н=∞;

- время первого согласования – время, за которое регулируемая величина первый раз достигнет своего установившегося значения:

t_c = ∞.

Для того чтобы отследить зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах, обычно строят амплитудо-частотные и фазо-частотные характеристики.

Зависимость разности фаз входных и выходных колебаний от частоты можно просмотреть на фазо-частотной характеристике системы, которая является аргументом амплитудо-фазовой характеристики.

1.8 Косвенные показатели линейной системы

Косвенную оценку качества системы произведём по виду амплитудо-частотной характеристики (рисунок 10).

Амплитудо-частотной характеристикой системы является модуль частотной функции:

Амплитудно-частотная характеристика системы определится следующим выражением, используя функции MathCAD:

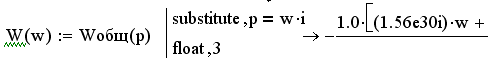
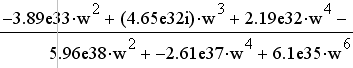
Амплитудно-частотная характеристика приведена на рисунке 6.

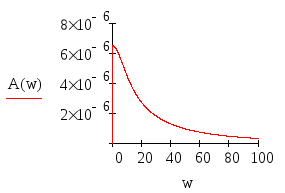
Рисунок 6 – Амплитудно-частотная характеристика

К основным частотным показателям качества систем автоматического управления относятся:

- показатель колебательности:

;

;

;

- резонансная частота – частота, при которой амплитуда достигает значения максимума:

_р=0;

- частота среза определяется как частота, при которой АЧХ принимает значение при А=1, в данном случае ее определить невозможно;

- полоса пропускания частот – интервал частот, когда значения АЧХ больше, чем ;

(₁, ₂) = (0; 12);

- перерегулирование системы:

;

%

Перерегулирование системы является нормальной величиной для функционирования системы автоматического управления вала дизеля, которое должно быть в пределах 10-30%.

Фазо-частотная характеристика системы определится следующим выражением, используя функции MathCAD:

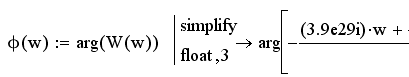
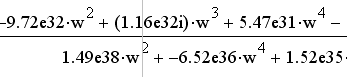
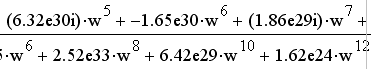
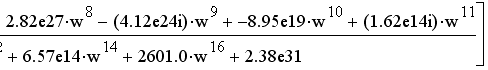
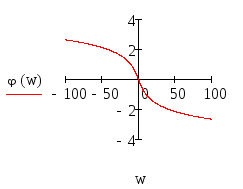
Рисунок 7 - Фазо-частотная характеристика