6.5.1 Спосіб обертання навколо слідів площини (суміщення)

Плоскі фігури можна обертати навколо слідів (як нульових ліній рівня) площини, котрій належать ці фігури, наприклад, для визначення дійсних величин кутів між прямими або для побудови неспотворених зображень плоских фігур. У цьому разі плоска фігура обертається навколо сліду площини, якій належить задана фігура, до суміщення її з якоюсь площиною проекцій. Площина вважається суміщеною з площиною проекцій, якщо побудовано суміщений з цією площиною слід заданої площини. В літературі таке обертання дістало назву суміщення. Розглянемо декілька прикладів.

На рис. 6.21 показано суміщення площини Г(f⁰, h⁰) з горизонтальною площиною проекцій обертанням її навколо горизонтального сліду h⁰. На фронтальному сліді взято точку 1(1₁, 1₂) і обертанням навколо сліду h⁰() побудовано її суміщене положення ₁. Для цього за допомогою прямокутного трикутника О₁1₁1⁰ визначено дійсну довжину О₁1⁰ радіуса обертання точки 1 і за допомогою циркуля відкладено його на перпендикулярі 1₁О₁ до сліду . Маємо точку . Цю точку можна побудувати інакше. Через точку 1₁ провести перпендикуляр до сліду і на ньому зробити засічку радіусом Г_х1₂ із центра Г_х. Через точки Г_х і проведено суміщений з площиною П₁ фронтальний слід . На рис. 6.21 показаний кут α – це дійсна величина кута між слідами f⁰ i h⁰ площини Г.

На рис. 6.22 показано визначення дійсної величини кута між слідами площини Δ(f⁰, h⁰). Цей приклад відрізняється від попереднього лише тим, що кут між слідами площини Δ тупий. Обернемо площину Δ навколо фронтального сліду f⁰(f) до суміщення з фронтальною площиною проекцій П₂ Для цього на сліді h(h, h) візьмімо довільну точку 1(1₁, 1₂) і обернемо її навколо сліду f⁰(f) до суміщення з площиною П₂. Відрізок Г_х1₁ – Рис. 6.21

це неспотворена проекція відрізка Г_х1(Г_х1₁ = Г_х1).

У суміщеному положенні цей відрізок не змінює своєї довжини (Г_х= Г_х1). Проекція 1₂ точки 1 переміщується перпендикулярно до f⁰(f). Тому із точки Г_х як із центра проводимо дугу кола радіусом Г_х1₁ до перетину з перпендикуляром 1₂ до сліду f⁰. Як видно із рис. 6.22 дуга може бути проведеною за годинниковою стрілкою чи проти неї. Отже суміщених положень сліду h⁰ може бути два (на рис. 6.22 показано суцільною тонкою і штриховою). Кут між f і і є дійсною величиною кута між слідами площини Г.

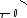Лінії рівня площини, поданої своїми слідами, у суміщеному положенні залишаються паралельними відповідним слідам площини. На рис. 6.23 показано суміщення площини Δ(f⁰, h⁰) з фронтальною площиною проекцій П₂. Суміщений слід побудований за допомогою точки 1(1₁, 1₂), взятої на сліді h⁰(h, h), як це було побудовано на Рис. 6.22

рис. 6.21, 6.22. Через точку 1h⁰

у площині Δ проведена фронталь f(f₁, f₂), а через точку 2f⁰(2₁f, 2₂f) – горизонталь h(h₁, h₂).

У суміщеному положенні площини через точку проведено суміщене положення фронталі паралельно фронтальному сліду f⁰ площини Δ(f₂), а через точку 2₂ – суміщене положення горизонталі паралельно суміщеному положенню горизонтального сліду площини Δ ().

С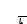лід ще раз звернути увагу на те, що спосіб суміщення є лише різновидом обертання навколо ліній рівня. Різниця полягає лише в тому, що у суміщенні використовуються площини, подані слідами, тобто нульовими лініями рівня, для яких завжди збігаються горизонтальна проекція фронталі з фронтальною проекцією горизонталі.

Наведемо приклад розв’язання, певним чином, зворотної задачі, в якій за заданим неспотвореним зображенням Рис. 6.23

Δ трикутника ABC, що належить

площині (f⁰, h⁰), необхідно побудувати його горизонтальну та фронтальну проекції. Отже, задано зображення Δ трикутника і сліди f⁰(f, f) та h⁰(h, h) площини. Спочатку будуємо суміщене з площиною П₁ зображення фронтального сліду заданої площини. Для цього на сліді f⁰ беремо точку 1(1₁, 1₂) (1₁ f, 1₂f) і обертаємо її навколо горизонталі h⁰ до суміщення з площиною П₁, як це було виконано у попередніх прикладах: 1₁h, Г_х= Г_х1₂. Далі зворотним обертанням навколо горизонталі h⁰(h), будуємо горизонтальну проекціюА₁ вершини А заданого трикутника. Через вершину суміщеного трикутника проводимо допоміжну горизонталь площини  (  h). Через точку проводимо відрізок прямої, перпендикулярної до h, до перетину з проекцією f(2₁  h), а потім за лінією зв’язку знаходимо фронтальну проекцію 2₂ точки 2 і через проекції 2₁ і 2₂ проводимо відповідно горизонтальну і фронтальну проекції допоміжної горизонталі, якій належить вершина А заданого трикутника. За лініями зв’язку будуємо проекції А₁ і А₂ вершини А: A₁  h, A₁A₂  x₁₂.

Cторони і

трикутника продовжуємо Рис. 6.24

до перетину з горизонтальним

слідом h⁰ площини . Маємо точки 3(3₁) і 4(4₁). Під час зворотного обертання площини ці точки залишаються нерухомими. За лініями зв’язку знаходимо їхні фронтальні проекції 3₂ і 4₂ (3₂h, 4₂h). Проекції А₁ і А₂ вершини А сполучаємо відповідно з проекціями 3₁, 4₁ та 3₂, 4₂. Потім за лініями зв’язку будуємо проекції B₁, B₂ та C₁, C₂ вершин В і С: В₁А₁3₁, В₂А₂3₂; С₁А₁4₁, С₂А₂4₂.

Як видно з рис. 6.24, варіантів побудов проекцій А₁, А₂, В₁, В₂, С₁, С₂ вершин трикутника АВС може бути декілька як за послідовністю цих побудов, так і за допоміжними прямими, які використовуються для побудов, тобто кожна з вершин ΔАВС може бути побудована за допомогою горизонталі, фронталі чи будь-якої прямої загального положення площини .