§36. Рух мікрочастинки в нескінченно глибокій одновимірній потенціальній ямі. Проходження частинки через потенціальний бар’єр

У

Рис.1

сякий зв’язаний стан частинки (вільний електрон в металі, нуклон в ядрі тощо), тобто стан з від’ємною потенціальною енергією, можна описати, ввівши поняття потенціальної ями. Розглянемо найпростіший випадок, коли частинка масою m перебуває в одновимірній прямокутній нескінченно глибокій потенціальній ямі шириною (рис. 1). Оператор Гамільтона для цього випадку має вигляд

,

де

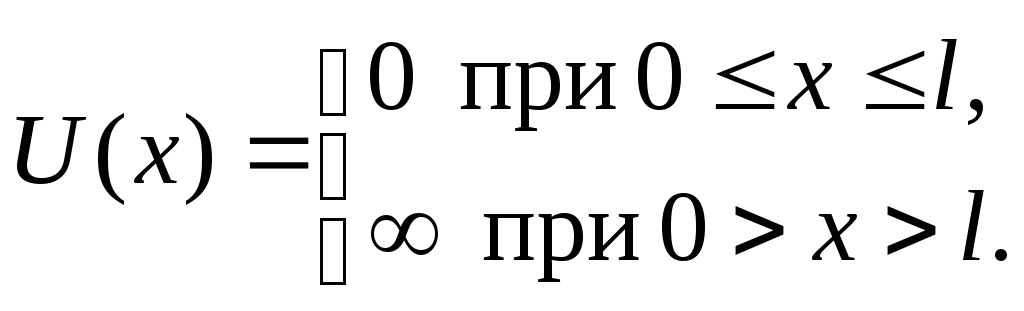
Всередині ящика рівняння Шредінгера запишеться як

або

. (1)

Введемо позначення

, (2)

де k має зміст хвильового числа. Тоді рівняння (2) набуде форми, подібної до диференціального рівняння гармонічних коливань,

.

Розв’язок цього рівняння шукаємо у вигляді гармонічної функції координати х:

. (3)

Оскільки хвильова функція повинна бути неперервною, в тому числі і на стінках ями, а вийти за межі ями частинка не може, то . Перша гранична умова дає , і тому

. (4)

Друга гранична умова дає

, де n = 1, 2, 3, … – квантове число стану частинки (5)

Врахувавши, що , отримаємо з (5) співвідношення , тобто в межах ширини ями повинно вкладатись ціле число півхвиль де Бройля.

Формальну амплітуду А в (4) знайдено з умови нормування хвильової функції до одиниці:

.

Звідси , і остаточно хвильова функція частинки в довільному квантовому стані n, з врахуванням (5), набуває вигляду

. (6)

Об’єднуючи (2) і (5), отримаємо вираз для енергії частинки в різних квантових станах

. (7)

Отже, енергія частинки в потенціальній ямі приймає не довільні, а дискретні значення Е₁, Е₂, Е₃, …, зображені на рис.1 відповідними енергетичними рівнями. Густина імовірності (на рисунку – штрихові лінії) залежить від координати частинки, при цьому по різному в кожному квантовому стані. Наприклад, для центру ями вона максимальна в стані n = 1 і дорівнює нулю в стані n = 2.

Відстань між сусідніми енергетичними рівнями

. (8)

Р

Рис. 2

озглядаючи електрон в атомі як такий, що перебуває в потенціальній ямі шириною , отримаємо , що співмірно з енергією електрона. В цей же час в макросвіті, коли m i l – дуже великі, відстань між енергетичними рівнями стає зникаюче малою, і квантуванням енергії можна знехтувати.

Задача про частинку в потенціальній ямі скінченої глибини розв’язується значно складніше, але висновок про квантування енергії і в цьому випадку залишається в силі.

Спорідненою до описаної є задача про проходження частинки через потенціальний бар’єр. Нехай мікрочастинка з масою m і енергією Е налітає на одновимірний прямокутний потенціальний бар’єр шириною l і висотою U₀ (рис. 2). Якщо частинка класична, то вона пролітає над бар’єром, коли Е > U₀, і відбивається від нього, коли Е < U₀. Проникнути під бар’єр класична частинка не може, бо тоді її кінетична енергія була б меншою від нуля. Розв’язок рівняння Шредінгера для квантомеханічної мікрочастинки дає, що хвильові функції в усіх трьох областях відмінні від нуля, тобто мікрочастинка проникає під бар’єр і за бар’єр. Це явище називається тунелюванням. Від’ємні значення кінетичної енергії мікрочастинки в момент проходження бар’єру не можуть турбувати, бо в квантовій механіці кінетична енергія , як і потенціальна енергія, не є точно визначеними. Прозорість бар’єру, тобто імовірність тунелювання частинки, знаходиться як відношення густин імовірності в областях ІІІ та І. Розрахунок дає

. (9)

Звідси видно , що бар’єр тим прозоріший, чим менші його ширина і висота. Для класичної частинки (m  ) і макробар’єру (l  ) прозорість бар’єру зникаюче мала.